 |
Сила притяжения между двумя разноименно заряженными обкладками конденсатора
|
|
|
|
Сила притяжения между двумя разноименно заряженными обкладками конденсатора
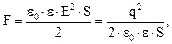
где S – площадь пластин.
Электроемкость:
а) уединенного проводника
C = q/φ;
г) шара
С = 4π ε ε 0r,
где r - радиус шара.
б) плоского конденсатора
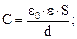
в) слоистого конденсатора
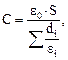
где d – расстояние между пластинами конденсатора; di – толщина i-го слоя диэлектрика; ε i – его диэлектрическая проницаемость.
Электроемкость батареи конденсаторов, соединенных:
а) параллельно
C = Σ Ci
б) последовательно
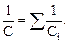
Энергия поля:
а) заряженного проводника
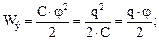
б) заряженного конденсатора
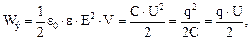
где V – объем конденсатора.
Объемная плотность энергии электрического поля
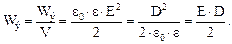
Примеры решения задач
Пример 1. Движение тела массой 1 кг задано уравнением
s = 6∙ t3 + 3∙ t + 2. Найти зависимость скорости и ускорения от времени. Вычислить силу, действующую на тело в конце второй секунды.
Решение. Мгновенную скорость находим как производную пути от времени:
υ = ds/dt; υ = 18∙ t2 + 3.
Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени:
a = dυ /dt = d2s/dt2; a = 36∙ t.
Сила, действующая на тело, определяется по второму закону Ньютона: F = m∙ a, где а, согласно условию задачи, – ускорение в конце второй секунды. Тогда
F = m∙ 36∙ t; F = 1 кг∙ 36∙ 2 м/с2 = 72 Н.
Ответ: υ = 18∙ t2 + 3; a = 36∙ t; F = 72 Н.
Пример 2. Тело вращается вокруг неподвижной оси по закону
φ = A + Bt + Ct2, где А = 10 рад, В = 20 рад/с, С = -2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r = 0, 1 м от оси вращения, для момента времени t = 4 c.
Решение. Полное ускорение 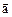 точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения
точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения 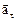 , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения  , направленного к центру кривизны траектории (см. рис. ):
, направленного к центру кривизны траектории (см. рис. ):
|
|
|
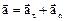 .
.
 Так как векторы
Так как векторы 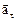 и
и  взаимно перпендикулярны, то модуль ускорения
взаимно перпендикулярны, то модуль ускорения
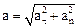 . (1)
. (1)
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами:
аτ = ε ∙ r; аn = ω 2∙ r,
где ω – модуль угловой скорости тела; ε – модуль его углового ускорения.
Подставляя выражения аτ и аn в формулу (1), находим:
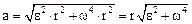 . (2)
. (2)
Угловую скорость ω найдем, взяв первую производную угла поворота по времени:
ω = dφ /dt = B + 2C∙ t.
В момент времени t = 4c модуль угловой скорости
ω = [20 + 2(-2)4] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:
ε = dω /dt = 2C = -4 рад/с2.
Подставляя значения ω, ε и r в формулу (2), получаем
а = 0, 1 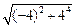 м/с2 = 1. 65 м/с2.
м/с2 = 1. 65 м/с2.
Ответ: а = 1. 65 м/с2.
Пример 3. Ящик массой m1 = 20 кг соскальзывает по идеально гладкому лотку длиной l = 2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2 = 80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость u тележки с ящиком, если лоток наклонен под углом α = 300 к рельсам.
Решение. Тележку и ящик можно рассматривать как систему двух неупруго взаимодействующих тел. Но эта система не замкнута, так как на нее действуют внешние силы: силы тяжести m1g и m2g и сила реакции N2 (см. рис. ). Поэтому применить закон сохранения импульса к системе ящик – тележка нельзя. Но так как проекции указанных выше сил на направление оси х, совпадающей с направлением рельсов, равны нулю, то проекцию импульса системы на это направление можно считать постоян
 |
ной,
т. е.
р1х + р2х = р'1х + р'2х, (1)
где р1х и р2х – проекции импульса ящика и тележки с песком в момент падения ящика на тележку; р'1х и р'2х – те же величины после падения ящика.
|
|
|
Рассматривая тела системы как материальные точки, выразим в равенстве (1) импульсы тел через их массы и скорости, учитывая, что р2х = 0 (тележка до взаимодействия с ящиком покоилась), а также что после взаимодействия оба тела системы движутся с одной и той же скоростью u:
m1υ 1x = (m1 + m2)∙ u
или
m1υ 1∙ cos α = (m1 + m2)∙ u,
где υ 1 – модуль скорости ящика перед падением на тележку; υ 1x = υ 1∙ cos α – проекция этой скорости на ось х.
Отсюда u = m1υ 1∙ cos α /(m1 + m2). (2)
Модуль скорости υ 1 определим из закона сохранения энергии:
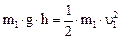 ,
,
где h = l∙ sin α, откуда
 .
.
Подставив выражение для υ 1 в формулу (2), получим:
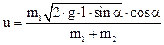 .
.
После вычислений найдем:
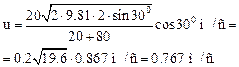
Ответ: u = 0. 767 м/с.
 Пример 4. На спокойной воде пруда перпендикулярно берегу и носом к нему стоит лодка массой М и длиной L. На корме стоит человек массой m. На какое расстояние s удалится лодка от берега, если человек перейдет с кормы на нос лодки? Силами трения и сопротивления пренебречь.
Пример 4. На спокойной воде пруда перпендикулярно берегу и носом к нему стоит лодка массой М и длиной L. На корме стоит человек массой m. На какое расстояние s удалится лодка от берега, если человек перейдет с кормы на нос лодки? Силами трения и сопротивления пренебречь.
Решение. Систему человек – лодка относительно горизонтального направления можно рассматривать как замкнутую. Согласно следствию из закона сохранения импульса внутренние силы замкнутой системы не могут изменить положение центра масс системы. Применяя это следствие к системе человек – лодка, можно считать, что при перемещении человека по лодке центр масс системы не изменит своего положения, т. е. останется на прежнем расстоянии от берега.
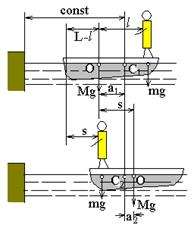
Пусть центр масс системы человек – лодка находится на вертикали, проходящей в начальный момент через точку С1 лодки (см. рис. ), а после перемещения лодки – через другую ее точку С2. Так как эта вертикаль неподвижна относительно берега, то искомое перемещение s лодки относительно берега равно перемещению лодки относительно вертикали. А это последнее легко определить по перемещению центра масс О лодки.
Как видно из рисунка, в начальный момент точка О находится на расстоянии а1 слева от вертикали, а после перехода человека – на расстоянии а2 справа от вертикали. Следовательно, искомое перемещение лодки
s = a1 + a2.
Для определения а1 и а2 воспользуемся тем, что результирующий момент сил, действующих на систему относительно горизонтальной оси, перпендикулярной продольной оси лодки, равен нулю. Поэтому для начального положения системы
|
|
|
M∙ g∙ a1 = m∙ g∙ (l – a1), откуда
а1 = m∙ l/(M + m).
После перемещения лодки M∙ g∙ d2 = m∙ g∙ (L – d2 – l), откуда
a2 = m(L – l)/(M + m).
Подставив полученные выражения а1 и а2 в (1), найдем
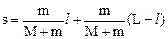 , или
, или  .
.
Пример 5. На двух шнурах одинаковой длины l = 0. 8 м, подвешены два свинцовых шара массами m1 = 0. 5 кг и m2 = 1 кг. Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол α = 600, и отпустили. На какую высоту h поднимутся оба шара после столкновения? Удар считать центральным и неупругим. Определить энергию Δ E, израсходованную на деформацию шара при ударе.
Решение. Так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью υ. Закон сохранения количества движения при этом ударе имеет вид:
m1∙ υ 1 + m2∙ υ 2 = (m1 + m2)∙ υ. (1)
Здесь υ 1 и υ 2 – скорости шаров до удара. Скорость большего шара до удара равна нулю (υ 2 = 0). Скорость меньшего шара найдем, используя закон сохранения энергии. При отклонении меньшего шара на угол α ему сообщается потенциальная энергия, которая затем переходит в кинетическую: m1∙ g∙ h1 = m1∙ υ 12/2. Т. к. h1 = = l(1_– cos α ) = 2∙ l∙ sin2(α /2), то
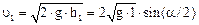 . (2)
. (2)
Из уравнений (1) и (2) находим скорость шаров после удара:
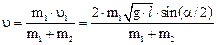 . (3)
. (3)
Кинетическая энергия, которой обладают шары после удара, переходит в потенциальную:
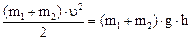 ,
,
где h – высота поднятия шаров после столкновения. Из формулы (4) находим h = υ 2/(2∙ g), или с учетом (3):
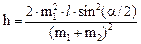 ;
;
h = 2(0. 5 кг)2∙ 0. 8 м∙ 0. 25/(0. 5 кг + 1 кг)2 = 0. 044 м
При неупругом ударе шаров часть энергии расходуется на их деформацию. Энергия деформации определяется разностью кинетических энергий до и после удара:
 .
.
Используя уравнения (2) и (3), получаем:
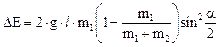 ;
;
Проверим, дает ли полученная формула единицу энергии:
[g]∙ [l]∙ [m] = 1 м/с2∙ 1 м∙ 1 кг = 1 Дж.
Δ E = 2∙ 9. 81 м/с2∙ 0. 8 м∙ 0. 5 кг (1 – 0. 5 кг/1, 5 кг)∙ 0. 25 = 1. 3 Дж.
Ответ: Δ E = 1. 3 Дж.
|
|
|
Пример 6. Молот массой m1 = 70 кг падает с высоты h = 5 м и ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием m2 = 1330 кг. Считая удар абсолютно неупругим, определить энергию E, расходуемую на деформацию изделия. Систему молот – изделие – наковальня считать замкнутой.
Решение. По условию задачи система молот – изделие – наковальня считается замкнутой, а удар неупругий. На основании закона сохранения энергии можно считать, что энергия, затраченная на деформацию изделия, равна разности значений механической энергии системы до и после удара.
Считаем, что во время удара изменяется только кинетическая энергия тел, т. е. незначительным перемещением тел по вертикали во время удара пренебрегаем. Тогда для энергии деформации изделия имеем:
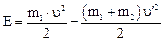 , (1)
, (1)
где υ – скорость молота в конце падения с высоты h; υ ' – общая скорость всех тел системы после неупругого удара. Скорость молота в конце падения с высоты h определяется без учета сопротивления воздуха и трения по формуле:
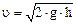 . (2)
. (2)
Общую скорость всех тел системы после неупругого удара найдем, применив закон сохранения количества движения:
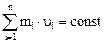 . (3)
. (3)
Для рассматриваемой системы закон сохранения количества движения имеет вид m1∙ υ = 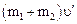 , откуда
, откуда
υ ' = m1∙ υ /(m1 + m2). (4)
Подставив в формулу (1) выражения (2) и (4), получим:
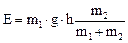 ;
;
Е = 70 кг ∙ 9. 8 м/с2 ∙ 5 м ∙ (1330 кг/(1330 кг + 70 кг)) = 3258 Дж.
Ответ: Е = 3258 Дж.
Пример 7. При выстреле из пружинного пистолета вертикально вверх пуля массой m = 20 г поднялась на высоту h = 5 м. Определить жесткость k пружины пистолета, если она была сжата на х = 10 см. Массой пружины и силами трения пренебречь.
Решение. Рассмотрим систему пружина – пуля. Так как на тела системы действуют только консервативные силы, то для решения задачи можно применить закон сохранения энергии в механике. Согласно ему полная механическая энергия Е1 системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии Е2 в конечном состоянии (когда пуля поднялась на высоту h), т. е.
Е1 = Е2, или Е1к + Е1п = Е2к + Е2п, (1)
где Е1к, Е2к, Е1п, Е2п – кинетические и потенциальные энергии системы в начальном и конечном состояниях.
Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид:
Е1п = Е2п. (2)
Примем потенциальную энергию пули в поле сил тяготения Земли, когда пуля покоится на сжатой пружине, равной нулю, а высоту подъема пули будем отсчитывать от торца сжатой пружины. Тогда энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т. е. Е1п = k∙ x2/2, а в конечном состоянии – потенциальной энергии пули на высоте h, т. е. Е2п = m∙ g∙ h.
|
|
|
Подставив выражения Е1п и Е2п в формулу (2), найдем
k∙ x2/2 = m∙ g∙ h, откуда
k = 2 m∙ g∙ h/x2.
Подставив в формулу (3) значения величин и размерностей, произведем вычисления:
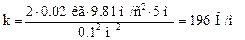
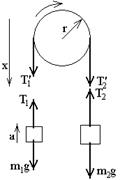 Ответ: k = 196 Н/м.
Ответ: k = 196 Н/м.
Пример 8. Через блок в виде сплошного диска, имеющего массу m = 80 г (см. рис. ), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m1 = 100 г и m2 = 200 г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.
Решение. Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза
m1∙ g – T1 = – m1∙ a; (1)
для второго груза
m2∙ g – T2 = m2∙ a. (2)
Под действием моментов сил Т1' и Т2' относительно оси z, перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение ε. Согласно основному уравнению динамики вращательного движения
Т2'∙ r – Т1'∙ r = Jz∙ ε, (3)
где ε = a/r; Jz = m∙ r2/2 – момент инерции блока (сплошного диска) относительно оси z.
Согласно третьему закону Ньютона с учетом невесомости нити Т1' = Т1, Т2' = Т2. Воспользовавшись этим, подставим в уравнение (3) вместо Т1' и Т2' выражения Т1 и Т2, получив их предварительно из уравнений (1) и (2):
(m1∙ g – m2∙ a)∙ r – (m1∙ g + m1∙ a)∙ r = m∙ r2∙ a/(2∙ r).
После сокращения на r и перегруппировки членов найдем:
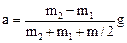 .
.
Формула (4) позволяет массы m1, m2 и m выразить в граммах, как они даны в условии задачи, а ускорение в единицах СИ. После подстановки числовых значений и размерностей в формулу (4) получим:
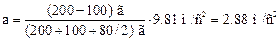
Ответ: а = 2. 88 м/с2.
Пример 9. Маховик массой m = 4 кг вращается с частотой n = 720 мин-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика можно считать равномерно распределенной по его ободу радиусом R = 40 см. Через Δ t = 30 с под действием тормозящего момента маховик остановился. Найти тормозящий момент М и число оборотов N, которое сделает маховик до полной остановки.
Решение. Для определения тормозящего момента М сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения:
J∙ Δ ω = M∙ Δ t, (1)
где J – момент инерции маховика относительно оси, проходящей через центр масс; Δ ω – изменение угловой скорости за промежуток времени Δ t.
По условию Δ ω = –ω 0, где ω 0 – начальная угловая скорость, так как конечная угловая скорость ω = 0. Выразим начальную угловую скорость через частоту вращения маховика; тогда ω 0 = 2π ∙ n и Δ ω = 2π ∙ n. Момент инерции маховика J = m∙ R2, где m – масса маховика; R – его радиус. Формула (1) принимает вид:
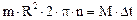 ,
,
откуда
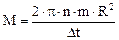 ;
;
М = 2∙ 3, 14∙ 12 с-1∙ 4 кг∙ 0, 16 м2с-2/30 с = 1, 61 Н∙ м.
Угол поворота (т. е. угловой путь φ ) за время вращения маховика до остановки может быть определен по формуле для равнозамедленного вращения:
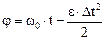 (2)
(2)
где ε – угловое ускорение. По условию ω = ω 0 – ε ∙ Δ t, ω = 0,
ε ∙ Δ t = ω 0. Тогда выражение (2) можно записать так:
φ = ω 0∙ Δ t – ω 0∙ Δ t/2 = ω 0∙ Δ t/2.
Так как φ = 2∙ π ∙ N, ω 0 = 2∙ π ∙ n, то число полных оборотов
N = n∙ Δ t/2; N = 12 c-1 ∙ (30 c)/2 = 180.
Ответ: N = 180.
Пример 10. Платформа в виде сплошного диска радиусом
R = 1. 5 м и массой m1 = 180 кг вращается около вертикальной оси с частотой n = 10 мин-1. В центре платформы стоит человек
m2 = 60 кг. Какую линейную скорость υ относительно пола помещения будет иметь человек, если он перейдет на край платформы?
Решение. Согласно условию задачи момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция Lz момента импульса системы платформа-человек остается постоянной:
Lz = Jz∙ ω = const, (1)
где Jz – момент инерции платформы с человеком относительно оси z; ω – угловая скорость платформы.
Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому в начальном состоянии Jz = J1 + J2, а в конечном состоянии J'z = J'1 + J'2.
С учетом этого равенство (1) примет вид:
(J1 + J2)∙ ω = (J'1 + J'2)∙ ω ', (2)
где значения моментов инерции J1 и J2 платформы и человека соответственно относятся к начальному состоянию системы; J'1 и J'2 – к конечному.
Момент инерции платформы относительно оси z при переходе человека не изменяется: J1 = J'1 = m1∙ R2/2. Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J2 в начальном состоянии (в центре платформы) можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека J'2 = m2∙ R2.
Подставим в формулу (2) выражения моментов инерции, начальной угловой скорости вращения платформы с человеком (ω = 2∙ π ∙ n) и конечной угловой скорости (ω ' = υ /R, где υ – скорость человека относительно пола):
(m1∙ R2/2 + 0) 2∙ π ∙ n = (m1∙ R2/2 + m2∙ R2)∙ υ /R.
После сокращения на R2 и простых преобразований находим скорость:
υ = 2∙ π ∙ n∙ R∙ m1/(m1 + 2∙ m2).
Произведем вычисления:
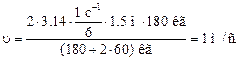
Ответ: υ = 1 м/с.
Пример 11. Стержень длиной l = 1. 5 м и массой М = 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня (см. рис. ). В середину стержня ударяет пуля массой m = 10 г, летящая в горизонтальном направлении со скоростью υ 0 = 500 м/с, и застревает в стержне. На какой угол φ отклонится стержень после удара?
Решение. Удар пули следует рассматривать как неупругий: после удара и пуля, и соответствующая точка стержня будут двигаться с одинаковыми скоростями. В момент удара на пулю и на стержень действуют силы тя 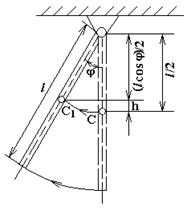 жести, линии действия которых проходят через ось вращения и направлены вертикально вниз. Моменты этих сил относительно оси вращения равны нулю. Поэтому при ударе пули о стержень будет справедлив закон сохранения импульса.
жести, линии действия которых проходят через ось вращения и направлены вертикально вниз. Моменты этих сил относительно оси вращения равны нулю. Поэтому при ударе пули о стержень будет справедлив закон сохранения импульса.
В начальный момент удара угловая скорость стержня
ω 0 = 0, поэтому его момент им-пульса L01 = J∙ ω 0 = 0. Начальный момент импульса пули
L02 = m∙ υ 0∙ r, где r – расстояние от точки попадания до оси вращения. В конечный момент удара стержень имел угловую скорость ω, а пуля – линейную скорость υ, равную линейной скорости точек стержня, находящихся на расстоянии r от оси вращения. Так как υ = ω ∙ r, то конечный момент импульса пули L2 = m∙ υ ∙ r = m∙ r2∙ ω.
Применив закон сохранения импульса, можем написать:
L01 + L02 = L1 + L2 или m∙ υ 0∙ r = J∙ ω + m∙ r2∙ ω,
откуда

где J = M∙ l2/3 – момент инерции стержня. Отсюда получим:
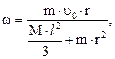 (1)
(1)
Кинетическая энергия стержня после удара равна:
Ек = J∙ ω 2/2, (2)
Затем стержень поворачивается на искомый угол φ, причем центр масс его С поднимается на высоту h = (l/2)∙ (1 – cosφ ). В отклоненном положении стержень будет обладать потенциальной энергией, равной
Еп = M∙ g∙ (l/2)∙ (1 – cosφ ). (3)
Потенциальная энергия получена за счет кинетической энергии и равна ей по закону сохранения энергии. Приравняв правые части равенств (2) и (3), получим:
M∙ g∙ (l/2)∙ (1 – cosφ ) = J∙ ω 2/2.
Отсюда
cosφ = 1 – J∙ ω 2/( M∙ g∙ l).
Подставив в эту формулу выражение для момента инерции стержня J = M∙ l2/3, получим
cosφ = 1 – l∙ ω 2/(3∙ g). (4)
Подставив значение ω = 0, 5 рад/с, найденной из (1), получим
cosφ = 0. 987; φ = 9020'.
Ответ: ω = 0. 5 рад/с; cosφ = 0. 987; φ = 9020'.
Пример 12. Точка совершает гармонические колебания с частотой ν = 10 Гц. В момент, принятый за начальный, точка имела максимальное смещение хmax = 1 мм. Написать уравнение колебаний точки и начертить их график.
Решение. Уравнение колебаний точки можно записать в виде:
x = A∙ sin(ω t + φ 1), (1)
где А – амплитуда колебаний; ω – циклическая частота; t – время; φ 1 – начальная фаза.
По определению амплитуда колебаний
А = хmax. (2)
Циклическая частота ω связана с частотой ν соотношением:
ω = 2∙ π ∙ ν. (3)
Для момента времени t = 0 формула (1) примет вид:
хmax = A∙ sinφ 1
откуда начальная фаза
φ 1 = arcsin(хmax/A) = arcsin 1,
или
φ 1 = (2k + 1)∙ π /2 (k = 0, 1, 2, …)
Изменение фазы на 2π не изменяет состояния колеблющейся точки, поэтому можно принять
φ 1 = π /2. (4)
С учетом равенств (2)-(4) уравнение колебаний примет вид
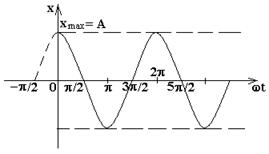
x = A∙ sin(2∙ π ∙ ν ∙ t + φ 1), или x = A∙ cos(2∙ π ∙ ν ∙ t),
где А = 1 мм = 10-3 м, ν = 10 Гц, φ 1 = π /2.
График соответствующего гармонического колебания приведен на рис.
 |
Пример 13. Частица массой m = 0. 01 кг совершает гармонические колебания с периодом Т = 2 с. Полная энергия колеблющейся частицы Е = 0. 1 мДж. Определить амплитуду А колебаний и наибольшее значение силы Fmax, действующей на частицу.
Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:

где ω = 2∙ π /Т. Отсюда амплитуда
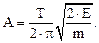 (1)
(1)
Проверим размерности:
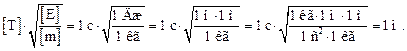
Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F = -k∙ x, где k – коэффициент квазиупругой силы; х – смещение колеблющейся точки. Максимальная сила будет при максимальном смещении хmax, равном амплитуде:
Fmax = k∙ A. (2)
Коэффициент k выразим через период колебаний:
k = m∙ ω 2 = m∙ 4∙ π 2/T2. (3)
Подставив выражения (1) и (3) в (2) и произведя упрощения, получим:
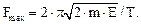
Произведем вычисления:
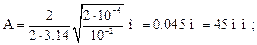
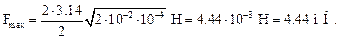
Проверим размерность:
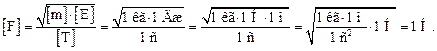
Ответ: А = 45 мм; Fmax = 4. 44 мН.
Пример 14. В баллоне объемом 10 л находится гелий под давлением р1 = 1 МПа и при температуре Т1 = 300 К. После того как из баллона было взято m = 10 г гелия, температура в баллоне понизилась до Т2 = 290 К. Определить давление р2 гелия, оставшегося в баллоне.
Решение. Для решения задачи воспользуемся уравнением Менделеева – Клапейрона, применив его к конечному состоянию газа:
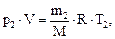 (1)
(1)
где m2 – масса гелия в баллоне в конечном состоянии; M – молярная масса гелия; R – молярная газовая постоянная.
Из уравнения (1) выразим искомое давление:
 (2)
(2)
Массу m2 гелия выразим через массу m1, соответствующую начальному состоянию, и массу m гелия, взятого из баллона:
m2 = m1 – m. (3)
Массу m1 гелия найдем также из уравнения Менделеева – Клапейрона, применив его к начальному состоянию:
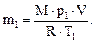 (4)
(4)
Подставив выражение для массы m1 в (3), а затем выражение для m2 в (2), найдем
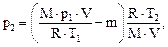
или
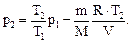 (5)
(5)
Проверим, дает ли формула (5) единицу давления. Для этого в ее правую часть вместо символов величин подставим их единицы:
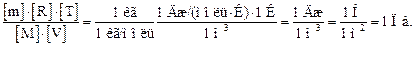
Произведем вычисления по формуле (5), учитывая, что М = 4∙ 10-3 кг/моль (см. табл. Приложения):
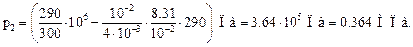
Ответ: р2 = 0. 364 МПа.
Пример 15. В сосуде объемом V = 2 м3 находится смесь m1 = 4 кг гелия и m2 = 2 кг водорода при температуре T = 270С. Определить давление p и молярную массу M смеси газов.
Решение. Воспользуемся уравнением Менделеева – Клапейрона, применив его к гелию и водороду:
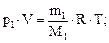 (1)
(1)
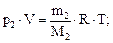 (2)
(2)
где р1 – парциальное давление гелия; М1 – молярная масса гелия; R = 8. 31 Дж/(моль∙ К) – молярная газовая постоянная; р2 – парциальное давление водорода; М2 – его молярная масса.
Под парциальным давлением р1 и р2 понимается то давление, которое производил бы газ, если бы он только один находился в сосуде. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси:
р = р1 + р2. (3)
Из уравнения (1) и (2) выразим р1 и р2 и подставим в уравнение (3). Имеем:
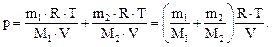 (4)
(4)
Молярную массу смеси газов найдем по формуле:
 (5)
(5)
где ν 1 и ν 2 – число молей гелия и водорода соответственно.
Число молей газов определим по формулам:
ν 1 = m1/M1; (6)
ν 2 = m2/M2; (7)
Подставляя (6) и (7) в (5), найдем
 (8)
(8)
Подставляя числовые значения в формулы (4) и (8), получаем
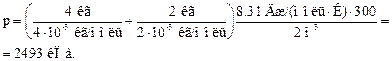
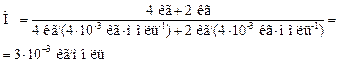
Ответ: р = 2493 кПа, М = 3∙ 10-3 кг/моль.
Пример 16. Чему равны средние кинетические энергии поступательного < ε пост> и вращательного < ε вр> движения молекул, содержащихся в m = 2 кг водорода при температуре T = 400 К?
М = 2∙ 10-3 кг/моль.
Решение. Считаем водород идеальным газом. Молекула водорода – двухатомная, связь между атомами считаем жесткой. Тогда число степеней свободы молекулы водорода равно 5. В среднем на одну степень свободы приходится энергия < ε 1> = k∙ T/2, где k – постоянная Больцмана; Т – термодинамическая температура. Поступательному движению приписывается три (i = 3), а вращательному две (i = 2) степени свободы. Энергия одной молекулы
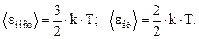
Число молекул, содержащихся в массе газа m,
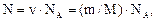
где ν – число молей; NA – постоянная Авогадро. Тогда средняя кинетическая энергия поступательного движения молекул водорода
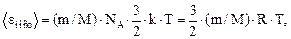 (1)
(1)
где R = k∙ NA – молярная газовая постоянная.
Средняя кинетическая энергия вращательного движения молекул водорода
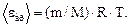 (2)
(2)
Подставляя числовые значения в формулы (1) и (2), имеем
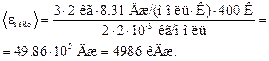
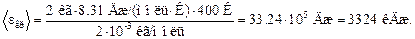
Ответ: 
Пример 17. Вычислить удельные теплоемкости при постоянном объеме сv и при постоянном давлении ср неона и водорода, принимая эти газы за идеальные.
Решение. Удельные теплоемкости идеальных газов выражаются формулами:
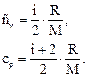
где i – число степеней свободы молекулы газа; М – молярная масса. Для неона (одноатомный газ) i = 3 и М = 20∙ 10-3 кг/моль (см. табл. Приложения).
Произведем вычисления:
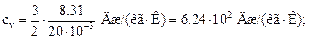

Для водорода (двухатомный газ) i =5 и М = 2∙ 10-3 кг/моль. Тогда
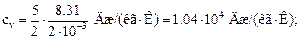
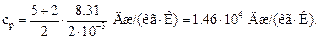
Ответ: для неона сv = 6. 24∙ 102 Дж/(кг∙ К); ср = 1. 04∙ 103 Дж/(кг∙ К);
для водорода сv = 1. 04∙ 104 Дж/(кг∙ К); ср = 1. 46∙ 104 Дж/(кг∙ К).
Пример 18. Вычислить удельные теплоемкости сv и ср смеси неона и водорода, если массовые доли неона и водорода составляют ω 1 = 80% и ω 2 = 20%. Значения удельных теплоемкостей газов взять из предыдущего примера.
Решение. Удельную теплоемкость сv смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на Δ Т, выразим двумя способами:
Q = сv∙ (m1 + m2)∙ Δ T; (1)
Q = (сv1∙ m1 + сv2∙ m2)∙ Δ T, (2)
где сv1 – удельная теплоемкость неона; сv2 – удельная теплоемкость водорода.
Приравняв правые части (1) и (2) и разделив обе части полученного равенства на Δ T, получим сv∙ (m1 + m2) = сv1∙ m1 + сv2∙ m2. Отсюда
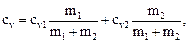
или сv = cv1∙ ω 1 + cv2∙ ω 2,
где ω 1 = m1/(m1 + m2) и ω 2 = m2/(m1 + m2).
Рассуждая так же, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:
ср = cр1∙ ω 1 + cр2∙ ω 2.
Произведем вычисления:
cv = (6. 24∙ 102∙ 0. 8 + 1. 04∙ 104∙ 0. 2) Дж/(кг∙ К) =
= 2. 58∙ 103 Дж/(кг∙ К) = 2. 58 кДж/(кг∙ К);
ср = (1. 04∙ 103∙ 0. 8 + 1. 46∙ 104∙ 0. 2) Дж/(кг∙ К) =
= 3. 75∙ 103 Дж/(кг∙ К) = 3. 75 кДж/(кг∙ К).
Ответ: cv = 2. 58 кДж/(кг∙ К); ср = 3. 75 кДж/(кг∙ К).
Пример 19. Определить среднюю длину свободного пробега молекул 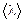 и число соударений Z за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью
и число соударений Z за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью
V = 2 л при температуре t = 270С и давлении p = 100 кПа. M = 32∙ 10-3 кг/моль; d = 2. 9∙ 10-10 м.
Решение. Средняя длина свободного пробега молекул идеального газа вычисляется по формуле:
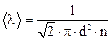 , (1)
, (1)
где d – эффективный диаметр молекулы газа; n – число молекул в единице объема, которое можно определить из уравнения:
n = p/(k∙ T), (2)
где k – постоянная Больцмана. Подставляя (2) в (1), имеем
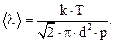 (3)
(3)
Число соударений Z, происходящих между всеми молекулами за 1 с, равно
Z = 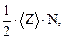 (4)
(4)
где N – число молекул кислорода в сосуде объемом 2∙ 10-3 м3;  – среднее число соударений одной молекулы за 1 с. Число молекул в сосуде
– среднее число соударений одной молекулы за 1 с. Число молекул в сосуде
N = n∙ V. (5)
Среднее число соударений молекулы за 1 с равно:
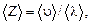 (6)
(6)
где 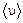 – средняя арифметическая скорость молекулы
– средняя арифметическая скорость молекулы
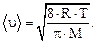 (7)
(7)
Подставляя в (4) выражения (5), (6) и (7), находим:

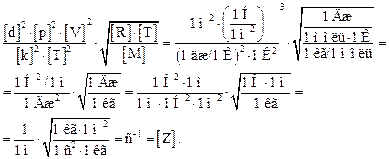 |
Проверим размерности:
Подставляя числовые значения, получим:
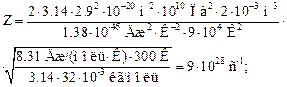
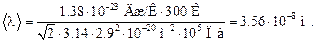
Ответ: Z = 9∙ 1028 c-1, < λ > = 3. 56∙ 10-8 м.
Пример 20. Определить коэффициенты диффузии D и внутреннего трения η азота, находящегося при тем
|
|
|


