По количеству измерительной информации

Однократные измерения – это одно измерение одной величины. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями, поэтому следует проводить не менее трех однократных измерений и находить конечный результат как среднее арифметическое значение.

Многократные измерения позволяют получить результат из нескольких следующих друг за другом измерений одного и того же объекта. Обычно минимальное число измерений в данном случае больше трех..

По отношению к основным единицам Абсолютные измерения основаны на прямых измерениях основ­ных величин и использовании значений физических констант (на­пример, измерение длины штангенциркулем).

При относительных измерениях величину сравнивают с одноименной, играющей роль еди­ницы или принятой за исходную. Примером относительного изме­рения является измерение диаметра вращающейся детали по числу оборотов соприкасающегося с ней аттестованного ролика.

Метрологические характеристики средств измерений.

При оценке возможностей любого средства измерений (СИ) необходимо знать его основные мет-

рологические характеристики. К ним относятся:

а) диапазон измерений — область значений измеряемой величины с нормированными допускае-

мыми погрешностями СИ;

б) пределы измерений – наименьшее и наибольшее значения диапазона измерений;

в) порог чувствительности – наименьшее изменение измеряемой величины, которое вызывает за-

метное изменение выходного сигнала;

г) погрешность средства измерений – это разность между показаниями СИ и истинным (действи-

тельным) значением измеряемой величины.

д) точность измерений – характеристика качества измерений, отражающая близость к нулю по-

грешностей их результатов.

Метрологические характеристики СИ с отсчетными устройствами, содержащими одну или не-

сколько шкал:6

е) длина деления шкалы – расстояние между осями (центрами) двух соседних отметок шкалы, и замеренное вдоль воображаемой линии, проходящей через середины самых коротких отметок шкалы;

ж) цена деления шкалы – разность значений величины, соответствующих двум соседним отметкам

шкалы;

з) диапазон показаний (измерений по шкале) – область значений шкалы, ограниченная начальным и конечным значениями шкалы.

 

Погрешности измерений.

погрешность результата измерения - это отклонение результата измерения (X_изм) от истинного (действительного) значения (X_{ист(действ)}) измеряемой величины.

ΔX=X_изм-X_{ист(действ)} абсолютной погрешности

относительной по­грешности

или в процентах

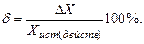
Точность измерений — качество измерения, отражающее близость их результатов к истинному значению изме­ряемой величины. Количественно точность измерения может быть выражена– 1/δ.

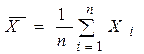,В качестве истинного значения при многократных измерениях одного и того же параметра используют среднее арифметическое значение :

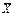где X_i – результат i-го единичного измерения; n – число единичных измерений в ряду.

Для оценки возможных отклонений X от X_ист определяют среднюю квадратичную погрешность

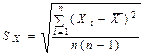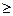,СКП , при n<20 , при n 20,

отсюда 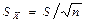, т.е. СКП из серии измерений всегда меньше, чем в каждом отдельном измерении, отсюда следует, что для повышения точности измерений необходимо увеличивать число измерений.

Инструментальная по­грешность — составляющая погрешности измерения, зависящая от погрешностей применяемых средств. По­грешность метода измерения — погрешности измере­ния, вызванная несовершенством метода измерений. Погрешность настройки — составляющая, возникающая из-за несовершенства осуществления процесса настройки. Погреш­ность отсчитывания — составляющая погрешности измерения, вы­званная недостаточно точным отсчитыванием показаний средств из­мерений. Погрешность по­верки — погрешность измерений при поверке средств измерений.

Систематиче­ская погрешность измерения — составляющая погрешности измере­ния, остающаяся постоянной или изменяющаяся по определенному закону при повторных измерениях одной и. той же величины.

, Суммарная предельная погрешность

где - алгебраическая сумма систематических погрешностей,

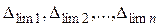- случайные предельные погрешности.

Температурная погрешность подсчитывается по формуле

∆ l = l [α₁ (t₁ – 20) – α₂ (t₂ – 20)], где ∆ l – погрешность измерения;

l - номинальный размер;

α₁ и α₂ – коэффициенты линейного расширения материалов измеряемого объекта и измерительного средства; t₁ и t₂ – температуры измеряемого объекта

Виды средств измерений.

Технические средства, используемые при измерениях и имеющие нормированные метрологические свойства, называют средствами измерения (СИ).

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: