Допуски и посадки гладких соединений деталей из пластмасс.

Особенности физико-механических свойств пластмасс, оказывающих влияние на величины зазора и натяга в соединении, привели к необходимости разработки специальных нормативных документов по допускам для деталей из пластмасс.

Допуски и посадки гладких соединений деталей из пластмасс регламентированы ГОСТ 25349-82 и охватывают диапазон размеров от 1 до 500 мм. Стандарт распространяется на гладкие сопрягаемые и несопрягаемые элементы и устанавливает поля допусков, причем основные положения и числовые значения допусков и основных отклонений, правила образования полей допусков и обозначений принимаются точно соответствующими ГОСТ 25346-82.

Ряды полей допусков для деталей из пластмасс являются ограничением рядов полей допусков по ГОСТ 25347-82 и, кроме того, включают дополнительные поля допусков, не вошедшие в этот стандарт, но образованные на основе ГОСТ 25346-82.

Дополнительные поля допусков, не предусмотренные ГОСТ 25347-82 и применяемые в отдельных технически обоснованных случаях, таковы: для валов ay11, az11, ze11; для отверстий AY11, AZ11, ZE11.

По ГОСТ 25349-82 установлены рекомендуемые посадки в соединениях пластмассовых деталей друг с другом. В соединениях деталей из пластмасс и металла за основную деталь целесообразно принимать металлическую с целью использования стандартных режущих инструментов при ее обработке. При выборе посадки в соединениях пластмассовых деталей с металлическими для последних рекомендуется назначать поля допусков по ГОСТ 25347-82: для валов – h7, h8, h9, h10, h11, h12; для отверстий – H7, H8, H9, H10, H11, H12.

Кроме посадок, указанных в ГОСТ 25349-82, возможно образование других посадок из полей допусков валов и отверстий. Например, в соединениях пластмассовых деталей друг с другом, требующих, как правило, бóльших зазоров или натягов, чем в соединениях с металлическими деталями, могут быть целесообразны посадки, образованные полями допусков отверстий, взятыми из системы вала, с полями допусков валов, взятыми из системы отверстия.

46. Классификация размерных цепей. Сущность расчета размерной цепи.
Основные термины, обозначения и определения размерных цепей Размерной цепью называют совокупность размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи. Например, с помощью размерных цепей можно определить точность взаимного расположения осей и поверхностей одной детали {подетальная размерная цепь) или нескольких деталей в сборочной единице или механизме {сборочная размерная цепь}. Замкнутость размерного контура — необходимое условие для составления и анализа размерной цепи. Однако на рабочем чертеже размеры следует проставлять в виде незамкнутой цепи; не проставляют размер замыкающего звена, так как для обработки он не требуется. Размеры, образующие размерную цепь, называют звеньями размерной цепи.

По взаимному расположению звеньев размерные цепи делятнаплоские и пространственные. Размерную цепь называют плоской, если ее звенья расположены в одной или нескольких параллельных плоскостях. Пространственной называют размерную цепь, звенья которой непараллельны одно другому и лежат в непараллельных плоскостях. Размерные цепи, звеньями которых являются линейные размеры, называют линейными. Размерные цепи, звеньями которых являются угловые размеры, называют угловыми. Размерная цепь состоит из составляющих звеньев и одного замыкающего. Замыкающим называют размер А_D,. Его значение и точность зависят от значений и точности остальных (составляющих) размеров цепи. Составляющее звено — звено размерной цепи, изменение которого вызывает изменение замыкающего звена (но не может и не должно вызывать изменение исходного звена). Исходное звено — звено размерной цепи, заданные номинальный размер и предельные отклонения которого определяют функционирование механизма и должны быть обеспечены в результате решения размерной цепи. Исходя из предельных значений этого размера рассчитывают допуски и отклонения всех остальных размеров цепи. В процессе сборки исходный размер, как правило, становится замыкающим. В подетальной размерной цепи размер, исходя из точности которого определяется степень точности остальных размеров, также называют исходным.

Расчет и анализ размерных цепей позволяет: установить количественную связь между размерами деталей машины и уточнить номинальные значения и допуски взаимосвязанных размеров исходя из эксплуатационных требований

Сущность расчета размерной цепи заключается в установлении допусков и предельных отклонений всехее звеньев исходя из требований конструкции и технологии. При этом различают две задачи: прямую и обратную.

Суть прямой задачи состоит в определении предельных отклонений составляющих размеров по заданным номинальным размерам всех размеров цепи и заданным предельным размерам исходного размера (при проектном расчете размерной цепи).

Суть обратной задачи состоит в определении номинального размера и предельных отклонений замыкающего звена по заданным номинальным размерам и предельным отклонениям составляющих звеньев (при проверочном расчете размерной цепи).

47. Чтобы обеспечить полную взаимозаменяемость, размерные цепи рассчитывают методом максимума-минимума, при котором допуск замыкающего размера определяют арифметическим сложением допусков составляющих размеров. Метод расчета на максимум-минимум, обеспечивает заданную точность сборки без подгонки (подбора) деталей.

В общем случае при n увеличивающих и p уменьшающих размерах номинальный размер замыкающего звена линейной размерной цепи можно определить по формуле:

A_D=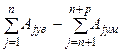

Это уравнение справедливо и в случае, когда вместо номинальных взяты значения соответствующих действительных размеров размерной цепи.

Прямая задача. Онаявляется наиболее важной, так как конечная цель расчета допусков составляющих размеров при заданной точности сборки— обеспечить выполнение машинойеефункционального назначения. Точность составляющих размеров должна быть такой, чтобы гарантировалась заданная точность ис­ходного (функционального) размера.

Способ равных допусков применяют, если составляющие размеры имеют один порядок (например, входят в один интервал диаметров) и могут быть выполнены с примерно одинаковой экономической точностью.

TA₁ = ТА₂ =...= Та_m-1 =T_срА_j.

Способ допусков одного квалитета применяют, если все составляющие цепь размеры могут быть выполнены с допуском одного квалитета и допуски составляющих размеров зависят от их номинального значения.

1. Выявление составляющих звеньев размерной цепи (увеличивающих и уменьшающих).

2. Составление графической схемы размерной цепи.

3. Определение среднего количества единиц допуска a_m по формуле

4. Назначение компенсирующего звена A_к из числа уменьшающих, а также допусков TA_j составляющих звеньев, кроме компенсирующего, по выбранному квалитету.

5. Выбор знаков предельных отклонений составляющих звеньев, кроме компенсирующего. Для охватывающих составляющих звеньев назначают предельные отклонения как для основного отверстия (EI=0), для охватываемых – как для основного вала (es=0) и для смешанных (ступенчатых) – симметричные предельные отклонения (± TA_j /2).

6. Расчет предельных отклонений компенсирующего звена по формулам:

7. Выбор стандартного поля допуска компенсирующего звена.

8. Проверка решения по уравнениям для наибольшего и наименьшего значений замыкающего звена - полученные значения предельных размеров замыкающего звена не должны выходить за заданные.