 |
Тема 5: Вариационный анализ
|
|
|
|
§1. Вариация признаков и ее причины
§2. Ряды распределения
§3. Структурные характеристики вариационного ряда.
§4. Показатели силы вариации.
§5. Показатели интенсивности вариации
§6. виды дисперсии. Правило сложения дисперсии.
§1.
Вариацией значения какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени.
Причина вариации: разные условия существования ЕСС именно вариация порождает необходимость в такой науке как статистика.
§2.
Проведение вариационного анализа начинается с построения вариационного ряда – упорядоченное распределение единиц совокупности по возрастающим или по убывающим признакам и подсчет соответствующих частот.
Ряды распределения
ü ранжированные
ü дискретные
ü интервальные
Ранжированный вариационный ряд – перечень отдельных ед. совокупности в порядке возрастания убывания ранжированного признака
| БАНК | Капитал тыс. руб. |
| СБ РФ | 96007237 |
| Внешторгбанк | 47991724 |
Дискретный вариационный ряд – таблица состоящая из 2х строк – полимерных значений варьирующего признака и кол-во единиц с данным значением признака.
| Кол-во детей в семье | 0 | 1 | 2 | 3 | 4 |
| Кол-во семей | 20 | 40 | 45 | 10 | 5 |
Интервальный вариационный ряд строится в случаях:
1. признак принимает дискретные значения, но кол-во их слишком велико
2. признака принимает любые значения в определенном диапазоне
| Размер собственного капитала тыс. руб. | 0 - 10000 | 10000-50000 | Свыше 50000 |
| Количество банков | 20 | 40 | 10 |
При построении интервального вариационного ряда необходимо выбрать оптимальное количество групп, самый распространенный способ по формуле Стерджесса
|
|
|
k=1+3.32lgn
k – количество интервалов
n – объем совокупности
При расчетах почти всегда получают дробные значения, округления производить до целого числа.
Длина интервала – l
Виды интервалов
1. нижняя граница последующего интервала повторяет верхнюю границу последующего интервала
| 0 - 10 | 10 - 20 | 20 - 30 |
2. С индивидуальными границами в интервал входят верхняя и нижняя границы
| 0 - 9 | 10 - 19 | 20 - 29 |
3. открытый интервал, интервал с одной границей
| До 5 | 5 - 10 | 10 – 15 |
В случае открытого интервала l принимается равной длине смежного с ним интервала, либо исходя из логических соображений.
| Стаж | До 5 | 5-7 | 7-9 |
| Кол-во рабочих |
При расчетах по интервальному вариационному ряду за xi принимается середина интервала.
 |
Интервалы могут быть как равные так и нет. При изучении вариационного ряда существенную помощь оказывает графическое изображение. Дискретный вариационный ряд изображается с помощью полигона.
Интервальный вариационный ряд изображается с помощью гистограммы.
 |
Накопленная частота
| x i | 0 | 1 | 2 | 3 | 4 |
| fi | 20 | 40 | 45 | 10 | 5 |
NME=60 медиана = 1
Кумулята – распределение меньше чем
 |
Огива – распределение больше чем
§3.
Медиана – значение признака делящее всю совокупность на две равные части.
Для дискретного вариационного ряда расчет медианы: если n-четное, то №Ме медианой единицы
Интервальный вариационный ряд:
k – количество интервалов
х0 – нижняя граница медианного интервала
l – длина медианного интервала
- сумма частот
- накопленная частота интервала предшествующая медианному.
- частота медианного интервала
Медианный интервал – первый интервал накопленная частота которого превышает половину от общей суммы частот.
| 0-5 | 5-10 |  10-15
| 15-20 |
| 15 | 20 | 40 | 25 |
|
|
|
Графически медиана находится по кумуляте.
2. Квартили – значение признака делящее совокупность на 4 равные части.
1ый квартиль 
3ий квартиль 
2ой квартиль – медиана.
xQ 1 xQ3 – нижняя граница интервала содержащего 1го и 3го квартили.
l – длина интервала
и 
- накопленные частоты интервалов предшествующих интервалов содержащих 1 и 3 квартили.
- частоты квартильных интервалов.
Для характеристики вариационного ряда используются:
Децили – делят совокупность на 10 равных частей, Перцитили – делят совокупность на 100 равных частей.
3. Мода – часто встречающаяся характеристика признака. Для дискретного вариационного ряда – наибольшая частота. Для интервального вариационного ряда мода рассчитывается по следующей формуле:
- нижняя граница модального интервала
l – длина модального интервала
fMo – частота модального интервала
fMo+1 – частота интервала следующего за модальным
Модальный интервал – интервал с наибольшей частотой. Графически мода находится по гистограмме.
§4.
1. Размах вариации 
2. Среднее линейное отклонение
- взвешенная
3. Дисперсия:
- взвешенная
4. Средне квадратическое отклонение
Свойство дисперсии.
1. 
1. уменьшение всех значений признака на одну и ту же величину не меняет величину дисперсии.
2. Уменьшение всех значений признаков в к раз уменьшает величину дисперсии в к2 раз, а СКО в к раз
3. 
если исчислить средний квадрат отклонений от любой величины А отличающийся от средней арифметической, то он всегда будет больше среднего квадрата отклонений исчисленного из средней арифметической. Таким образом 
от средней всегда меньше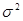 
исчисленной от любой другой величины т.е. она имеет свойство минимальности. СКО=1,25 
-при распределениях близких к нормальному.
В условиях нормального распределения существует следующая зависимость между 
и количеством наблюдений в пределах 
находится 68,3% наблюдений.
В пределах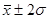 
находится 95,4% наблюдений
В пределах 
находится 99,7% наблюдений
§5.
Для сравнения вариации признаков в разных совокупностях или для сравнения вариации разных признаков в одной совокупности используются относительные показатели, базой служит средняя арифметическая.
|
|
|
1. Относительный размах вариации.
2. Относительное линейное отклонение
3. Коэффициент вариации
данные показатели дают не только сравнительную оценку но и образуют однородность совокупности. Совокупность считается однородной если коэффициент вариации не превышает 33%.
§6
На ряду с изучением вариации признака по всей совокупности в целом, часто бывает необходимо проследить количественные изменения признака, но группам, на которые делится совокупность и между ними. Эта достигается путем вычисления разных видов.
Виды дисперсии:
1. Общая дисперсия 
2. Межгрупповая дисперсия 
3. Внутригрупповая дисперсия (остаточная) 
1. измеряет вариацию признака во всей совокупности под влиянием все факторов обусловивших данную вариацию
Пример: потребление йогурта: при выборке 100 человек
Возраст
Доход
Социальное положение
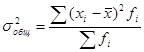
xi –индивидуальное значение признака
- среднее значение признака по всей совокупности
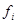- частота этого признака.
2. характеризует вариацию признака под влиянием признака фактора положенного в основу группировки.
- средняя по группе
- общая средняя по группе
- частота по группе
3. характеризует вариацию признака под влиянием факторов не включенных в группировку
x ij – i значение признака в j группе
- среднее значение признака в j группе
fij – частота i-го признака в j группе
Существует правило которое связывает 3 вида дисперсии, оно называется правило сложения дисперсии.
- остаточная дисперсия по j группе
- сумма частот по j группе
n – общая сумма частот
§7
основная задача анализа вариационных рядов – выявление закономерности распределения частот.
Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду в функционально связанным изменением значения признака.
 |
Кривую распределения можно построить с помощью полигона и гистограммы. Целесообразно свести эмпирическое распределение к теоретическому, к одному из хорошо изученных виду.
|
|
|
Кривая нормального распределения.
Различают следующие разновидности кривых распределения:
1. одновершинные
2. много вершинные
Для однородных совокупностей характерны одновершинные кривые, много вершинная кривая говорит о неоднородности совокупности и необходимости перегруппировки.
Выяснение общего характера распределения предполагает оценку его однородности, и расчет асимметрии и эксцесса. Для симметричных распределений 
Для сравнительного изучения асимметрии различных распределений вычисляется коэффициент асимметрии As.
где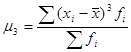 
- центральный момент третьего порядка; 
- СКО в кубе;
Если 
, то асимметрия значительная
Если As<0, то As – левосторонняя, если As>0, то As – правосторонняя.
Если 
, то As незначительная. Для симметричных и умеренно асимметричных рассчитывается показатель эксцесса: 
, если Ек>0, то распределение островершинное, если Ek<0, то распределение плосковершинное.
§8.
Вариация альтернативного признака количественно проявляется следующим образом.
0 – единицы не обладающие данным признаком;
1 – единицы обладающие данным признаком;
Пусть:
р – доля единиц обладающих данным признаком;
q – доля единиц не обладающих данным признаком;
тогда p+ q=1.
Альтернативный признак принимает 2 значения 0 и 1 с весами p и q.
; 
Прямые признаки – это такие признаки, величина которых увеличивается с увеличением исследуемого явления.
Обратные признаки – признаки, величина которых уменьшается с увеличением исследуемого явления.
 |
Максимальная дисперсия доли равна 0,25.
|
|
|
