 |
Тема 6: Моделирование рядов распределения.
|
|
|
|
§1. Фактическое и теоретическое распределение
§2. Кривая нормального распределения.
§3. Проверка гипотезы о нормальном распределении.
§4. Критерии согласия: Пирсона, Романовского, Колмогорова.
§5. Практическое значение моделирования рядов распределения.
Фактическое и теоретическое распределение
Одна из важнейших целей изучения рядов распределения состоит в том, чтобы выявить закономерность распределения и определить ее характер. Закономерности распределения наиболее отчетливо проявляются только при большом количестве наблюдений.
Фактическое распределение может быть изображено графически с помощью кривой распределения – графически изображается в виде непрерывной линии изменения частот в вариационном ряду функционально связанного с изменением варианта.
Под теоретической кривой распределения понимается кривая данного типа распределения в общем виде исключающего влияние случайных для закономерности факторов.
Теоретическое распределение может быть выражено аналитической формулой которая называется аналитической формулой. Наиболее распространенным является нормальное распространение.
Кривая нормального распределения.
Закон нормального распределения:
;
у – ордината нормального распределения
t – нормированное отклонение.
; е=2,7218; xi – варианты вариационного ряда; 
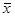- среднее;
Свойства:
Функция нормального распределения – четная, т.е. f(t)=f(-t), 
. Функция нормального распределения полностью определяется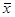 
и СКО.
Проверка гипотезы о нормальном распределении.
Причиной частого обращения к закону распределения является то, что зависимость возникающая в результате действия множества случайных причин ни одна из которых не является преобладающей. Если в вариационном ряду рассчитали Мо=Ме, то это может указывать на близость к нормальному распределению. Наиболее точная проверка соответствия нормальному закону производится с помощью специальных критериев.
|
|
|
Критерии согласия: Пирсона, Романовского, Колмогорова.
Критерий Пирсона.
- теоретическая частота
- эмпирическая частота
Методика расчета теоретических частот.
1. Определяется среднее арифметическое и 
по интервальному вариационному ряду, считается t по каждому интервалу.
2. Находим значение плотности вероятности для нормированного закона распределения. 
СТР.49
3. Находим теоретическую частоту. 
l – длина интервала
- сумма эмпирических частот
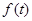- плотность вероятности
округлить значение до целых
4. Расчет коэффициента Пирсона
5. табличное значение 
d.f. – количество интервалов – 3
d.f. – количество степеней свободы.
6. если > 
, то распределение не является нормальным, т.е. гипотеза о нормальном распределении отменяется. Если 
< 
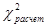, то распределение является нормальным.
Критерий Романовского.
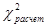- критерий Пирсона расчетный;
- число степеней.
Если С<3, то распределение близко к нормальному.
Критерий Колмогорова
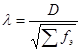, D – максимальное значение между накопленными эмпирическими и теоретическими частотами. Необходимое условие для использования Колмогорова: Число наблюдений более 100. По специальной таблице вероятностей 
с которой можно утверждать, что данное распределение является нормальным.
Практическое значение моделирования рядов распределения.
1. возможность применить к эмпирическому распределению законов нормального распределения.
2. возможность использования правила 3х сигм.
3. Возможность избежать дополнительных трудоемких и затратных расчетов, по исследованию совокупности зная, что распределение нормальное.
|
|
|
|
|
|
