 |
Ошибки выборочного наблюдения.
|
|
|
|
 |
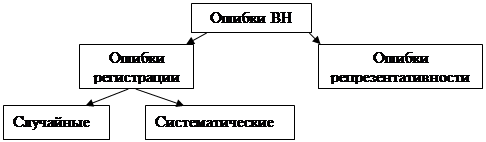Ошибки репрезентативности возникают только при выборочном наблюдении. Возникают в силу того, что выборочная совокупность не может в точности воспроизвести генеральную совокупность. Избежать их нельзя, но они легко поддаются прогнозированию и при необходимости их можно свести к минимуму.
Ошибка выборочного наблюдения – это разности между величиной параметра в генеральной совокупности и его величиной вычисленной по результатам выборочного наблюдения. Dх=-m+ 
, Dх – предельная ошибка в выборке, m - генеральная средняя; 
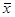- выборочная средняя.
Предельная ошибка выборки – величина случайная исследованию закономерностей случайны ошибок выборки посвящены работы Чебышева. В теореме Чебышева доказано, что Dх не превышает: 
- средняя ошибка выборки.t-коэффициент доверия указывает на вероятность данной ошибки. Стр 42-43.
В случае, когда нужно определить t по известной F(t) берем F(t) ближайшую большую и по ней определяем t.
Предельная ошибка доль
, р – доля.
Если отбор был осуществлен бесповторным способом, то в формулы предельных ошибок добавляется
- поправка на бес повторность.
Для каждого вида выборочного наблюдения представленная ошибка, рассчитываются по разному:
1. собственно случайное и механическое наблюдение 
; 
2. Районированное наблюдение
3. Серийная выборка
r – количество серий в выборке;
R – количество серий в генеральной совокупности;
;
- меж групповая дисперсия доли.
Задачи выборочного наблюдения
Применяется для следующих задач:
1. n -? для определения объема выборки по известной F(t), Dx.
2. определение Dx выборки по известной F(t), n
3. определение F(t) по известным Dx и n
|
|
|
1 задача n -? Сначала n определяется по формуле повторного отбора 
, 
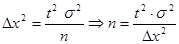для бесповторного отбора: 
Способы для определения дисперсии:
1. ее берут из предыдущих аналогичных исследований.
2. СКО» 
3. СКО при нормальном распределении» 1/6 размаха вариации.
4. если распределение заведомо асимметричное, то СКО» 1/5 размаха вариации
5. Для доли применяется дисперсия максимально возможная р(1-р)=0,25
6. при n³100, то s2=S2 – выборочная дисперсия
30£ n £100, то s2=S2(n/n-1), s2 – генеральная дисперсия
n<30, то S2 (малая, т.к. дисперсия выборочная) и все расчеты ведутся по S2
При расчете n не следует гнаться за большим значением t и за малыми предельными ошибками, т.к. это ведет к увеличению n следовательно, к увеличению затрат. По следующему закону аналогично.
Распространение данных выборочного наблюдения на генеральную совокупность.
Конечной целью любого ВН является характеристика генеральной совокупности.
Величины, рассчитанные по результатам ВН распространяются на генеральную совокупность с учетом предела их предельной ошибки.
Предположим, что потребление йогурта в месяц одним человеком.
250-20£m£250+20; 230£m£270
А всего 1000 человек
230000£m£270000
Для доли
p-Dp£p£p+Dp
48%-5%£p£48%+5%
43%£p£53%
Малая выборка.
В практике статистического исследования в современных условиях все чаще приходится сталкиваться с небольшими по объему выборками.
Малая выборка – выборка наблюдения численность единиц которого не превышает 30, n£30/
Разработка теории малой выборки была проделана английским статистом Госсет, писавшим под псевдонимом student в 1908 году.
Он доказал, что оценка расхождения между средствами малой выборки и генеральной выборки имеет особый закон распределения. При расчетах по малой выборке величина s2 не рассчитывается. tст для возможных пределов ошибки пользуются критерием student. Стр.44-45. 
- вероятность обратного события.
|
|
|
Количество степеней свободы
d.f=n-1,
предельная ошибка малой выборки
предельная ошибка доли
|
|
|
