§ 1. 4. Классификация антенно-фидерных устройств

§ 1. 4. КЛАССИФИКАЦИЯ АНТЕННО-ФИДЕРНЫХ УСТРОЙСТВ

Антенны классифицируют по диапазонам волн:

1) антенны длинных волн, т. е. антенны, работающие в диапазоне длин волн λ, больших 3000 м (λ > 5000 м);

2) антенны средних волн (λ = 100 - 3000 м);

3) антенны коротких волн (КВ) (λ = 10 - 100 м);

4) антенны сверхвысоких частот (СВЧ), которые в свою очередь подразделяются на:

а) антенны метровых волн (λ = 1 - 10 м);

б) антенны дециметровых волн (λ = 10 см - 1 м);

в) антенны сантиметровых волн (λ = 1 - 10 см);

г) антенны миллиметровых волн (λ = 1 - 10 мм);

д) антенны субмиллиметровых волн (λ = 1 - 0, 1 мм) и антенны оптического диапазона (λ < 0, 1 мм).

Такая классификация вызвана особенностью распространения радиоволн в различных диапазонах и различными возможностями в реализации требуемых характеристик, размеров антенн и точности их изготовления.

В конструктивном и электрическом отношениях антенны разных диапазонов имеют существенные различия.

В теории антенн при рассмотрении их основных характеристик и методов расчета независимо от диапазона работы принято выделять классы антенн:

остронаправленные;

диапазонные и сверхширокополосные;

электрически сканирующие;

слабонаправленные, устанавливаемые на борту ЛА, в которых учитывается явление дифракции на наружной поверхности ЛА.

В общей теории антенных устройств обычно деление на передающим и приемные антенны не проводится, хотя в конструктивном отношении их приходится различать. Каждый класс антенн может в свою очередь делиться на различные виды (типы), группы, причем в основу такого деления кладутся направленность действия, частотные свойства и другие основные характеристики.

Фидерные устройства или линии передачи, т. е. устройства, ко­торые канализируют электромагнитную энергию ВЧ или СВЧ, принято классифицировать по типу используемых волн: линии передач с вол­ной ТЕМ (рис. 1. 3 и 1, 4); волноводы (рис. 1, 5); линии передачи с поверхностными замедленными волнами (рис. 1. 6); лучевые волноводы и световоды (светопроводы) (рис. 1. 7).

С конструктивной точки зрения линии передачи подразделяются на жесткие и гибкие.

 

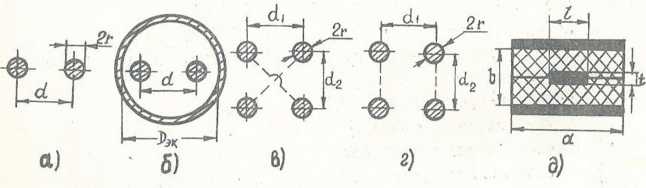
Рис. 1. 3. Симметричные линии:
а- открытая двухпроводная линия; б- экранированная двух­проводная линия;
в, г -четырехпроводные линии; д- симмет­ричная полосковая линия

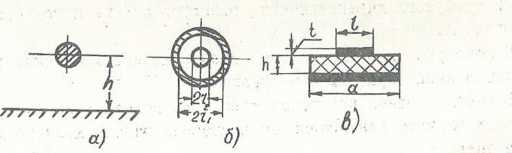
Рис. 1. 4. Несимметричные линии:
а - одиночный провод над экраном; б- коаксиальная линия;
в - несимметричная полосковая линия

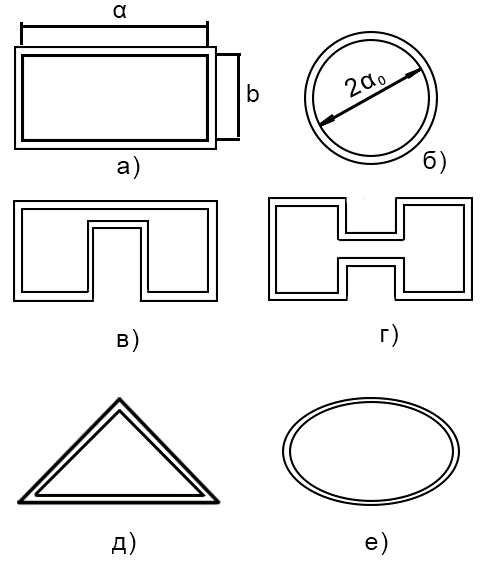
Рис. 1. 5. Различные виды волноводов:
а- прямоугольный металлический; б- круглый;
в- П-образный; г- Н-образный; д-треугольный; е- эллиптический;

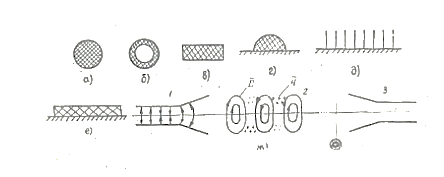
Рис. 1. 6. Линии с замедленными поверхностными волнами: а, б, в - круглый, трубчатый и прямоугольный диэлектрические волноводы; г- отражательная линия с полукруглым диэлектричес­ким стержнем; д- замедляющая металлическая структура типа " гребенки"; е - металлический лист, покрытый слоем диэлектри­ка; ж- провод, покрытый диэлектриком (однопроводная линия поверхностных волн): 1 - возбуждающее устройство; 2 - провод с замедляющей структурой; 3- приемное устройство

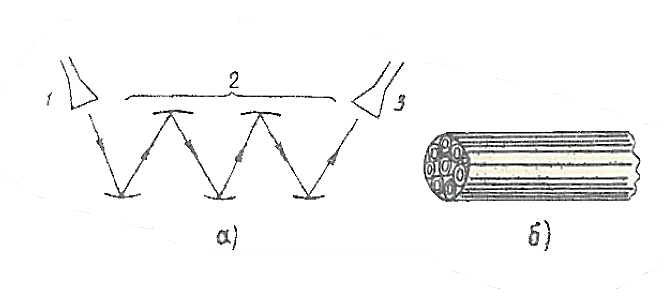
Рис, 1. 7. Линии передачи:
а- лучевой волновод; б- световод (стеклянные нити с отражающим покрытием);
1 - возбуждающее устройство; 2 - волновод; 3 - приемное устройство

Глава 2. ТЕОРИЯ ОДНОРОДНЫХ ЛИНИЙ ПЕРЕДАЧИ С ВОЛНОЙ ТЕМ

§ 2. 1. ТЕЛЕГРАФНЫЕ УРАВНЕНИЯ

Рассмотрение теории курса начнем с вопросов распространения электромагнитной энергии вдоль проводников, т. е. с теории длинных линий. Под длинными линиями будем понимать линии передачи энергии СВЧ, в которых распространяется волна типа ТЕМ. Эти линии переда­чи (фидерные устройства) в общем случае можно представить в виде некоторой линии передачи длиной l ≥ λ (рис. 2. 1), где λ -длина волы генератора. Под этой эквивалентной линией можно понимать двух - и четырехпроводные лилии, коаксиальные и полосковые линии, поперечные размеры которых выбраны таким образом, что в них обес­печивается условие существования только волны типа ТЕМ.

Расчет длинных линий может быть выполнен как строгим методом с использованием уравнений Максвелла, так и приближенно с помощью так называемого метода телеграфных уравнений. Второй метод приме­няется чаще, так как позволяет проще получить тот же результат.

В телеграфные уравнения входят в явном виде не поля, а их интегральные характеристики - напряжение и ток, а также интеграль­ные параметра линии - погонные емкость, индуктивность и волновое сопротивление. Эти уравнения получаются применением законов Кирхгофа к элементарным участкам данной линии, которые на эквивалентной схеме могут быть представлены в виде четырехполюсника с определенными сосредоточенными эквивалентными параметрами.

Рис. 2. 1. Длинная линия: а – выбор начала отсчета; б – эквивалентная схема элементарного участка длинной линии

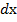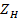Выделим элементарный участок  линии, находящейся на рас­стоянии  от нагрузки  (рис. 2. 1, а). Отсчет расстояния  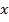бу­дем вести от конца линии, т. е. от нагрузки, в сторону генератора.

Выделенный элемент 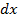 (рис. 2. 1, б) обладает бесконечно ма­лыми индуктивностью 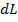, емкостью 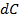, сопротивлением  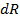и проводимостью утечки 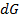, которые равны:  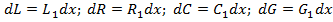- соответственно погонные индуктивность, емкость, сопротивление и проводи­мость утечки. Эти погонные параметры не зависят от длины линии l, так как рассматриваемая линия – однородная.

Решение будем проводить в предположении изменения напряжения и тока во времени по гармоническому закону, используя комплексную форму записи
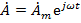, где 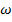 - угловая частота напряже­ния, приложенного к линии.

На выделенном элементарном участке линии dx вследствие па­раллельной проводимости 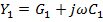 ток уменьшается, а последовательное сопротивление  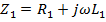приводит к уменьшению напряжения, что может быть выражено телеграфными уравнениями

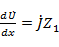                                                    ;                                             (2. 1)

Уравнения (2. 1) выражают связь между током и напряжением в любом сечении линии.

 

Решение телеграфных уравнений для общего случая наличия в линии как падающей, так и отраженной волн приводит к следующим выражениям, определяющим значения комплексных амплитуд напряжения 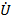 и тока  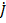в любом сечении линии через значения комплексных амплитуд напряжения и тока 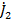 в конце ее:

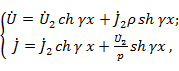                                                                                   (2. 2)

Где 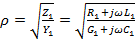 – волновое сопротивление линии;

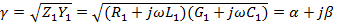- постоянная распространения;

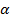 - постоянная затухания;

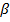- фазовая постоянная или волновое число.

Скорость распространения волн напряжения (тока) вдоль линии, или фазовая скорость, при наличии потерь в линии оказывается зависящей от частоты колебаний:

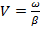. Коэффициент отражения в линии 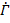, под которым понимается отношение комплексной амплитуды напряжения отраженной волны к комплексной амплитуде падающей волны в данном сечении линии, может быть определен по формуле

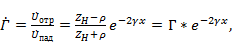                                                                      (2. 3)

где сопротивление нагрузки.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: