 |
Чисто активная нагрузка линии
|
|
|
|
В этом случае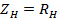 
, 
, 
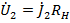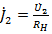и уравнения (2. 4) для напряжения и тока в линии можно записать в виде
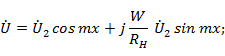
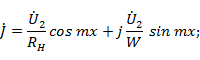
Введем обозначение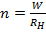 
. При этом 
.
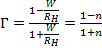Тогда
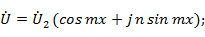
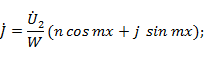
Отсюда действующие значения напряжения и тока
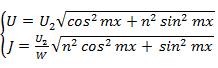(2. 5)
Возможны следующие три случая соотношения между сопротивлением нагрузки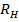 
и волновым сопротивлением линии 
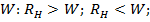и 
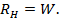
Случай 1: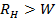 
, тогда 
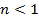. Напряжение достигает максимального значения 
в сечениях линии, соответствующих значениям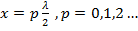 
На конце линии при этом - максимум напряжения и минимум тока (рис. 2. 5, а). Минимальное напряжение на линии будет в сечениях, определяемых соотношением 
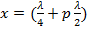, а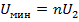 
.
Отношение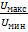 
называется коэффициентом бегущей волны в линии (КБВ). Обратная величина 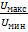называется коэффициентом стоячей волны (КСВ). В данном случае 
, 
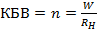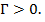В пределе при 
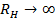приходим к линии, работающей в режиме холостого хода.
Случай 2: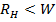 
, тогда 
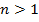. Из уравнений (2. 5) получаем (рис. 2. 5, б):
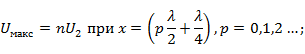
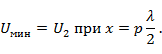
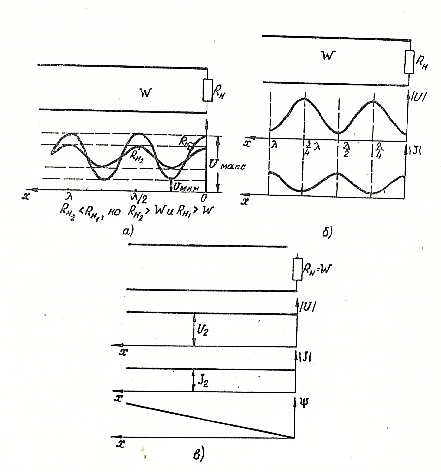
Рис. 2. 5. Линия, нагруженная на активное сопротивление:
а - 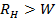; б - 
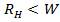; в -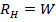 
Коэффициент бегущей волны в линии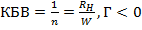 
. В пределе при 
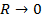приходим к короткозамкнутой линии.
Режим работы линии при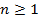 
называется режимом смешанных волн. В этом режиме амплитуда отраженной волны меньше амплитуды падающей волны: часть энергии потребляется в нагрузке.
Случай 3: 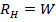, тогда 
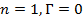. Для комплексных амплитуд напряжения и тока в линии в этом случае получаем
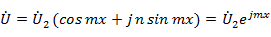
Таким образом:
1) в любом сечении линии напряжение и ток имеют одинаковые фазы и постоянную амплитуду (фазы напряжения и тока меняются вдоль линии по линейному закону) (рис. 2. 5, в);
2) отношение напряжения к току в любом сечении есть волновое сопротивление линии; линия имеет входное сопротивление равное волновому;
|
|
|
3) в линии имеет место только одна падающая волна, т. е. устанавливается режим бегущих волн.
Такой режим работы наиболее желателен на практике. Действительно, в режиме бегущих волн потери в линии минимальны, так как отсутствуют дополнительные омические потери, связанные с наличием отраженной волны. Кроме того, равномерное распределение напряжения вдоль линии (без максимумов и минимумов) позволяет передавать заданную мощность с минимальным напряжением. И, наконец, входное сопротивление линии в режиме бегущих волн не зависит от частоты и изменения длины линии.
Итак, в режиме бегущих волн 
и линия полностью согласована с нагрузкой.
Теоретически можно получить полное согласование, т. е. КБВ=1. Практически максимальное значение КБВ равно 0, 90 - 0, 95.
Входное сопротивление линии при чисто активной нагрузке
Учитывая выражения для напряжения и тока в линии
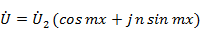
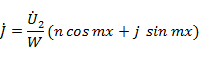
для входного сопротивления получаем
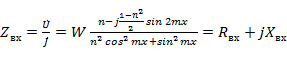(2. 6)
Следовательно, входное сопротивление в произвольном сечении линии при чисто активной нагрузке - комплексное. Оно активно только в сечениях линии, где имеют место максимумы и минимумы напряжения.
Допустим, что в формуле (2. 6):
1) 
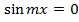, тогда 
;
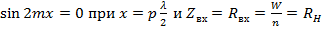2) 
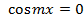, тогда 
.
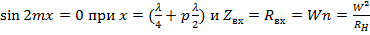Отсюда следует, что линия с отрезками длиной 
и 
является трансформатором сопротивлений: полуволновая линия трансформирует сопротивление без изменения, а четвертьволновая - как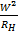 
.
Характер распределения активной и реактивной составляющих входного сопротивления вдоль линии в соответствии с выражением (2. 6) показан на рис. 2. 6 для двух значений сопротивлений нагрузки, причем .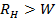
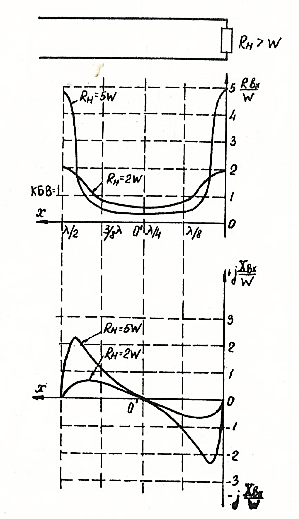
Рис. 2. 6. Зависимость сопротивления линии от ее длины при произвольной активной нагрузке
Как видно из графиков, реактивная составляющая входного сопротивления всюду конечна и ее максимальная величина тем меньше, чем ближе КБВ к единице. График реактивной составляющее вблизи сечений линии 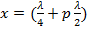похож на график входного сопротивления линии в режиме холостого хода. Поэтому составляющую 
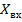в окрестности указанных сечений можно приближенно определить по формуле 
.
|
|
|
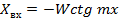Активная составляющая при своем изменении вдоль линии обязательно проходит через значения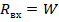 
. Однако в этих сечениях всегда присутствует реактивная составляющая сопротивления.
Если 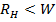, то графики изменения сопротивления сохраняют тот же характер, что и на рис. 2. 6, только начало координат должно быть смещено на четверть волны вправо или влево от точки 0, т. е. в то сечение, где имеет место минимум активной составляющей сопротивления. Если начало координат сместить в точку 
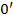, то графики рис. 2. 6 будут соответствовать значениям 
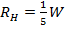и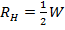 
.
|
|
|
