 |
Комплексная нагрузка линии. § 2.3. ЛИНИЯ С ПОТЕРЯМИ
|
|
|
|
Комплексная нагрузка линии
В этом случае, как и в случае активной нагрузки, происходит расход энергии на активной части нагрузки, и в линии устанавливается режим смешанных волн. Отличие от случая активной нагрузки состоит лишь в том фазовом сдвиге, который приобретает отраженная волна в месте включения нагрузки, т. е. в выбранном начале отсчета расстояния в линии. Тот или иной сдвиг фаз вызывает соответствующий сдвиг кривых тока и напряжения вдоль линии без изменения их формы (рис. 2. 7).
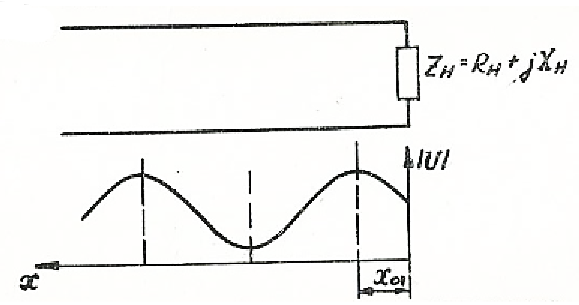
Рис. 2. 7. Распределение амплитуд напряжения
вдоль линии при комплексной нагрузке
Коэффициент отражения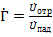 
в этом случае – комплексный.
Нетрудно установить связь между КБВ в линии и модулем коэффициента отражения Г:
Откуда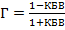 
.
При комплексной нагрузке КБВ в линии и расстояние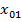 
от нагрузки до ближайшего максимума напряжения (рис. 2. 7) могут быть определены по формулам Татаринова
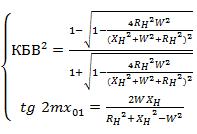(2. 7)
В сечении 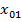входное сопротивление линии - чисто активное: 
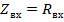. Согласно последней формуле при емкостной нагрузке 
, а при индуктивной 
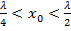, где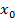 
– расстояние от ближайшего минимума напряжения до нагрузки.
Зная КБВ и расстояние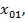 
при расчетах можно воспользоваться всеми формулами, выведенными ранее для линии с чисто активной нагрузкой, при условии подстановки в соответствующие соотношения вместо координаты 
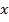значения 
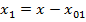, что соответствует переносу координат в точку экстремума (максимума) напряжения.
Входное сопротивление линии с комплексной нагрузкой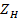 
равно
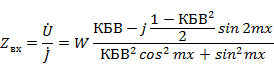
где КБВ определяется формулой (2. 7),
Как и в случае линии с чисто активной нагрузкой, нетрудно показать, что и в данном случае величина входного сопротивления периодически повторяется с периодом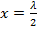 
:
|
|
|
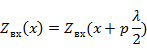
В линии при комплексной нагрузке имеют место сечения, где входное сопротивление чисто активное. Эти сечения находятся в экстремумах напряжения (тока) линии. Произведение входных сопротивлений для двух таких сечений, отстоящих друг от друга на 
, равно квадрату волнового сопротивления линии:
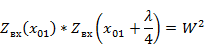
§ 2. 3. ЛИНИЯ С ПОТЕРЯМИ
В линии с потерями погонные параметры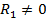 
и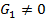 
. Поэтому постоянная распространения 
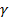- величина комплексная:
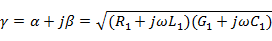
Возводя в квадрат обе части этого соотношения, приравнивая затем действительные и мнимые части и преобразовывая получающиеся уравнения, приходим к следующим формулам для постоянной затухания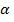 
и фазовой постоянной 
:
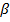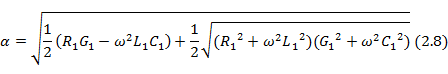
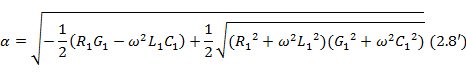
Учитывая, что в области радиочастот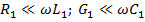 
, и отбрасывая малые величины высших порядков, можно выражения (2. 8) и (2. 8') привести к виду
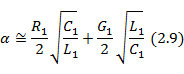
В случае малых потерь в линии можно считать, что
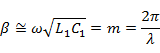
и фазовая скорость волны приблизительно равна скорости света: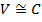 
.
Подставляя в (2. 9)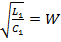 
, получаем для погонного затухания удобную расчетную формулу
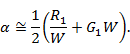
Так как в высокочастотных линиях, особенно без диэлектрического заполнения, утечкой 
можно пренебречь ( 
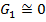), то
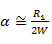
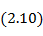
Погонное сопротивление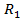 
, входящее в формулу (2. 10), определяется с учетом поверхностного эффекта и в случае круглого медного провода радиуса 
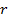равно
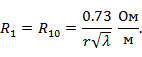
Для двухпроводной линии 
, для четырехпроводной линии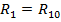 
, а для коаксиальной линии
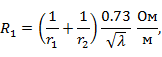
где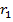 
и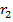 
- соответственно радиусы внешнего и внутреннего проводника коаксиальной линии, мм; 
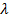- длина волны, м.
Сопротивление проводника с учетом шероховатости поверхности увеличивается и при высоте неровностей порядка глубины проникновения тока возрастает примерно в 1, 5 раза.
В тех случаях, когда линия с волной ТЕМ заполнена диэлектриком и проводимостью утечки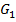 
пренебречь нельзя, ее можно подсчитать по формуле
|
|
|
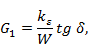
Зная постоянную распространения 
и волновое сопротивление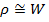 
, распределение напряжения и тока в линии можно определить по формулам (2. 2):
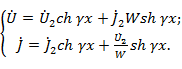(2. 11)
|
|
|
