 |
Теория идеальной линии. § 2. 2. Режимы работы линий. Свойства входных сопротивлений линий
|
|
|
|
Теория идеальной линии
Линия передачи, в которой отсутствуют активные потери мощности, называется идеальной линией. Реально такие линии не существуют. Однако при высоких частотах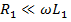 
и 
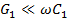. Поэтому потери мощности в проводах и окружающем пространстве оказываются настолько малыми, что ими можно пренебречь и считать, что 
, 
.
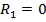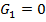В этом случае волновое сопротивление линии становится чисто активным и не зависящим от частоты:
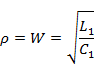
Так как постоянная затухания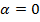 
, то постоянная распространения становится мнимым числом
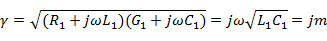
где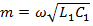 
- фазовая постоянная идеальной линии.
Фазовая скорость принимает значение
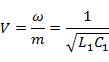
и оказывается независящей от частоты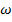 
.
Учитывая известное соотношение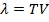 
и выражение для фазовой скорости, фазовую постоянную линии можно связать с длиной волны:
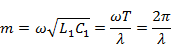
Как мы показали, фазовая скорость волны зависит от погонных параметров линии. Для определения последних необходимо использовать уравнения электродинамики и методы теории электромагнитного поля. Как следует из этой теории, во всех линиях, состоящих из проводов, существует волна типа ТЕМ, для которой справедливо равенство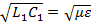 
, т. е. фазовая скорость
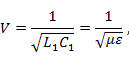
где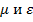 
- магнитная и диэлектрическая проницаемости окружающей среды.
Таким образом, скорость волны вдоль любых длинных линий без потерь равна скорости света в среде, окружающей проводник. Поэтому в воздушных линиях скорость волны равна скорости света, а длина волы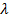 
- длине волны в вакууме 
:
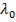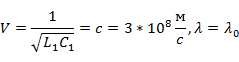
Наличие диэлектрика, окружающего провода линии, с параметрами, отличающимися от параметров воздуха, уменьшает скорость и длину волны:
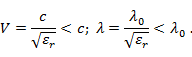
Заменяя в уравнениях (2. 2)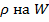 
и подставляя 
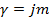, получаем выражения для комплексных амплитуд напряжения и тока идеальной линии в тригонометрической форме:
|
|
|
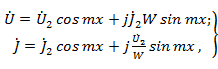(2. 4)
Пользуясь уравнениями (2. 4), можно определить значения комплексных амплитуд в любом сечении линии, если известны комплексные амплитуды напряжения и тока на конце её.
Для определения волнового сопротивления W длинной линии, входящего в уравнения (2. 4), достаточно знать погонные параметры лини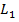и 
и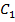 
.
Применение методов статики для определения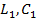 
и волнового сопротивления на высоких частотах дает следующие результаты:
I. Двухпроводная симметричная линия (рис. 1. 3, а):
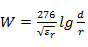Ом,
где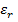 
- относительная диэлектрическая проницаемость окружающей среды.
Практические значения волнового сопротивления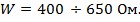 
2. Четырехпроводная линия с различными способами возбуждения: а) потенциал одинакового знака имеют накрест лежащие провода (рис. 1. 3, в):
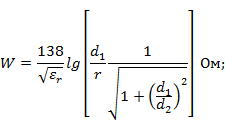
б) потенциал одинакового знака имеют провода, лежащие по одну сторону вертикальной плоскости симметрии (рис. 1. 3, г):
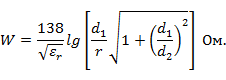
Волновое сопротивление таких линий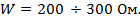 
3. Провод над экраном (землей) (рис. 1. 4, а):
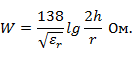
4. Коаксиальная линия (рис. 1. 4, б):
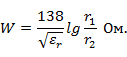
Используемые на практике коаксиальные линии имеют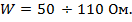 
5. Несимметричная полосковая линия, заполненная диэлектриком [II] (рис. 1. 4, в):
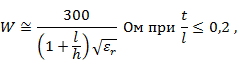
где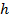 
- толщина листа диэлектрика;
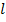– ширина полоски;
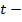толщина полоски.
Пределы изменения волнового сопротивления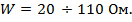 
6. Симметричная полосковая линия, заполненная диэлектриком [II] (рис. 1. 3, д):
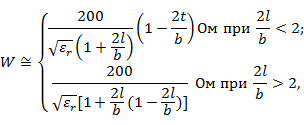
где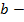 
расстояние между верхней и нижней заземленной пластинами.
Волновое сопротивление такой линии может быть легко реализовано в пределах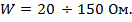 
§ 2. 2. РЕЖИМЫ РАБОТЫ ЛИНИЙ. СВОЙСТВА ВХОДНЫХ СОПРОТИВЛЕНИЙ ЛИНИЙ
Выше были приведены уравнения, описывающие в общем виде распределение напряжения и тока в линии при произвольной нагрузке на её конце.
|
|
|
Рассмотрим распределение напряжения, тока и сопротивления в идеальной линии для некоторых частных случаев.
|
|
|
