 |
Согласование с помощью четвертьволнового трансформаторе.
|
|
|
|
Согласование с помощью четвертьволнового трансформаторе.
Данный способ основан на следующем свойстве входных сопротивлений линии:
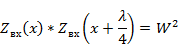
Трансформатор представляет собой отрезок линии длиной 
с волновым сопротивлением 
, не равным волновому сопротивлению фидера 
. Он включается между линией и активной нагрузкой (рис. 3. 1, а). Для того чтобы вдоль линии на участке от генератора до трансформатора был режим бегущей волны, необходимо выполнение условия 
. Тогда
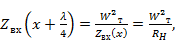или 
, откуда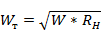 
.
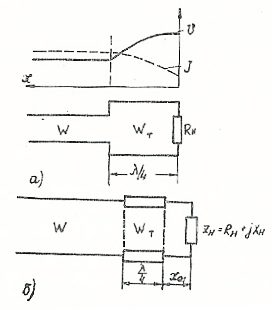
Рис. 3. 1. Согласующий четвертьволновый трансформатор:
а - активная нагрузка линии; б - комплексная нагрузка линии
Если трансформатор нельзя непосредственно включить у нагрузки по конструктивным соображениям, то его можно включить в тех сечениях линии, где входное сопротивление ее чисто активное (в экстремумах напряжения или тока), с учетом соответствующего входного сопротивления в этих сечениях.
Четвертьволновый трансформатор можно использовать и для согласования комплексной нагрузки. С этой целью его включают в сечении максимума напряжения в линии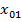 
, где входное сопротивление чисто активное (рис. 3. 1, б). Это сечение определяется формулой
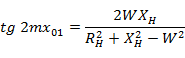
Трансформатор можно включить и в сечение 
, где имеется минимум напряжения.
В сечении 
входное сопротивление 
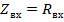и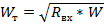 
. Если в этом сечении - максимум напряжения, то 
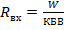; Если минимум напряжения, то 
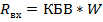. В первом случае необходим триноформатор с повышенным волновым сопротивлением 
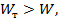а во втором - с пониженным 
.
Четвертьволновые трансформаторы используются как в симметричных двухпроводных линиях, так и в коаксиальных и полосковых линиях.
Для изменения волнового сопротивления линии необходимо изменить или диаметр проводов, или расстояние между ними, или параметры окружающей среды. Примеры выполнения трансформатора сопротивления в коаксиальной и полосковой линиях показаны на рис. 3. 2.
|
|
|
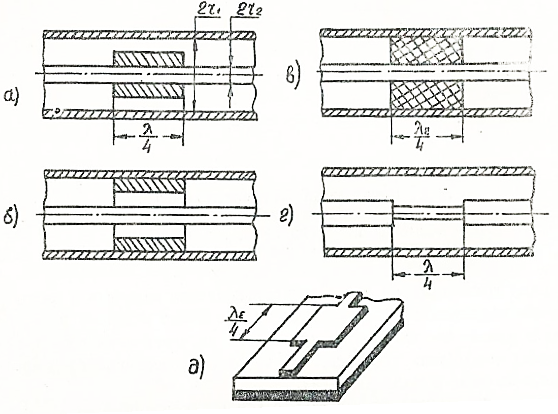
Рис. 3. 2. Четвертьволновые трансформаторы в коаксиальной и полосковой линиях, выполненные в виде:
а, б – металлических втулок; в – диэлектрической втулки;
г – проточки в центральном проводнике линии; д – рабочей полоски измененной ширины
Согласование с помощью передвижного параллельного шлейфа
Метод пригоден при любой нагрузке - активной или комплексной. В диапазоне КВ и УКВ параллельный шлейф представляет собой отрезок: фидера, замкнутый на конце. Длина его обычно меньше . Шлейф подключается параллельно фидеру вблизи нагрузки (рис. 3. 3).
Рис. 3. 3. Передвижной параллельный шлейф
Положение и длина шлейфа зависят от степени рассогласования нагрузки и фидера. Теория такого способа согласования разработана В. В. Татариновым в 1929 г.
Для получения согласования шлейф, имеющий входное сопротивление индуктивного характера, необходимо включить в такое сечение линии, где входное сопротивление комплексное и такое, что реактивная составляющая имеет емкостной характер, а активная равна w фидера. Подбором величины индуктивности шлейфа добиваются резонанса так, чтобы входное сопротивлении линии в сечении аб (рис. 3. 3. ) было бы равно w.
Таким образом, условие получения режима бегущей волны в линии в случае параллельного шлейфа, включенного в сечение аб, следующее:
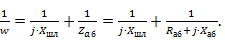
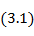
Составляющие входного сопротивления 
и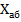 
, входящие в формулу (3. 1), можно определить по формулам теории линий, если отсчет расстояния x1 вести от ближайшего к нагрузке максимума напряжения до точки включения шлейфа:
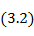
Подставляя (3. 2) в формулу (3. 1) и приравнивая между собой действительные и мнимые части уравнения, получаем расчетные соотношения
|
|
|
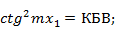
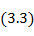
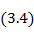
Где Хшл - реактивное входное сопротивление шлейфа;
КБВ - коэффициент бегущей волны в линии при произвольной нагрузке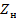 
на ее конце.
Так как параллельный шлейф представляет собой короткозамкнутый отрезок линии, то
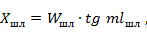
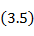
где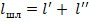 
- длина шлейфа.
Приравнивая выражения (3. 4) и (3. 5), получаем формулу определения длины шлейфа
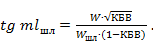
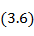
По формулам (3. 3) и (3. 6) можно непосредственно определить место включения шлейфа и его длину для получения в линии режима бегущей волны при произвольной комплексной нагрузке. Исходные данные о величине КБВ и о положении максимума напряжения 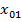относительно нагрузки обычно определяются экспериментальным путем.
|
|
|
