Согласование с помощью двух и трех неподвижных шлейфов

Согласование с помощью двух и трех неподвижных шлейфов

В связи с трудностью осуществления подвижных шлейфов в экранированных линиях (коаксиальных, волноводных и др. ) в качестве согласующего устройства этих линий применяются двух - и трехшлейфовые согласующие схемы. В таких устройствах положение шлейфов вдоль линии фиксировано; их волновые сопротивления определяются из конструктивных соображений, а необходимыми степенями свободы при настройке являются длины шлейфов. На рис. 3. 4, а показана схема согласования с двумя неподвижными шлейфами. 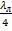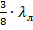Расстояние между шлейфами l обычно выбирается равным  или  , где 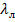 - длина волны в линии.

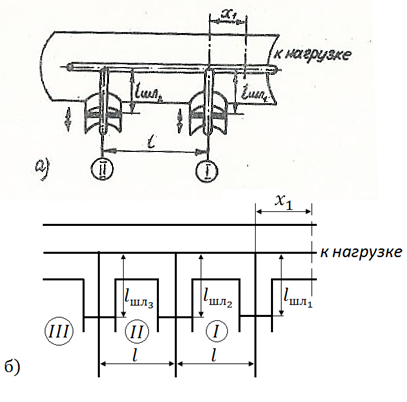
Рис. 3. 4. Согласующее устройство:

а - в виде двух шлейфов; б - в виде трех шлейфов

Меняя длину первого шлейфа 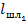 , изменяем входную комплексную проводимость в сечении второго шлейфа до тех пор, пока ее активная часть не станет равной волновой проводимости линии. Реактивная составляющая входной проводимости в этом сечении компенсируется выбором соответствующей длины второго шлейфа  .

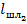Согласование с помощью двух шлейфов возможно не при всех значениях нагрузки. Оно возможно, если при данной нагрузке расстояние 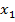 (рис. 3. 4) удовлетворяет неравенству

                                                                                                    

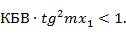
Поэтому при произвольной нагрузке вместо двухшлейфового согласующего устройства используют трехшлейфовое (рис. 3. 4, б). Если расстояние 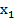 от первого шлейфа до ближайшего к нагрузке максимума напряжения удовлетворяет вышеприведенному неравенству (3. 7), согласование осуществляется первым и вторым шлейфами. Если же  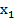удовлетворяет условию  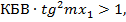то согласования добиваются вторым и третьим шлейфами. Свободный шлейф исключают из работы путем выбора его длины, равной  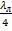. Следует отметить, что возможен такой порядок согласования, когда используется регулировка всех трех шлейфов.

Кроме рассмотренных способов с параллельными шлейфами, на практике находят применение и последовательные шлейфы, включаемые в разрыв линии. Эти шлейфы могут быть как короткозамкнутыми, так и разомкнутыми. Условие согласования: входное сопротивление в месте разрыва линии - активное и равно волновому сопротивлению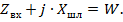

Параметры согласующего устройства (рис. 3. 5, а) могут быть при этом определены из соотношений

Последовательные короткозамкнутые шлейфы находят также применение в дроссельных секциях подвижных соединений коаксиальных линий (рис. 3. 5, б).

Рис. 3. 5. Согласование с помощью последовательно

включенного в линию шлейфа:

а - место включения шлейфа; б, в - конструктивная

и эквивалентная схемы последовательного шлейфа в

подвижном соединении коаксиальной линии;

1 - трущиеся контакты; 2 - точка контакта.

Как видно из рисунка, в сечениях А и Б последовательно с внутренним и внешним проводниками линии включены замкнутые на конце полуволновые линии, осуществляющие бесконтактное короткое замыкание по высокой частоте двух вращающихся относительно друг друга частей линии I и II. Таким образом, можно считать, что нарушения однородности линии не происходит и в ней устанавливается режим, близкий к бегущей волне.

§ 3. 3. ОСНОВНЫЕ ПРИНЦИПЫ ШИРОКОПОЛОСНОГО СОГЛАСОВАНИЯ

Характерной особенностью рассмотренных методов узкополосного согласования является то, что они рассчитаны на получение полного согласования в линии (КБВ = I) только на одной определенной частоте рабочего диапазона частот. Степень рассогласования на других частотах зависит как от частотных свойств нагрузки, так и от согласующих элементов и в общем случае может быть любой.

В случае необходимости обеспечить согласование в диапазоне частот порядка десяти процентов и более, а также при использовании сигналов с широкополосным спектром применяются методы широкополосного согласования. Эти методы характерны тем, что полное согласование не достигается на всех частотах диапазона, однако рассогласование в заданной полосе не превышает установленной величины. Таким образом, применительно к широкополосным методам условие согласования можно представить в виде неравенства  относящегося к любой частоте диапазона.

Основными широкополосными согласующими устройствами являются широкополосные частотные компенсаторы, ступенчатые трансформаторы и неоднородные линии. Последние называют также плавными переходами.

Принцип частотной компенсации состоит во взаимной компенсации частотных изменений сопротивления нагрузки и согласующих элементов. Его можно осуществить за счет подбора необходимого закона частотного изменения сопротивления согласующих элементов и реализовать путем выбора длины и волнового сопротивления шлейфов и трансформаторов.

На рис. 3. 6, а показан один из вариантов широкополосного согласования комплексных нагрузок с помощью одного шлейфа. Пусть график входной проводимости согласуемой нагрузки 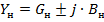 имеет вид, изображенный на рис. 3. 6, б. На этот же рисунок нанесен график входной проводимости согласующего шлейфа  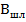, включенного по схеме рис. 3. 6, а.

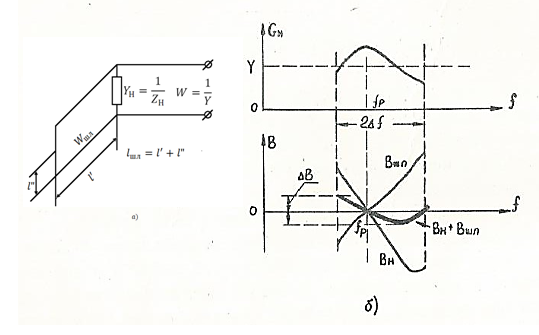
Рис. 3. 6. Согласование в полосе частот с помощью одного шлейфа:

а - схема согласующего устройства;

б - графики проводимости нагрузки и шлейфа

Наклон кривой 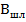 подобран примерно равным наклону кривой  с обратным знаком в пределах большей части заданной полосы частот. Поэтому суммарная реактивная проводимость 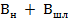 уменьшается и меньше изменяется с частотой, чем реактивная проводимость нагрузки. Наклон кривой  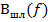прямо пропорционален длине шлейфа и обратно пропорционален его волновому сопротивлению  :

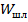где 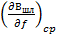 - среднее значение тангенса угла наклона кривой  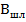; fp - резонансная частота.

Таким образом, подбором величины волнового сопротивления шлейфа или его длины  можно регулировать ширину полосы рабочих частот, в которой реактивная проводимость изменяется в допустимых пределах.

Активная составляющая проводимости нагрузки в рассматриваемой схеме остается без изменения. Несмотря на это, компенсация только реактивности дает требуемое повышение КБВ в заданной полосе частот: 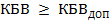 . В случае необходимости согласовать и активную составляющую можно установить четвертьволновый трансформатор.

Ступенчатые трансформаторы применяются для согласования линии с активной нагрузкой или нагрузкой, имеющей небольшую реактивную составляющую сопротивления, а также для соединения линий с различными волновыми сопротивлениями.

Ступенчатые трансформаторы представляют собой (рис. 3. 7, а) каскадное соединение n отрезков линии («ступенек»), имеющих одинаковую длину l и различные волновые сопротивления 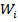. Общая длина перехода получается равной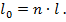

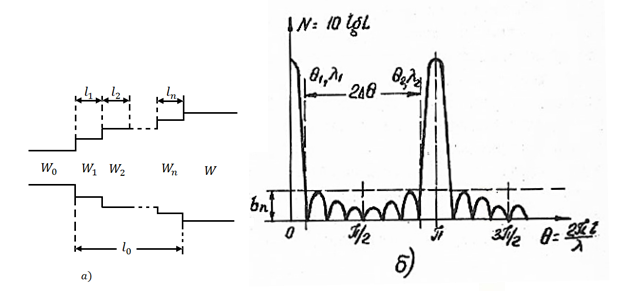
Рис. 3. 7. Ступенчатый трансформатор:

а - схема; б - зависимость рабочего затухания трансформатора от угла θ.

Под структурой ступенчатого трансформатора понимают распределение волновых сопротивлений ступенек 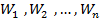 . Для выполнения расчетов вводят нормированные волновые сопротивления ступенек  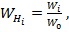где i - номер ступеньки;  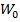- волновое сопротивление левой подводящей линии. При этом  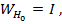а отношение  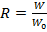представляет собой перепад волнового сопротивления.

Согласующие трансформаторы обычно характеризуют рабочим затуханием, которое представляет собой величину, обратную коэффициенту прохождения: 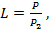 где Р - мощность на входе трансформатора;  - мощность в выходной линии при условии ее полного согласования на конце. Величина L > I и характеризует «затухание» в трансформаторе за счет отражения от него.

Основной характеристикой трансформатора является его частотная характеристика, представляющая собой зависимость рабочего затухания L от электрической длины ступеньки: 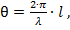 где λ - длина волны в ступеньке.

Зависимость рабочего затухания от θ обычно имеет вид некоторого полинома с косинусом в качестве аргумента

                                                                                          

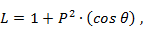
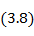
т. е. является периодической функцией по θ с периодом π (рис. 3. 7, б). Области изменения θ, где рабочее затухание мало, называют полосами пропускания, а где L велико - полосами заграждения. Практически используется лишь первая полоса пропускания (область между 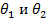 ), для которой длины ступенек получаются наименьшими при прочих равных условиях.

Форма частотных характеристик, описываемых уравнением (3. 8), характеризуется: шириной полосы пропускания 2Δ θ в электрических градусах или 2Δ f - в единицах частоты; допуском на рассогласование 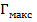- наибольшим допустимым значением коэффициента отражения в полосе пропускания; допустимым затуханием в полосе пропускания (вследствие отражения)

                                                                                              

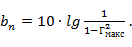
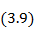
При расчете согласующего ступенчатого перехода исходными данными являются: перепад волнового сопротивления R, полоса пропускания 2Δ f, допуск на рассогласование  . Необходимо определить число ступенек n, их длину и волновые сопротивления; иными словами, требуется найти структуру трансформатора, обеспечивающего получение заданных характеристик.

Структура трансформатора определяет характер зависимости L в полосе пропускания, т. е. количество осцилляций, их расположение и относительный уровень. Среди различных возможных структур наибольшее распространение получили чебышевские ступенчатые трансформаторы и трансформаторы с максимально плоской частотной характеристикой. Вид частотных характеристик таких трансформаторов показан на рис. 3. 8, а, б.

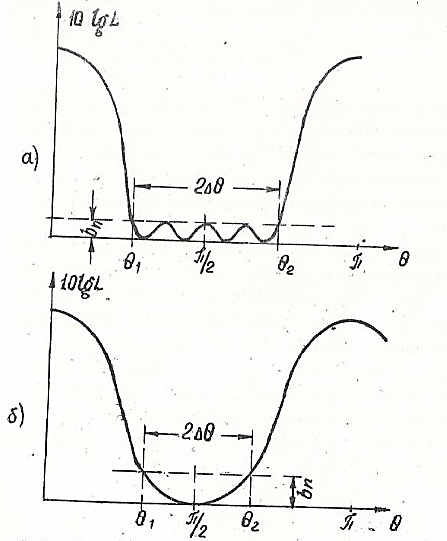
Рис. 3. 8. Частотные характеристики ступенчатых трансформаторов:

а - чебышевская характеристика; б - максимально плоская характеристика

В случае чебышевского трансформатора осцилляции («выбросы») затухания 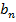 в полосе пропускания одинаковы по величине и достигаются (n+I) раз. В трансформаторе с максимально плоской частотной характеристикой допуск на рассогласование (величина 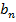) достигается лишь дважды - на краях полосы пропускания. Таким образом, заданные технические условия в чебышевских трансформаторах реализуются более экономным образом (т. е. при меньшем числе ступенек), что и определяет их оптимальность. Однако переход с максимально плоской частотной характеристикой обладает более линейной фазочастотной характеристикой.

Функция рабочего затухания чебышевского ступенчатого трансформатора имеет вид

                                                                                     

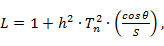
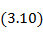
где n - число ступенек;

Tn -полином Чебышева первого рода n - го порядка.

Из основных свойств полиномов Чебышева известно, что 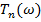 имеет колебательный характер на интервале -I ≤ ω ≤ +I, где изменяет свое значение в пределах ± I, и вне этого интервала быстро возрастает.

При переходе к ступенчатому трансформатору с чебышевской частотой характеристикой указанные амплитудные значения полиномов Чебышева 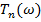 , равные ± I, должны быть увязаны с максимально допустимым значением модуля коэффициента отражения  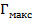в полосе пропускания трансформатора.

Аналогично интервал изменения аргумента полиномов Чебышева (-I ≤ ω ≤ +I) должен быть приведен в соответствие с полосой пропускания ступенчатого трансформатора.

Для этих целей в выражение (3. 10) введены нормирующий амплитудный множитель

                                                                                                          

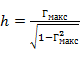
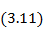
и нормирующий множитель S по оси частот

                                                                                       

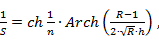
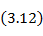
который зависит от числа ступенек трансформатора n, перепада волновых сопротивлений 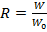 и h, т. е. от Гмакс.

Граничные длины волн из условия нормировки определяются выражениями

                                                                                     

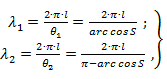
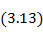
откуда связь между полосой пропускания и нормирующим множителем

                                                                        

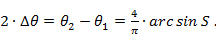
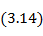
Используя приведенные формулы, можно произвести расчет трансформатора. Сначала по заданным крайним частотам полосы пропускания определяют величину полосы в электрических градусах 2Δ θ , а по ней - нормирующий множитель S (3. 14). С помощью (3. 11) по заданному допуску на рассогласование 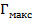 находят величину h. По заданному R и найденным значениям S и h с использованием соотношения (3. 12) получают число ступенек трансформатора

C учетом формул (3. 13) длина ступеньки определяется выражением

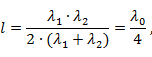
где  - длина волны в линии на некоторой частоте f0, называемой центральной.

В частном случае линии с волной ТЕМ 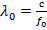 , т. е. частота f0 совпадает со средней частотой полосы пропускания.

Так как точный расчет распределения волновых сопротивлений между ступеньками известен только для трансформаторов с n ≤ 4, приведем расчетные формулы, например, для двухступенчатого трансформатора:

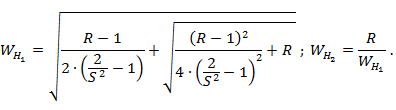
При n > 4 для расчетов волновых сопротивлений используют приближенные методы [I0].

Свойства ступенчатых трансформаторов с максимально плоской частотной характеристикой описываются функцией рабочего затухания вида

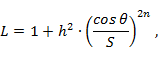
где n - число ступенек;

h и S - амплитудный и масштабный множители, имеющие тот же смысл, что и в случае чебышевского трансформатора.

Методика расчета перехода с максимально плоской характеристикой мало отличается от методики расчета чебышевского перехода. Поэтому останавливаться на нем не будем.

Следует учитывать, что при практическом конструировании ступенчатых переходов нет необходимости выполнять все этапы расчета, так как в справочной литературе имеются таблицы готовых результатов для различных типов переходов. Ступенчатые трансформаторы широко используются в полосковой технике.

Плавные переходы (трансформаторы), используемые при согласовании активных нагрузок, могут рассматриваться как предельный случай ступенчатых переходов при неограниченном увеличении числа ступенек и неизменной длине перехода  . Когда длина перехода соизмерима с длиной волны, электромагнитная энергия трансформируется из одной линии в другую с малыми отражениями.

Плавный переход, по существу, является неоднородной линией передачи, в которой погонные параметры и волновое сопротивление W(x) являются функцией продольной координаты (рис. 3. 9, а).

Расчет плавных переходов на основе точного решения телеграфных уравнений известен лишь для частных случаев распределения погонных параметров по длине линии, например экспоненциального. Однако такой переход не обладает оптимальными частотными характеристиками.

Экспоненциальным называется переход, волновое сопротивление которого изменяется вдоль продольной координаты х по экспоненциальному закону (рис. 3. 9, б). Это достигается изменением расстояния между проводами линии или их диаметра и соответственно изменением погонных индуктивности и емкости линии по ее длине.

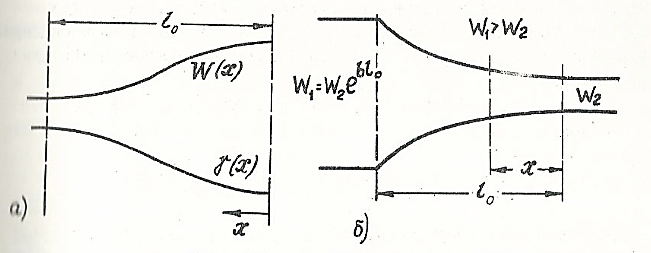
Рис. 3. 9. Плавный переход:

а, б - соответственно с произвольным и экспоненциальным законами изменения волнового сопротивления

Пусть погонные параметры линии меняются по длине по закону

где b - постоянная, характеризующая степень изменения параметров вдоль линии.

Обозначим погонные емкость и индуктивность в конце линии через 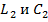 и будем считать линию идеальной. Тогда

и для волнового сопротивления экспоненциальной линии можно получить выражение

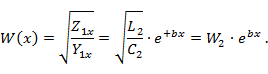
При постоянной b > 0 и увеличении x волновое сопротивление увеличивается (рис. 3. 9, б). Если b < 0, то по мере движения от конца линии к входу волновое сопротивление уменьшается.

Таким образом, экспоненциальная линия является диапазонным трансформатором, трансформирующим включенное на его конце активное сопротивление 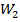 в активное сопротивление, равное  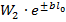. Эффективность такого согласующего трансформатора существенно зависит от степени изменения волнового сопротивления по длине линии. Чем меньше постоянная b, т. е. чем медленнее изменяются параметры линии, тем меньше отражение энергии от линии и КБВ ближе к единице.

Модуль коэффициента отражения на входе экспоненциального перехода

                                                                                               

Частотная характеристика такого перехода, т. е. зависимость 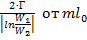 , показана на рис. 3. 10 (кривая I). Огибающая частотной характеристики, получающаяся из уравнения (3. 15), если в нем положить  , нанесена на том же рисунке пунктирной линией. Видим, что по мере увеличения отношения 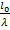 отражения от экспоненциального перехода уменьшаются.

Необходимую длину перехода можно найти из условия

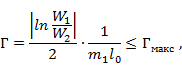
откуда

                                                                                                  

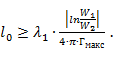
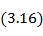
Недостатком плавных экспоненциальных переходов является их большая длина при значительных перепадах волнового сопротивления. Например, при 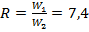 и допуске на рассогласование  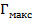≤ 0, 05 длина перехода согласно неравенству (3. 16)
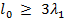 , где 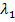 - длинноволновая граница рабочего диапазона (длина оптимального чебышевского перехода в 3-4 раза меньше).

К достоинствам такого перехода относятся простота расчета и изготовления. В случае коаксиального варианта экспоненциальный переход практически совпадает с линейным конусом. В полосковых линиях переход реализуется путем изменения ширины центрального полоскового проводника.

 

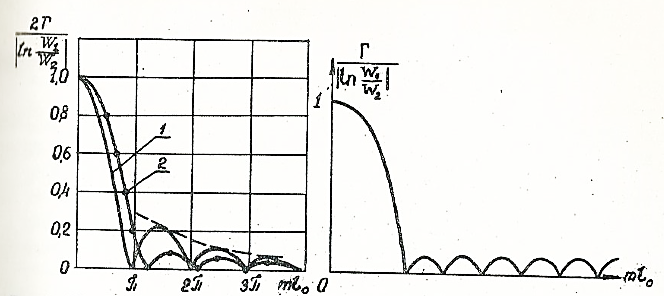
Рис. 3. 10 (слева). Частотные характеристики коэффициента отражения в плавных переходах: 1- экспоненциальный переход; 2- вероятностный переход

Рис. 3. 11 (справа). Частотная характеристика коэффициента отражения чебышевского плавного перехода

Среди плавных переходов наименьшую длину при одинаковых перепаде волновых сопротивлений, нижней граничной частоте и допуске на рассогласование имеют чебышевские переходы. Их параметры определяются из параметров ступенчатого трансформатора путем перехода к пределу при неограниченном возрастании числа ступенек n. Частотная характеристика входного коэффициента отражения плавного чебышевского перехода показана на рис. 3. 11.

Аналогично переход к пределу в ступенчатом переходе с максимально плоской характеристикой приводит к так называемому вероятностному плавному переходу. Частотная характеристика коэффициента отражения в вероятностных переходах приведена на рис. 3. 10 (кривая 2).

Сведения по расчету закона изменения волнового сопротивления в чебышевском и вероятностном плавных переходах и соответствующие таблицы содержатся в [I0].

Сравнение ступенчатых и плавных переходов показывает, что при одинаковых перепадах волновых сопротивлений и равных допусках на рассогласование в заданной полосе частот длина ступенчатого перехода заметно меньше, чем плавного. Однако при этом полоса пропускания плавного перехода гораздо шире. При повышенных требованиях к электрической прочности плавный переход предпочтительнее ступенчатого. Снижение электрической прочности последнего объясняется концентрацией электромагнитного поля в местах стыков отдельных ступенек.

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: