Уравнение взаимного ориентирования

Одной из важнейших задач фотограмметрии является взаимное ориентирование снимков. Основание для ее решения было предло­жено С. Финстервальдером в 1899 г. как условие пересечения в про­странстве пары соответственных лучей. Аналитическое решение зада­чи предложено профессором А.С. Скиридовым в 1928 г.

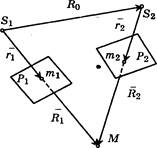
На рис. 9.9 изображена пара снимков Pi и Р2 и связки проектирую­щих лучей в том положении, которое они занимали в момент фотогра­фирования. Любая пара соотвегственных лучей (например, Sinti и S2^2) пересекается и находятся в одной плоскости, проходящей через базис фотографирования S1S2. При изменении положения одной из свя­зок проектирующих лучей соответственные лучи окажутся в разных плоскостях, в точке М не пересекутся, и модель разрушится.

Следовательно, условием взаимного ориентирования пары сним­ков является размещение соответственных векторов в одной базисной плоскости и их пересечение в одной точке. Математически это описы­вается условием компланарности векторов R\₉ Д2 и До > ^т- ^е- усло­вием равенства нулю их векторно-скалярного произведения, численно равного объему построенного на этих векторах параллелепипеда:

До х (Ri х Д₂) = 0.

Полученное условие связывает на­правления трех векторов, любой из которых можно разделить на свой мо­дуль, поэтому можно записать

До x(ri хг₂) = 0. (9.10)

Выражение (9.10) инвариантно по от­ношению к системе координат, в которой

Рис. 9.9. Условие взаимного ори ентирования снимков

представлены векторы До, п, гг, и в самом общем случае его можно записать в матричном виде следующим образом:

J59

^BX ^BY ^BZ

x\ y; z\ x\ y' z;

= o,

(9.11)

где, согласно рис. 9.4 и 9.8,

В_х = Б cost cos v, B_Y = В sin x cos v, B_z = Bsinv

(9.12)

Запишем условие (9.11) для рассмотренных выше систем элементов взаимного ориентирования.

В базисной системе элементов взаимного ориентирования (рис. 9.7) ось абсцисс координатной системы SiX'Y'Z' совпадает с базисом фотографирования, Вх = В, By = Bz = 0, и вместо (9.11) будем иметь:

в
№	Y{	Z[
*2	Y*	Z'2

о,

(9.13)

где в соответствии с (3.4)

z

\ = Цъ + Ъ'₂у_х - Щ1, Yi = 4*2 + b"₂y₂ - ЧЛ1 ₍₉.14)

1 ^{= c}i*i ^{+ c}2l/l ^{— с}3/> ^2 ^{= С}1^Х2 ^{+ С}2У2 ^— ^' J

Здесь В - базис фотографирования; X\?T\,Z'\ и Х'г^'г^'г ~ коор­динаты точек т\ и Ш2 в системах SjX'iY'iZ'i и йг-ХГ^Уг^'г; &'*» c'j, b"j, c"i (i = 1, 2, 3) - направляющие косинусы, определяемые по формулам (3.8) с заменой углов а, со, х элементами взаимного ориенти­рования ct'i, oo'i = 0, x'i для левого снимка и а'г, со'г, Х*2 ДЛ^Я правого.

Раскроем определитель (9.13) и разделим обе его части на вели­чину Б:

Y'iZ'a - Г2^1=0. (9.15)

Умножив это уравнение на (-f/Z'iZ^), после несложных преобра­зований с учетом (3.21) получим еще одну форму записи уравнения взаимного ориентирования в базисной системе

У?

У°2=Я° = 0,

(9.16)

интерпретируемую как условие равенства нулю поперечных парал­лаксов точек трансформированных снимков, или условие равенства их трансформированных ординат. Последнее и объясняет отсутствие

Поперечных параллаксов при стереоскопическом наблюдении эпи-полярных изображений.

Приведем уравнение (9.15) к линейному виду, представив эле­менты взаимного ориентирования в явном виде. Для этого заменим в формулах (3.8) тригонометрические функции углов а, со и х их разло­жениями в ряды с удержанием членов первого порядка малости

<h - ^b2 = ^сз =!» bi = ~^а2 = Ъ ^ci = ^_аз = ^а> ^с2 = ~^&з = -<°

и подставим эти значений в (9.14) и (9.15) с заменой а, со, % на элементы взаимного ориентирование левого и правого снимков:

(Xi*i + J/i)(<*2*2 + го'гУг - Л - (Хг*2 + У 2 + ю'гЖа'Л " /) = ° •

Раскроем скобки, примем i/i = 1/2 ⁼ У ^и после простых преобразо­ваний получим уравнение взаимного ориентирования в линейном ви­де:

Ш_а>_г _ Ы^ _ _{(/ +} У1щ _{+ XlXi} _ ^ ₊ д = 0. (9.17)

В линейно-угловой системе элементов взаимного ори­ентирования (рис. 9.8) принята система координат левого снимка S\xyz, составляющие базиса фотографирования определяются формулами (9.12), а фотограмметрические координаты точек левого снимка соответствуют измеренным. С учетом этого вместо (9.11) бу­дем иметь, разделив первую строку на В_х: |1 tgx' tgv'/cosi'l

= 0, (9.18)

К ^у} ~/

Р^2 ^2 ^2

Где

Yi = Цх₂ + Щу₂ - Щ Z₂ = c{x₂ + <?₂y₂-c"_sfj'

т' и v' - углы поворота и наклона базиса фотографирования в линейно-угловой системе элементов взаимного ориентирования; х\, z/i, Хг₉ yi -координаты точки на левом и правом снимках; ftf, c\ (i = 1, 2, 3) - на­правляющие косинусы, определяемые по формулам (3.8) с заменой в них углов а, со и х элементами взаимного ориентирования Да, Дсо и Ах-Раскрыв определитель (9.18), после приведения его к линейному виду рассмотренным выше способом и полагая у\ = z/2 ⁼ У* получим

Зак. 344

. рх' + ^v' + ^/Дсс + (/ + ^)Асо + х₂Ах - g = 0. (9.19)

Уравнения (9.17) и (9.19) пригодны для определения элементов взаимного ориентирования только плановых снимков. Для этого изме­ряют координаты и параллаксы как минимум пяти точек, составляют для каждой из них уравнение (9.17) или (9.19) и решают полученную систему уравнений.

⇐ Предыдущая28293031323334353637Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: