Магнитное поле в веществе. Виды магнетиков.
Гипотеза Ампера о молекулярных токах. Вектор намагничивания.
Различные вещества в той или иной степени способны к намагничиванию: то есть под действием магнитного поля, в которое их помещают, приобретать магнитный момент. Одни вещества намагничиваются сильнее, другие слабее. Будем называть все эти вещества магнетиками.
Для объяснения способности тел к намагничиванию, Ампер предположил, что в молекулах вещества циркулируют круговые токи (получившие впоследствии название молекулярных токов Ампера). Каждый такой ток обладает собственным магнитным моментом  и создает в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля токи Ампера ориентированы беспорядочным образом, вследствие чего обусловленное ими магнитное поле равно нулю. Суммарный магнитный момент тела также равен нулю (рис.11.1).
и создает в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля токи Ампера ориентированы беспорядочным образом, вследствие чего обусловленное ими магнитное поле равно нулю. Суммарный магнитный момент тела также равен нулю (рис.11.1).

Рис.11.1. Молекулярные токи Ампера. Намагничивание вещества.
Под действием внешнего магнитного поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается, а его суммарный магнитный момент становится отличным от нуля (см. рис.11.1).
Для характеристики степени намагниченности вещества используют величину 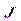 , называемую вектором намагничивания (или намагниченности). По определению:
, называемую вектором намагничивания (или намагниченности). По определению:
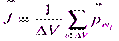 ,
,
где суммирование производится по всем молекулам, принадлежащим данному объему ΔV.
Описание магнитного поля в магнетиках. Напряженность и индукция магнитного поля. Магнитная восприимчивость и магнитная проницаемость вещества.
Намагниченное вещество создает магнитное поле  , которое накладывается на внешнее поле
, которое накладывается на внешнее поле 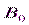 (поле в вакууме). Оба поля в сумме дают результирующее магнитное поле с индукцией
(поле в вакууме). Оба поля в сумме дают результирующее магнитное поле с индукцией
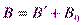 ,
,
причем под 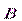 здесь и далее подразумевается макроскопическое (усредненное по физически бесконечно малому объему вещества) поле.
здесь и далее подразумевается макроскопическое (усредненное по физически бесконечно малому объему вещества) поле.
В силу замкнутости силовых линий полей  и
и 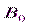 , поток результирующего поля
, поток результирующего поля 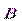 через произвольную замкнутую поверхность S равен нулю:
через произвольную замкнутую поверхность S равен нулю:

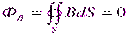 .
.
Таким образом, теорема Гаусса в применении к магнетикам имеет такой же вид, как и в вакууме.
Обратимся теперь к циркуляции вектора 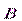 по замкнутому контуру. Согласно теореме о циркуляции магнитного поля:
по замкнутому контуру. Согласно теореме о циркуляции магнитного поля:
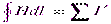 или
или 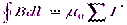 ,
,
где под  следует понимать теперь сумму как макроскопических, так и молекулярных токов, то есть
следует понимать теперь сумму как макроскопических, так и молекулярных токов, то есть
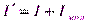 .
.
Сумма всех молекулярных токов, охваченных контуром интегрирования, есть:
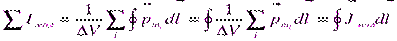 .
.
Следовательно, можем написать:
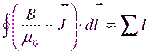 .
.
Величину, стоящую в круглых скобках под знаком интеграла, обозначают буквой  и называют напряженностью магнитного поля:
и называют напряженностью магнитного поля:

 .
.
Теперь мы можем записать теорему о циркуляции магнитного поля как:
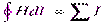 ,
,
где под 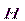 понимается введенная выше величина, характеризующая напряженность магнитного поля в веществе.
понимается введенная выше величина, характеризующая напряженность магнитного поля в веществе.
Согласно написанному равенству, циркуляция вектора напряженности магнитного поля по некоторому замкнутому контуру равна алгебраической сумме макроскопических токов, охваченных этим контуром.
Из сказанного следует, что вектор 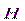 является аналогом вектора электрической индукции
является аналогом вектора электрической индукции  . Первоначально предполагалось, что в природе имеются подобные электрическим зарядам «магнитные заряды», и учение о магнетизме развивалось по аналогии с учением об электричестве. Тогда же были введены названия «электрическая индукция» для
. Первоначально предполагалось, что в природе имеются подобные электрическим зарядам «магнитные заряды», и учение о магнетизме развивалось по аналогии с учением об электричестве. Тогда же были введены названия «электрическая индукция» для 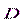 и «магнитная индукция» для
и «магнитная индукция» для 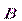 . Позже, однако, выяснилось, что в природе «магнитных зарядов» нет и в действительности магнитная индукция
. Позже, однако, выяснилось, что в природе «магнитных зарядов» нет и в действительности магнитная индукция 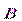 является аналогом не
является аналогом не 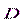 , а напряженности электрического поля
, а напряженности электрического поля 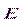 ; соответственно напряженность магнитного поля
; соответственно напряженность магнитного поля  – аналогом индукции электрического поля
– аналогом индукции электрического поля  .
.
Итак, индукция магнитного поля есть:
 .
.
Вектор намагничивания 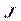 принято связывать не с магнитной индукцией
принято связывать не с магнитной индукцией 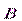 , а с напряженностью магнитного поля
, а с напряженностью магнитного поля 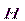 , и как показывает опыт, вектор
, и как показывает опыт, вектор  связан с вектором
связан с вектором  соотношением:
соотношением:
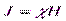 ,
,
где χ – характерная для данного магнетика величина, называемая магнитной восприимчивостью.
Поскольку  имеет ту же размерность, что и
имеет ту же размерность, что и 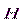 [A/м], то χ – безразмерная величина. На основании двух последних формул имеем:
[A/м], то χ – безразмерная величина. На основании двух последних формул имеем:
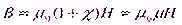 ,
,
где через

обозначена величина, называемая магнитной проницаемостью.
Классификация магнетиков.
В то время как диэлектрическая проницаемость ε у всех веществ всегда больше единицы (диэлектрическая восприимчивость κ >0), магнитнаяпроницаемость μ может быть как больше единицы, так и меньше единицы (соответственно магнитная восприимчивость χ >0 и χ <0). Поэтому магнитные свойства веществ отличаются гораздо большим разнообразием, чем электрические свойства.
| ^ Тип магнетика
| Магнитная восприимчивость, χ
|
| Диамагнетик
| - (10-9 – 10-4), μ<1
|
| Парамагнетик
| 10-6 – 10-3, μ>1
|
| Ферромагнетик
| 103 – 105, μ(Н)>>1
|
| Ферримагнетик
| 101 – 103, μ(Н)>>1
|
| Антиферромагнетик
| 10-4 – 10-6, μ>1
|
| Сверхдиамагнетик
| - 1, μ=0
|
Дадим краткую характеристику каждого типа магнетика.
Диамагнетики – вещества, характеризуемые отрицательным значением магнитной восприимчивости χ. Вследствие этого вектор намагничивания  в этих веществах направлен противоположно внешнему намагничивающему полю
в этих веществах направлен противоположно внешнему намагничивающему полю 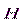 . Диамагнетиками являются, например, вода (χ = - 9∙10-6), серебро (χ = - 2,6∙10-5), висмут (χ = - 1,7∙10-4).
. Диамагнетиками являются, например, вода (χ = - 9∙10-6), серебро (χ = - 2,6∙10-5), висмут (χ = - 1,7∙10-4).
Парамагнетики – характеризуются положительным значение χ, ведут они себя подобно диэлектрикам с диэлектрической проницаемостью ε >1, то есть вектор  в этих веществах параллелен намагничивающему полю
в этих веществах параллелен намагничивающему полю  . К парамагнетикам относятся алюминий (χ = 2,1∙10-6), платина (χ = 3∙10-4), хлористое железо (χ = 2,5∙10-3).
. К парамагнетикам относятся алюминий (χ = 2,1∙10-6), платина (χ = 3∙10-4), хлористое железо (χ = 2,5∙10-3).
Ферромагнетики – особый вид магнетиков, отличающийся от других магнетиков следующими характерными признаками: 1) высоким значением магнитной восприимчивости (см. таблицу); 2) зависимостью магнитной проницаемости μ от напряженности магнитного поля, вследствие чегозависимость  от
от 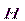 для этих веществ является нелинейной; 3) наличием петли гистерезиса на кривой намагничивания; 4) существованием температуры, называемой точкой Кюри, выше которой ферромагнетик ведет себя как обычный парамагнетик. Из чистых металлов ферромагнетиками являются железо, никель, кобальт, а также некоторые редкоземельные металлы (например, гадолиний). К числу ферромагнетиков относятся сплавы и соединения этих металлов, а также сплавы и соединения марганца и хрома с неферромагнитными элементами (например, MnAlCu, CrTe и другие).
для этих веществ является нелинейной; 3) наличием петли гистерезиса на кривой намагничивания; 4) существованием температуры, называемой точкой Кюри, выше которой ферромагнетик ведет себя как обычный парамагнетик. Из чистых металлов ферромагнетиками являются железо, никель, кобальт, а также некоторые редкоземельные металлы (например, гадолиний). К числу ферромагнетиков относятся сплавы и соединения этих металлов, а также сплавы и соединения марганца и хрома с неферромагнитными элементами (например, MnAlCu, CrTe и другие).
Ферримагнетики (ферриты) – вещества, в которых магнитные моменты атомов кристаллической решетки образуют несколько магнитных подрешеток с магнитными моментами, направленными навстречу друг другу. Имея меньшую величину магнитной восприимчивости по сравнению с ферромагнетиками, в остальном ферримагнетики характеризуются теми же признаками, что и ферромагнетики. Типичными ферритами являются соединения оксидов железа с оксидами других металлов - шпинели (MnFe2O4), гранаты Gd3Fe5O12), гексаферриты (PbFe12O19). Другую группу ферритов образуют двойные фториды типа RbNiF3, а также соединения типа RFe2 (R – редкоземельный металл).
Антиферромагнетики – частный случай ферримагнетиков, в которых магнитные моменты подрешеток с противоположно направленными магнитными моментами полностью компенсируют друг друга (скомпенсированный ферримагнетик). Существование антиферромагнетиков было предсказано Л.Д.Ландау в 1933г. В настоящее время известен широкий спектр веществ, обладающих антиферромагнитными свойствами: редкоземельные элементы (Er, Dy, Ho), оксиды и дифториды некоторых металлов (FeO, MnO, CoF2, NiF2), соли угольной и серной кислот (MnCO3, NiSO4) и другие.
Сверхдиамагнетики (идеальные диамагнетики) – вещества, магнитная прони-цаемость μ которых равна нулю. Благодаря этой особенности для сверхдиамагнетиков имеет место эффект Мейсснера-Оксенфельда (Meissner W., 1882-1974; Ocksenfeld C.) – полное выталкивание магнитного поля из объема сверхдиамагнетика (магнитная индукция  =0). Сверхдиамагнетиками являются все вещества, находящиеся в сверхпроводящем состоянии - низкотемпературные сверхпроводники (металлы) и высокотемпературные сверхпроводники (керамики). Из несверхпроводящих материалов, обладающих сверхдиамагнитными свойствами, известен пока только один пример – хлорид меди (CuCl), открытый в 1986г. (Русаков А.П., МИСиС).
=0). Сверхдиамагнетиками являются все вещества, находящиеся в сверхпроводящем состоянии - низкотемпературные сверхпроводники (металлы) и высокотемпературные сверхпроводники (керамики). Из несверхпроводящих материалов, обладающих сверхдиамагнитными свойствами, известен пока только один пример – хлорид меди (CuCl), открытый в 1986г. (Русаков А.П., МИСиС).
Воспользуйтесь поиском по сайту:


 и создает в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля токи Ампера ориентированы беспорядочным образом, вследствие чего обусловленное ими магнитное поле равно нулю. Суммарный магнитный момент тела также равен нулю (рис.11.1).
и создает в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля токи Ампера ориентированы беспорядочным образом, вследствие чего обусловленное ими магнитное поле равно нулю. Суммарный магнитный момент тела также равен нулю (рис.11.1).
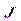 , называемую вектором намагничивания (или намагниченности). По определению:
, называемую вектором намагничивания (или намагниченности). По определению: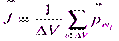 ,
, , которое накладывается на внешнее поле
, которое накладывается на внешнее поле 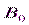 (поле в вакууме). Оба поля в сумме дают результирующее магнитное поле с индукцией
(поле в вакууме). Оба поля в сумме дают результирующее магнитное поле с индукцией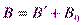 ,
,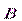 здесь и далее подразумевается макроскопическое (усредненное по физически бесконечно малому объему вещества) поле.
здесь и далее подразумевается макроскопическое (усредненное по физически бесконечно малому объему вещества) поле. и
и 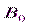 , поток результирующего поля
, поток результирующего поля 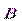 через произвольную замкнутую поверхность S равен нулю:
через произвольную замкнутую поверхность S равен нулю:
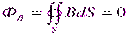 .
.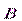 по замкнутому контуру. Согласно теореме о циркуляции магнитного поля:
по замкнутому контуру. Согласно теореме о циркуляции магнитного поля: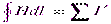 или
или 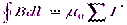 ,
, следует понимать теперь сумму как макроскопических, так и молекулярных токов, то есть
следует понимать теперь сумму как макроскопических, так и молекулярных токов, то есть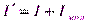 .
.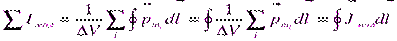 .
.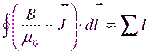 .
. и называют напряженностью магнитного поля:
и называют напряженностью магнитного поля: 
 .
.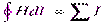 ,
,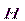 понимается введенная выше величина, характеризующая напряженность магнитного поля в веществе.
понимается введенная выше величина, характеризующая напряженность магнитного поля в веществе.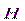 является аналогом вектора электрической индукции
является аналогом вектора электрической индукции  . Первоначально предполагалось, что в природе имеются подобные электрическим зарядам «магнитные заряды», и учение о магнетизме развивалось по аналогии с учением об электричестве. Тогда же были введены названия «электрическая индукция» для
. Первоначально предполагалось, что в природе имеются подобные электрическим зарядам «магнитные заряды», и учение о магнетизме развивалось по аналогии с учением об электричестве. Тогда же были введены названия «электрическая индукция» для 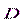 и «магнитная индукция» для
и «магнитная индукция» для 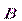 . Позже, однако, выяснилось, что в природе «магнитных зарядов» нет и в действительности магнитная индукция
. Позже, однако, выяснилось, что в природе «магнитных зарядов» нет и в действительности магнитная индукция 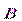 является аналогом не
является аналогом не 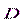 , а напряженности электрического поля
, а напряженности электрического поля 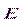 ; соответственно напряженность магнитного поля
; соответственно напряженность магнитного поля  – аналогом индукции электрического поля
– аналогом индукции электрического поля  .
. .
.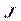 принято связывать не с магнитной индукцией
принято связывать не с магнитной индукцией 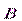 , а с напряженностью магнитного поля
, а с напряженностью магнитного поля 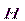 , и как показывает опыт, вектор
, и как показывает опыт, вектор  связан с вектором
связан с вектором  соотношением:
соотношением: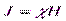 ,
, имеет ту же размерность, что и
имеет ту же размерность, что и 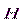 [A/м], то χ – безразмерная величина. На основании двух последних формул имеем:
[A/м], то χ – безразмерная величина. На основании двух последних формул имеем: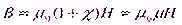 ,
,
 в этих веществах направлен противоположно внешнему намагничивающему полю
в этих веществах направлен противоположно внешнему намагничивающему полю 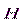 . Диамагнетиками являются, например, вода (χ = - 9∙10-6), серебро (χ = - 2,6∙10-5), висмут (χ = - 1,7∙10-4).
. Диамагнетиками являются, например, вода (χ = - 9∙10-6), серебро (χ = - 2,6∙10-5), висмут (χ = - 1,7∙10-4). в этих веществах параллелен намагничивающему полю
в этих веществах параллелен намагничивающему полю  . К парамагнетикам относятся алюминий (χ = 2,1∙10-6), платина (χ = 3∙10-4), хлористое железо (χ = 2,5∙10-3).
. К парамагнетикам относятся алюминий (χ = 2,1∙10-6), платина (χ = 3∙10-4), хлористое железо (χ = 2,5∙10-3). от
от 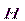 для этих веществ является нелинейной; 3) наличием петли гистерезиса на кривой намагничивания; 4) существованием температуры, называемой точкой Кюри, выше которой ферромагнетик ведет себя как обычный парамагнетик. Из чистых металлов ферромагнетиками являются железо, никель, кобальт, а также некоторые редкоземельные металлы (например, гадолиний). К числу ферромагнетиков относятся сплавы и соединения этих металлов, а также сплавы и соединения марганца и хрома с неферромагнитными элементами (например, MnAlCu, CrTe и другие).
для этих веществ является нелинейной; 3) наличием петли гистерезиса на кривой намагничивания; 4) существованием температуры, называемой точкой Кюри, выше которой ферромагнетик ведет себя как обычный парамагнетик. Из чистых металлов ферромагнетиками являются железо, никель, кобальт, а также некоторые редкоземельные металлы (например, гадолиний). К числу ферромагнетиков относятся сплавы и соединения этих металлов, а также сплавы и соединения марганца и хрома с неферромагнитными элементами (например, MnAlCu, CrTe и другие). =0). Сверхдиамагнетиками являются все вещества, находящиеся в сверхпроводящем состоянии - низкотемпературные сверхпроводники (металлы) и высокотемпературные сверхпроводники (керамики). Из несверхпроводящих материалов, обладающих сверхдиамагнитными свойствами, известен пока только один пример – хлорид меди (CuCl), открытый в 1986г. (Русаков А.П., МИСиС).
=0). Сверхдиамагнетиками являются все вещества, находящиеся в сверхпроводящем состоянии - низкотемпературные сверхпроводники (металлы) и высокотемпературные сверхпроводники (керамики). Из несверхпроводящих материалов, обладающих сверхдиамагнитными свойствами, известен пока только один пример – хлорид меди (CuCl), открытый в 1986г. (Русаков А.П., МИСиС).

