 |
Поля (скалярные и векторные)
|
|
|
|
Скалярным полем называют пространство, каждой точке которого ставится в соответствие скалярная величина, например температурное поле, распределение плотности, заряда, потенциала и т. д. Скалярные поля удобно отображать в виде поверхностей уровня, на которых поле обладает постоянным значением. Если каждой точке пространства ставится в соответствии вектор, то говорят о векторном поле (например, поле электрической и магнитной напряженности, поле скоростей течения жидкости). Для наглядности представления векторных полей используют линии тока. Это кривые, в каждой точке которых вектор поля есть касательный вектор.
Градиентом скалярного поля U называют вектор (обозначаемый grad U), определяемый в каждой точке поля соотношением
.
где: i, j, k – единичные вектора для осей x, y, z соответственно.
Часто вектор grad U обозначают также 
или 
.
Градиент потенциала электростатического поля – это напряженность поля:
. (11.8)
Если для векторного поля V (r) существует функция U (r) такая, что 
, то U (r) называется потенциалом векторного поля V (r), а само поле – потенциальным или консервативным.
Дивергенцией (div V) векторного поля V (r) называют скалярную величину
.
Дивергенция есть мера источников поля. Если, например, в вакууме имеются заряды с плотностью заряда ρ, то напряженность электрического поля E, создаваемая этими зарядами, удовлетворяет уравнению
, (11.9)
где ε0 – диэлектрическая постоянная.
Если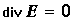 
, значит, в этой точке поля заряды отсутствуют, в ней нет источников поля E.
Понятие ротора (rot V) векторного поля V можно ввести при помощи понятия циркуляции векторного поля: 
вдоль замкнутой кривой C.
В консервативном векторном поле всегда Г = 0. Если для векторного поля существуют замкнутые линии тока, то циркуляция векторного поля вдоль этих линий не будет равна нулю. Циркуляция есть мера завихренности поля. Для нахождения ротора векторного поля определяют отношение циркуляции векторного поля вдоль контура к площади, охватываемой контуром, когда диаметр этой площади стремится к нулю. Предел этого отношения есть ротор векторного поля.
|
|
|
В координатном представлении
.
Для стационарного электрического и магнитного поля:
, 
, 
, 
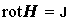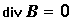. (11.10)
Кроме того, для всех сред имеются материальные уравнения, которые в случае изотропных, неферромагнитных и несегнетоэлектрических сред имеют самый простой вид.
Уравнения Максвелла
Обобщив основные законы электрических и магнитных явлений: теоремы Остроградского-Гаусса, законов полного тока и электромагнитной индукции Максвелл создал теорию, позволяющую решать задачи, связанные с отысканием электрических и магнитных полей, создаваемых заданным распределением зарядов и токов. Согласно этой теории, переменное магнитное поле создает вихревое электрическое, как и переменное, электрическое порождает вихревое магнитное поле.
Теория Максвелла представляет собой систему уравнений, в которой свойства среды описываются с помощью трех величин: относительной диэлектрической проницаемости ε, относительной магнитной проницаемости m и удельной электропроводности g.
Первое уравнение Максвелла в интегральной форме представляет собой закон электромагнитной индукции:
. (11.11)
Если в уравнении (11.11) длина контура L стремится к нулю, то его можно привести к виду:
. (11.12)
Это первое уравнение Максвелла в дифференциальной форме.
Второе уравнение Максвелла в интегральной форме является законом полного тока:
, (11.13)
где Ik – k-й ток, пронизывающий контур L; Iсм – ток смещения.
Второе уравнение Максвелла в дифференциальной форме:
|
|
|
. (11.14)
Помимо уравнений (11.12) и (11.14) в систему уравнений Максвелла входит теорема Остроградского-Гаусса для электрического и магнитного полей:
, (11.15)
. (11.16)
Уравнение (11.16) выражает факт отсутствия свободных магнитных зарядов. Если ввести объемную плотность свободных зарядов r и учесть теорему Гаусса: 
, где dV – элемент объема V, можно получить третье и четвертое уравнения Максвелла в дифференциальной форме:
, (11.17)
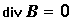. (11.18)
Полная система уравнений Максвелла:
, ,
,
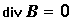
дополняется материальными уравнениями, связывающими векторы E, D, H и B с величинами, описывающими электрические и магнитные свойства среды:
, 
, 
. (11.19)
При заданных начальных условиях система уравнений Максвелла имеет единственное решение.
Теория Максвелла не только объяснила уже известные факты, но и предсказала новые явления. Максвелл теоретически предсказал существование электромагнитных волн, распространяющихся в пространстве с конечной скоростью, что в дальнейшем получило блестяще подтверждение.
Явление самоиндукции.
Ток I, текущий в любом контуре, создает магнитный поток Ф, пронизывающий этот же контур. При изменении I будет изменяться Ф. Следовательно, в контуре будет наводиться ЭДС индукции.
Т.к. магнитная индукция В пропорциональна току I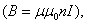 
следовательно
где L – коэффициент пропорциональности, названный индуктивностью контура.
Если внутри контура нет ферромагнетиков, то 
(т.к. 
).
Индуктивность контура L зависит от геометрии контура, числа витков, площади витка контура.
За единицу индуктивности в СИ принимается индуктивность такого контура, у которого при токе 
возникает полный поток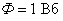 
. Эта единица называется Генри (Гн).
Размерность индуктивности:
Вычислим индуктивность соленоида L. Если длина соленоида l гораздо больше его диаметра d ( 
), то к нему можно применить формулы для бесконечно длинного соленоида. Тогда
здесь N – число витков. Поток через каждый из витков 
Потокосцепление
Но мы знаем, что 
, откуда индуктивность соленоида
где n – число витков на единицу длины, т.е. 
– объем соленоида, значит
 ,
| (5.1.1) |
Из этой формулы можно найти размерность для магнитной постоянной:
При изменении тока в контуре возникает ЭДС самоиндукции, равная:
|
|
|
 ,
| (5.1.2) |
Знак минус в этой формуле обусловлен правилом Ленца.
Явление самоиндукции играет важную роль в электротехнике и радиотехнике. Как мы увидим дальше, благодаря самоиндукции происходит перезарядка конденсатора, соединенного последовательно с катушкой индуктивности, в результате в такой LC -цепочке (колебательном контуре) возникают электромагнитные колебания.
|
|
|
