 |
Вихревое электрическое поле. Первое уравнение Максвелла.
|
|
|
|
Рассматривая свойства электростатического поля, отмечалось, что работа по перемещению заряда из одной точки поля в другую не зависит от пути. Поле с таким свойством называют потенциальным. Отношение работы по перемещению положительного заряда из бесконечности в какую-либо точку называют потенциалом этой точки, а разность потенциалов двух точек – электрическим напряжением. В электростатическом поле E работа по перемещению единичного заряда по замкнутому контуру L равна нулю (рис. 11.1):
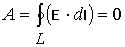
Такой интеграл называют циркуляцией напряженности по замкнутому контуру L. Предел отношения циркуляции векторного поля по замкнутому контуру к площади охватываемого контуром при стремлении ее к нулю называют ротором (rot) векторного поля. Для электростатического поля
rot E = 0.
Анализируя результаты опытов Фарадея, Максвелл установил, что эдс электромагнитной индукции, возникающая в контуре, пропорциональна скорости изменения магнитного потока, охватываемого этим контуром:
. (11.1)
Опыты показали, что эдс индукции не зависит от материала проводника, его состояния и температуры. Максвелл пришел к выводу, что причиной возникновения электромагнитной индукции является само электрическое поле, а проводники играют второстепенную роль и служат только прибором, обнаруживающим это поле. Электроны в проводнике под действием этого поля приходят в движение, и в замкнутой цепи контура возникает индукционный ток.
Электрическое поле, возникающее в опытах по электромагнитной индукции, не удовлетворяет условию потенциальности. Особенность этого электрического поля в том, что оно не является электростатическим.
Линии напряженности его не начинаются и не заканчиваются на электрических зарядах. Линии напряженности электрического поля, возникающего при электромагнитной индукции, образуют замкнутые кривые. Такое поле называют вихревым электрическим полем.
|
|
|
При изменении магнитного поля в какой-либо точке всегда можно найти контур, в котором возникнет эдс индукции, а следовательно, и вихревое электрическое поле. Рассмотрев эти явления, Максвелл пришел к выводу, что всякое изменение магнитного поля вызывает появление электрического поля.
Для магнитного потока, пронизывающего контур l, площадью S (рис. 11.1) можно записать соотношение
, (11.2)
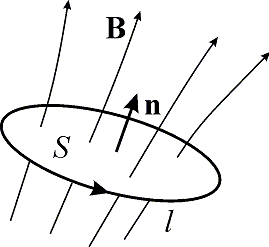
Рис. 11.1. Контур, охватывающий магнитный поток
где Bn – проекция вектора магнитной индукции на ось, параллельную нормали n к элементарной площадке dS.
Кроме того, эдс индукции по замкнутому контуру:
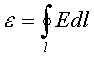. (11.3)
Объединяя уравнения (11.1) и (11.3) получим:
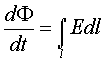. (11.4)
Это соотношение выражает связь между вихревым электрическим (E) и переменным магнитным полем (B) и является одним из основных уравнений в теории Максвелла (основной закон электромагнитной индукции).
Ток смещения
Рассматривая прохождение переменного электрического тока в цепи, содержащей конденсатор (рис. 11.2) можно заметить, что конденсатор не препятствует прохождению электрического тока, этот ток обеспечивается изменением заряда на обкладках конденсатора. Окружим одну из обкладок конденсатора воображаемой замкнутой поверхностью S. В течение интервала времени dt от источника переменного напряжения по проводнику через эту поверхность переместится заряд dq. По теореме Гаусса поток вектора электрического смещения сквозь замкнутую поверхность равен сумме свободных зарядов, находящихся внутри этой поверхности:
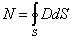. (11.5)
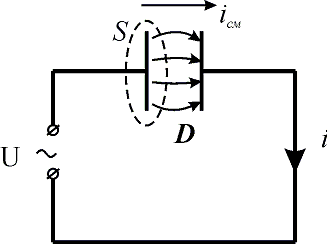
Рис. 11.2. Прохождение переменного электрического тока через конденсатор
Изменение потока электрического смещения за время dt равно изменению заряда:
|
|
|
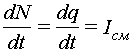. (11.6)
Максвелл назвал величину Iсм током смещения. В соответствии с этим представлением цепь, приведенная на (рис. 11.2), замыкается в конденсаторе током смещения.
Найдем плотность тока смещения Iсм на поверхности S:
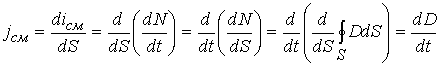. (11.7)
Максвелл пришел к заключению, что всякое изменение электрического поля вызывает появление магнитного поля, эквивалентного полю, создаваемому токами проводимости.
В соответствии с законом полного тока, циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром. Для плоского конденсатора в области однородного поля
,
где H – напряженность магнитного поля по длине контура L; Iпр – ток проводимости диэлектрика; jсмS – ток смещения через поверхность S, охватываемую контуром.
Для дальнейшего описания теории Максвелла рассмотрим некоторые элементы теории поля.
|
|
|
