Основы статистических методов анализа и расчета

Таблицы

Первичные наблюдения, поученные в результате регистрации или измерения параметров варьирующего ряда значений, необходимо пред­ставить в каком то упорядоченном виде. Наиболее простой вид такого представления – это статистические таблицы. В статистических табли­цах данные систематизируются по разным признакам, это может быть время, отделы организации, отдельные работники, виды дефектов и т.д.

Графики

а) Круговые диаграммы. Один из самых широко используемых вариантов визуального представления данных, потому что их легко чи­тать и понимать. Круговая диаграмма берет категорийные данные и де­лит их на категории, группы, показывая процентное отношение единиц в каждой группе. Круговая диаграмма показывает нам, долю каждой группы в общей массе, которая составляет 100%. Эта диаграмма служит для сравнения групп. Это очень важно при выявлении основных групп, составляющих основу всей массы статистических данных.

Пример. Группа ученых ведет социологическое исследование- изучается источники информации среди молодежи. Проведен опрос: «Главный источник информации для Вас?». Выбрано 2 категории респондентов: от 15 до 20 лет, от 20 до 25 лет. В каждой группе 200 человек. Получены ответы, которые сведены в таблицу 7.1.

 

Таблица 7. 1.

№№		Источник		Возраст, лет
				От 15 до 20		От 20 до 25
		интернет
		телевидение
		Учебное заведение
		Окружающие люди
		книги
		Итого:

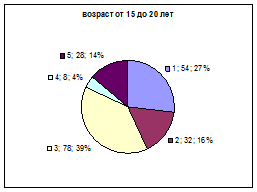А)

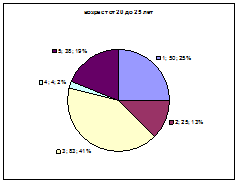Б)

Рисунок 7.1.- А- младшая, Б- старшая группы

 

На диаграмме (Рисунок 7.1.) хорошо видно, что главный источник информации является учебное заведение, но у старшей группы это источник более важный. Меньше всего информации получают от окружающих людей, причем в старшей группе это показатель уменьшился в 2 раза. Книги у старшей группы имеют большее значение, чем в младшей.

б) Столбиковые диаграммы. Эти диаграммы самый распростра­ненный вид визуального представления общих данных производства. Здесь данные также делятся на группы и количественные данные каж­дой группы показываются в виде столбиков разной высоты. В основном столбиковые диаграммы хорошо применять, когда надо в динамике от­следить изменение параметра во времени. Но они хорошо смотрятся и при показе величины параметра относительно другого.

Пример На заводе исследуется рост выпуска готовой продукции и повышению уровня бездефектной продукции за последние 5 лет. Данные имеются в табличной форме, но их можно параллельно представить в виде диа­граммы.

 

Таблица 7.2.

год	Количество вы­пущенных трак­торов, тыс. шт	Количество трак­торов, сданных с первого раза, тыс. шт.	% годных тракторов, сданных с пер­вого раза
	42,2	38,9	92,18
	45,6	42,4	92,98
	55,1	52,3	94,92
	48,6	47,1	96,91
	66,9	64,8	96,86

Рисунок 7.2.

 

На диаграмме 7.2. хорошо видно, что в 2010 году был спад производ­ства, но качество продукции, имеет стойкую тенденцию к повышению.

в) Временная диаграмма (линейный график) – это вариант визуаль­ного представления данных, основная задача которого – проследить за тенденциями, происходящими за определенный период времени. По оси абсцисс откладывается время, а по оси ординат откладываются значения исследуемого параметра. На такой диаграмме удобно следить, как меня­ется параметр во временной динамике.

Пример. Руководство банка хочет узнать, количество работников, которые опаздывают на работу, причем учет необходим по отделам. Ра­ботник считается опоздавшим, если он приходит на рабочее место с опо­зданием более 5 мин. Исследование проводили в течение одной недели- 6 рабочих дней. Данные занесены в таблицу 7.3.

 

Таблица 7.3.

Отдел	Пон	Втор	Сред	Четв	Пятн	Суб	сумма
	кредитный
	финансовый
	аналитический
	производственный
	сумма

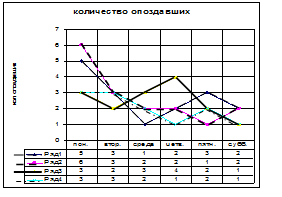
Рисунок 7.3.

 

Из диаграммы 7.3. хорошо видно, что максимальное количество опо­здавших бывает в понедельник. Большое колебание числа опоздавших в отделе 3. Мало опоздавший и число постоянно небольшое в отделе 4. Много опаздывают в отделах 1 и 2 (по 16 случаев). Из анализа графика и таблицы видно, что больше всего опаздывают в понедельник (17) и меньше всего в субботу (6) случаев.

Временные диаграммы хорошо применять для определения законо­мерностей развития технологического процесса за определенный доста­точно большой отрезок времени.

Пример. На рисунке 7.4. показан график наблюдения процесса точения раз­мера на металло­режущем станке. Поставлена задача точить размер, номинальный раз­мер 60 мм с допуском + 0,1 мм. Наблюдения прово­дились длительное время, замер заготовки производился каждые 20 минут. На графике хорошо видно, что на участке 1-5 про­цесс был ста­билен – все размеры группируются вокруг номинала 60 мм, равно­мерно уходя в плюс и минус. В районе 7 замера про­изошел выброс – резкий вы­ход размера в минус 59,82 мм и за пределы допуска. В это время в про­цесс вмешался случайный непредвиденный фактор, который значи­тельно отклонил результат ра­боты от запланированного. После этого процесс снова вернулся практически к но­миналу - 8 замер. После этого в про­цессе появился доминирующий незапланиро­ванный фактор, кото­рый сис­темно и постоянно стал увеличивать размер точения до 13 за­мера, практиче­ски выведя размер за пределы верхнего допуска. На 14 за­мере размер снова вернули к номиналу. Скорее всего была произведена подна­ладка станка. Но с этого замера размер снова постоянно и сис­темно начал увели­чиваться и дви­гаться в сторону верхнего допуска, замеры 15- 19. Скорее всего незапланирован­ным факто­ром вызывающим это отклоне­ние является ускоренный износ резца, вследст­вие неправильно уста­нов­ленных режимов обработки. На замере 20 произошел выброс вверх, размер резко вышел за пределы допуска 60,2 мм.

На участке с 22 за­мера по 30 про­исходит резкая дестабилизация процесса, причем эта дестабили­за­ция вызвана влиянием сильных случайных факторов – размер резко прыгает из плюса в минус, имеется выброс вверх - 60,22 мм. Причи­ной такой сильной дестабилизации процесса скорее всего яв­ляется значительная разладка станка, потеря им жестко­сти. На 31 замере произошел сдвиг вниз, в процессе появился сильный системный фактор.

С 39 за­мера произведена подналадка станка, что сразу стабилизи­ровало процесс. В дальнейшем процесс идет стабильно.

На графике могут быть выявлены следующие участки:

1). Выбросы - это результат, который резко отличается от всех дру­гих и вы­хо­дит на пределы нормальной вариации. Причиной выброса является какой либо сильный случайный фактор, оказавший влияние на процесс в данный момент, это влияние обычно краткосрочное. При по­явлении выброса доста­точно легко выявить этот случайный фактор и принять меры, чтобы в даль­нейшем он не влиял на про­цесс.

2). Тренды – это устойчивое постепенное изменение результата процесса в сто­рону увеличения или уменьшения. Появление тренда вы­звано наличием систем­ного постоянного фактора, который изменя­ется по определенному за­кону, обычно линейному.

3). Серии – это последовательность ряда результатов, в которых каждое оче­редное чуть больше или меньше предыдущего.

4). Сдвиги – это внезапные скачки вверх или вниз результатов, вы­званное ка­ким либо сильным постоянным фактором, который не по­зво­лит результатам вер­нуться к исходным значениям.

г) Диаграммы разброса. Диаграммы разброса представляют из себя графики, которые позво­ляют выявить корреляцию (статистическую зависимость) между различ­ными фак­торами, влияющими на показатели качества. Диаграмма стро­ится по двум координатным осям, по оси абс­цисс откладывается значе­ние изменяемого параметра, а на оси ординат откладывается получаемое на практике значение исследуе­мого параметра, которое мы имеем в момент использо­вание изменяемого па­раметра, на пересече­нии этих значений ставим точку. Собрав достаточно большое количе­ство таких точек, мы можем делать анализ и вывод. Ионгда такой график называется точечным.

Пример. Ученые исследуют влияние температуры на сохранность продукта. Берется входной фактор –температура воздуха в холодильнике и выходной параметр – количество часов сохранения продукта, например пиво. Пиво считается испорченным, если в нем количество определенной кислоты превышает допустимый уровень. Провели серию экспериментов. Закладывали в холодильник партию свежего пива, устанавливали определенную температуру и затем определяли, через какое время пиво становилось испорченным.

 

Таблица 7.4.

Температура, С0									-2
Время, час	12,2		26,5		38,8	45,5	64,4

Рисунок 7.5.

 

На рисунке 7.5. хорошо видна зависимость (корреляция) между температурой и временем сохранности, чем меньше температура, тем больше время сохранности (обратная корреляция).

 

Основы статистических методов анализа и расчета

 

В результате непосредственных наблюдений, измерений или реги­страции фактов получается множество данных, которые обра­зуют стати­стическую сово­купность и нуждаются в обработке, вклю­чающей систе­матизацию и клас­сификацию, расчет параметров, ха­рактеризующих эту совокупность, со­став­ление таблиц, графиков, иллюстрирующих процесс.

Реально на практике бывает достаточно трудно изучить все объекты статистической совокупности, поэтому для оценки всей совокупности используют данные выборки. Что такое выборка? Выборка – это часть совокупности, которая достаточно полно может характеризовать всю совокупность по интересующему нас параметру. Основное требование к выборке – она должна максимально отражать изучаемые параметры всей совокупности. Отсюда выборка должна браться из разных мест совокупности, желательно хаотично, иметь достаточно большой объем. Например, на элеватор приходит грузовик с зерном, в грузовике 15 тонн зерна. Необходимо измерить влажность зерна. Достаточно трудно измерить влажность всего зерна, но можно взять по 100 грамм зерна в 6 местах кузова зерна, и имея 600 грамм зерна произвести измерение влажности этих граммов. Результат этого измерения с некоторой погрешностью можно считать влажностью всего зерна в кузове.

В теории статистики между характеристиками совокупности и выборки есть разница, но с увеличением объема выборки она уменьшается. Для практических расчетов с достаточной долей точности можно эту разницу не учитывать.

Как уже указывалось в разделе 5 основной характеристикой средства измерения является его погрешность. Погрешности бывают систематические и случайные. Для объективного получения величины погрешности и ее влияния на метрологический параметр объекта необходимо применять статистические методы.

В результате непосредственных наблюдений, измерений или регистрации фактов получается множество данных, которые обра­зуют статистическую сово­купность и нуждаются в обработке, вклю­чающей систематизацию и клас­сификацию, расчет параметров, ха­рактеризующих эту совокупность, со­став­ление таблиц, графиков, иллюстрирующих процесс.

Наиболее полную характеристику статистической совокупности дает функция распределения вероятностей случайной величины. Однако на прак­тике используют ограниченное количество числовых характеристик, называе­мых параметрами распределения. Эти пара­метры можно разделить на три класса, которые характеризуют: 1) центр группирования; 2) величину рассея­ния степень вариации; 3) форму распределения вероятностей.

Центр группирования. Одной из основных характеристик ста­тистической совокупности, дающей представление о том, вокруг ка­кого центра группируются все значения, является среднее арифме­тическое. Оно определяется из выражения:

(7.1.)

 

где Хi – измеренный параметр i – члена совокупности, n – ко­личество членов совокупности.

Величина рассеяния. Статические совокупности могут иметь близкие или даже одинаковые значения центра группирования, но отдельные значения ве­личин в них могут существенно отличаться, вследствие того, что разброс зна­чений относительно центра бывает разный. Самой элементарной характери­стикой рассеяния является вариационный размах R, определяемый по формуле

 

R=Xmax - Xmin (7.2.)

 

где Xmax, Xmin – максимальное и минимальное значения ста­тистической совокупности.

Вариационный размах не всегда характерен, так как учитывает только крайние значения, которые могут сильно отличаться от всех других значений. Более точно рассеяние определяется с помощью показателей, учитывающих отклонение всех значений от среднего арифметического. Основным из этих показателей является среднее квадратичное отклонение результата наблюдений, которое еще называется стандартным отклонением. Оно определяе­тся по формуле

(7.3.)

 

Это отклонение является наиболее распространенным и обще­принятым показателем вариации. Величина под корнем, то есть s ², называется диспер­сией. Дисперсия имеет самостоятельное значение во многих задачах математической статистики и относится к числу важнейших показателей ва­риации.

Показателем отклонения значения самого среднего арифметического яв­ляется среднее квадратическое отклонение среднего значения S, которое еще называют среднее квадратическое отклонение результата измерения или стандартной ошибкой.

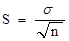(7.4.)

 

Форма распределения вероятности. Важнейший параметр статистической совокупности. Форма распределения зависит от характера и особенностей выполнения процесса, при котором получается совокупность. В производственном процессе достаточно часто проявляется нормальное распределение. Однако нормаль­ное распре­де­ление не является единственно возмож­ным. В зависимости от фи­зи­ческой при­роды случайных величин, некоторые из них на практике могут иметь рас­пределение другого вида, напри­мер, лога­рифмиче­ское, экс­поненци­альное, Вейбулла, Симпсона, Ре­лея, равной веро­ятности, треугольное и т.д.

Нормальное распределение проявляется при выполнении следующего условия- необходимо получить заранее заданный результат метрологического процесса, например размер диаметра вала при точении на токарном станке. Для достижения запланированного результата необходимо выполнение заданных технологических условий работы: оборудование, инструмент, режимы резания, квалификация работника, среда, заготовка и т.д. Это объективные условия. Также требуется выполнение субъективного условия: выполнение работником заданных правил, которые могут нарушаться осознано или случайно. Существует уравнение достижения цели:

(7.5.)

 

Y- параметр, который необходимо получить, в нашем случае размер диаметра вала, X – необходимые технологические условия для получения параметра Y, - случайные параметры, которые влияют на величину параметра Y, это может быть разная твердость заготовки, сбой в механике станка, не внимательность работника и множество других факторов, которые трудно или невозможно заранее предсказать.

Но может быть другая технологическая ситуация. Завод производит сборку автомобилей. Двигатели для автомобиля поставляют 3 разных завода А, Б и В, причем количество поставляемых двигателей у каждого завода одинаковое. Ресурс двигателя А= 100 тыс. часов, двигателя Б= 105 тыс. часов, двигателя В= 96 тыс. часов. Все эти параметры соответствуют нормативным требованиям. После установки двигателей, автомобили продаются потребителям. Если произвести замер функционального метрологического параметра автомобиля, зависящего от качества изготовления двигателей, например износ поршневых колец, то будет ясно видна закономерность разделения автомобилей на 3 равные группы. Ясно, что у автомобилей с двигателями В износ будет больше, а двигателей Б износ будет меньше. В данном случае имеем распределение с равной вероятность получения трех вариантов в статистической совокупности. Вероятность установки каждого варианта двигателя составляет 1/3 от всего количества изготовленных автомобилей.

Для характеристики формы распреде­ления обычно используют ту математическую модель, ко­торая наилучшим об­разом приближает к виду кривой распределения вероятностей, полученной при анализе экспериментально получен­ных данных.

 

123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: