Определение стабильности по характеру графика наблюдений параметра по времени

Достаточно хорошим инструментом определения стабильности могут быть временная диаграмма. Этот графический документ показывает изменение исследуемого параметра по времени. Например, в цехе идет производство молока, имеется нормативный показатель качества – жирность молока должна быть 3,2%. Данный показатель обеспечивается наличием 3,2 г жира на 0,1 литр продукции. Для контроля процесса технолог ведет временную диаграмму контроля. В каждой партии продукции, которая производится с интервалом в 1 час, берется проба в 5 местах по 0,1 литру, каждом литре определяется масса жира, которая должна в идеале равна 3,2 г. Затем определяется среднее арифметическое, которое и определяет реальный показатель всей партии. В таблице 7.14. показаны данные замеров, а на рисунке 7.9. показан график. Иногда на графике устанавливают верхнее и нижнее предельное значение нормативного параметра, которые определяют допустимый коридор колебания параметра.

 

Таблица 7.14 – Данные замеров жирности молока

№
замер	3,2	3,22	3,24	3,19	3,21	3,18	3,2	3,2	3,24	3,21	3,19	3,21

 

Рисунок 7.9. – График показателя жирности молока

 

По характеру получаемого графика, мы можем делать выводы о процессе. Для принятия обоснованного решения, что процесс стал нестабилен и его необходимо остановить, существует четыре правила:

1. Пять точек подряд находятся с одной стороны от среднего значения. Явная тенденция движения графика к границе зоны допуска, появился системный фактор (Рисунок 7.10.).

Рисунок 7.10. – График 5 точек

 

2. Шесть точек подряд графика все либо повышают, либо понижают значение параметра. Также появился системный фактор (Рисунок 7.11.)..

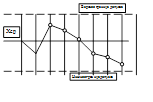
Рисунок 7.11- График 6 точек

 

3. Четырнадцать точек графика попеременно оказываются то выше, то ниже среднего значения. Несогласованность в проведении процесса, существуют два фактора, действующих резко в разных направлениях (Рисунок 7.12.).

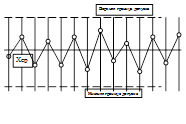
Рисунок 7.12 – График 14 точек

 

4. Пятнадцать точек подряд находятся в зоне всего одной стандартной ошибки от среднего значения. Процесс стал более стабилен, чем требуется по нормативам. Требуется разобраться, почему так произошло (Рисунок 7.13.)

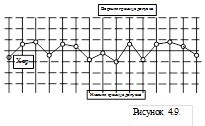
Рисунок 7.13. – График 15 точек

 

4.Корреляционный анализ

 

 

Статистические методы прогнозирования

Статистические методы прослеживают значение метрологического параметра во времени. Исследуя эти значения можно проследить общую тенденцию развития процесса и достаточно точно прогнозировать пути движения процесса в будущем. Статистические методы являются мощным инструментом проведения прогнозного анализа. Для проведения такого прогноза очень важно от каких факторов и как зависит значение контролируемого технологического параметра.

Корреляционный анализ

В производственном процессе очень часто необходимо опреде­лить зависимость между разными факторами. Причем необходимо отметить, что если эта связь и существует, ее трудно выявить, так как на процесс влияют и другие, неучтенные нами факторы. В произ­водственной прак­тике очень часто связь между процессами имеет стохастический (слу­чайный или если выразиться более точно не выявленный) характер, а не функциональный (детерминированный). Стати­стическая стохастическая зависимость называется корреляци­онной. Эта зависимость возникает тогда, когда один из признаков зависит не только от одного определенного нами фактора, но и от ряда других случайных неучтенных факторов. Виды корреляционных связей могут быть раз­ными, это линейная и нелинейная, положитель­ная и отрицательная. С целью выявления характеристики корреляци­онной зависимости приме­няют корреляционный анализ. Термин «корреляция» был введен в тео­рию статистики английским ученым Ф. Гальтоном.

Корреляционный анализ представляет собой совокупность ос­нован­ных на ма­тематической теории корреляции мето­дов обнаруже­ния корре­ляционной зависи­мости между двумя случайными призна­ками или фак­торами. При этом две слу­чайные величины считаются корреляционно связанными, если матема­тическое ожидание одной из них меняется в за­ви­симости от изменения дру­гой.

Корреляционный анализ обычно применяется для оценки зависи­мо­сти качества конечной продукции от определен­ных свойств сырья или исходных ма­териалов либо режимов работы. Этот вид анализа требует от исполнителя тща­тельности, так как при изме­нении условий экспери­мента вместе с изме­нением исследуемого по­казателя качества сы­рья или материала могут изме­няться и другие показатели их каче­ства. Если не учитывать эти из­менения, то могут возникнуть значи­тельные ошибки в оценке оконча­тельного качества.

Пример. В цехе ведется обработка изделия на токарном станке. Имеется вход­ной параметр процесса точения – момент затяжки болтов резцедержателя станка, который определяет жесткость си­стемы резания металла. Технолог хочет определить имеется ли зави­симость между этим входным параметром и выходными параметрами процесса, влияющими на качество, а именно точ­ность обработки, силой резания, временем стойкости резца (время между двумя заточ­ками) и расходом электроэнергии. В течение некоторого времени проводились опытные обработки на станке. Вводилось некоторое значение входного параметра и определялись значения выходных параметров. Значения заносились в таблицу 7.20.

 

Таблица 7.20 – Данные замера

	Входной па­раметр	Выходные параметры
	Момент за­тяжки резца, Нм	% год­ных из­де­лий	Сила резания, КН	Стой­кость резца, мин	Расход э/энергии, кВт/час
			15,5		2,5
		96,5
			14,1		3,5
			12,2		2,9
			8,5		3,4
		98,5	9,6		4,1
			9,1		2,8

Рисунок 7.15 – График % годных

Рисунок 7.16- - График силы резания

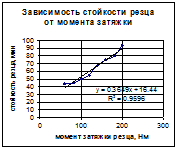
Рисунок 7.17 – График стойкости

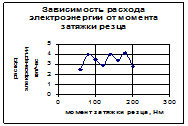
Рисунок 7.18 – График расхода энергии

 

Чтобы легче было видеть корреляцию необходимо построить график, лучше всего диаграмму разброса. Диаграммы разброса удобно строить с по­мощью пакета EXCEL. В мастере построения диаграмм имеется тип графика «точечный». Это и есть диаграмма разброса. Более того пакет позволяет, кроме нанесения точек, по­строить линию тренда. Тренд- это график какой либо функции, макси­мально близко описывающей положение точек эмпири­ческих данных, кото­рую можно выразить аналитически в виде формулы. С помощью тренда мы можем видеть закономерность развития про­цесса в бу­дущем, а с помощью аналитического выражения произво­дить прогнозные расчеты. EXCEL по­зволяет сразу получить аналити­ческую формулу макси­мально, описывающую траекторию тренда и коэффициент де­терминации. Для получения линии тренда необхо­димо установить курсор на любую точку на графике и нажать правую кнопку «мыши», появится афиша, в которой есть фраза «добавить линию тренда», с учетом расположения точек необходимо выбрать тип зависимости и значит вид графика. Это может быть зависимость линейная (Y=ax+b), логарифмическая (Y=a Ln(x)+b), полиноми­нальная (Y= ax² + cx + b), степенная (Y = ax^c), экспоненциальная (Y =ae^cx), линейная фильтрация. Для получения коэффициента детерми­нации (величина досто­верности аппроксимации) в разделе «пара­метры» необходимо поставить метки в соответствующие квадратики.

Одной из основных задач анализа является выявление входных факторов Х, максимально влияющих на выходной параметр Y. Наиболее часто встреча­ется линейная корреляции, то есть определе­ние линейной зависимости между двумя факторами- входным и выходным. На диаграммах 7.16 и 7.17 видны линейные обратно пропорциональная (отрицательная) зависимость между факторами и прямо пропорциональная (положительная) зависимость между факторами. Корреляция позволяет количественно выразить эту зави­симость. Количественно оценить, насколько линейна зависимость между двумя пере­менными, позволяет коэффициент корреляции r.

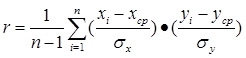(7.13.)

Формулу расчета коэффициента корреляции разработал К.Пирсон, ученик Ф.Гальтона. Расчетный коэффициент корреляции всегда находится в пределах от -1 до +1. Знак коэффициента говорит о зависимости. Если знак (+) зависи­мость положительная при возрастании Х возрастает и Y. Если знак (-) зависи­мость отрицательная, при возрастании Х, значение Y уменьшается. При­ближение коэффициента к /1/ показывает величину приближения зависимо­сти к линейной, если коэффициент равен 1, независимо от знака, линейная зависимость полная.

При пользовании пакетом EXCEL и построении точечных диаграмм при­ближение корреляции к линейности или зависимости другого вида можно быстро определять по коэффициенту детерминации R² (величина достоверно­сти аппроксимации). В дальнейшем для определения уровня приближенности корреляции к линейности или кривой лучше пользоваться коэффициентом детерминации.

Коэффициент детерминации R² – это отношение регрессивной квадра­тич­ной ошибки (РКО) к полной квадратичной ошибке (ПКО).

(7.14.)

Где Y_Тi – теоретическое значение выходного параметра (по формуле), Y_срф - средне арифметическое значение реального показателя выходного параметра, Y _рi – реальное (опытное) значение выходного параметра.

Определим коэффициент R² для нашего примера – зависимости - момент затяжки и стойкость резца. На рисунке 7.19. EXCEL определил формулу аналитической зависимости как 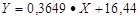и R² = 0.9596. Проверим этот результат.

Как видно результат практически совпал (Таблица 7.21.)

 

Таблица 7.21 - Результаты расчета

Х	Yр	(Yр-Yсрф)2	YТ	(YТ-Yсрф)2
		395,015625	38,334	652,342681
		356,265625	45,632	332,807049
		192,515625	52,93	119,793025
		78,765625	60,228	13,300609
		17,015625	67,526	13,329801
		123,765625	74,824	119,880601
		260,015625	82,122	332,953009
		907,515625	89,42	652,547025
		ПКО		РКО
сумма		2330,875		2236,9538
Yсрф	63,875
	R2	0,959705604

 

Коэффициент R² показывает, какая часть полной наблюдаемой вариации соответствует нашему аналитическому выражению (формуле). Чем ближе коэффициент к 1, тем более достоверна формула, при R² = 1, формула пол­ностью описывает закономерность появления данных, все точки находятся на линии аналитического графика (тренда). Если в случае построения линейной зависимости R² = 1, линейная зависимость полная. Характер зависимости можно определить по графику. Угол наклона прямой на графике показывает силу зависимости. Чем более круто наклонена прямая тем, больше зависимость.

Корреляция может иметь и не линейный характер. На диаграмме – рисунке 7.15. корреляция не линейная, причем график имеет экстремальную точку- пик. На диаграмме-рисунке 7.18. корреляции нет, точки расставлены без всякой системы, то есть зависимости этих двух факторов нет.

В примере с моментом затяжки резца, мы определили три фактора влияющие на качество продукции, видим общую закономерность влияния, но для определения точной функциональной зависимости необходимо получить аналитическую форму этой зависимости(формулу функции, максимально полно от­ражающей данную зависимость. Для этого необходимо провести регрессионный анализ. Данный анализ подробно рассмотрен в разделе……

 

 

Подготовка эксперимента

Проведение эксперимента

Планирование эксперимента

 

ТЕОРИЯ ЭКСПЕРИМЕНТА

 

Эксперимент позволяет практически определить причинно- следственную связь между явлениями. Выводы можно делать после достаточно длительного и объективного наблюдения. Следует помнить, что если в процессе поя­вился какой либо фактор и вслед за этим произошло изменение выходной величины, это не значит, что этот фактор является причиной появления изменения исследуемого параметра. Это может быть только совпадением. Также в реальности на процесс влияет множество факторов, явных (хорошо заметных) и неявных (скрытых). Задача определения количественного влияния факторов на процесс сложнейшая за­дача. Здесь следует применить методы планирования эксперимента. То есть выявить факторы, установить их значения, провести эксперимент и установить их влияние на выходной параметр (отклик).

Любой процесс, протекающий в реальности, и в частности в производстве, сфере услуг происходит по какой либо зависимости. Задачей исследователя обычно является определение и нахождение этой зависимости, чтобы впоследствии можно было достаточно точно прогнозировать результаты процесса, который только должен произойти. По своему происхождению и виду зависимости могут быть теоретическими и статистическими. Теоретические зависимости это зависимости, которые могут быть описаны с высокой точностью математическими формулами, например площадь прямоугольника может легко быть описана одной формулой S= A B, в которой точно отражена зависимость площади от длин сторон прямоугольника A и B. Но часто в жизни характер развития процесса часто зависит от множества факторов, которые воздействуют на процесс по разному, поэтому такой процесс практически невозможно точно описать математическими формулами. В этом случае зависимости по которым протекает процесс называют статистическими. Эту зависимость можно определить, только проведя эксперимент, то есть практически воспроизведя изучаемый процесс и непосредственно проведя во время процесса замер параметров, определяющих зависимости по которым происходит процесс.

Эксперимент может быть разных видов (рисунок 8.1.) Прежде всего эксперимент может быть активным или пассивным. Активным экспериментом называется такой эксперимент, в ходе которого исследователь сам назначает режим работы исследуемого объекта. Пассивный эксперимент, или наблюдение, ведется в ходе обычного функционирования изучаемого объекта или процесса. В свою очередь активный эксперимент может быть натурным или модельным. Натурный эксперимент проводят непосредственно на исследуемом объекте, он наиболее достоверен, но такое исследование не всегда можно провести на практике. Поэтому приходится иногда проводить эксперимент на моделях, физических или математических. Суть любого эксперимента состоит в том, что необходимо что-то задать, а затем после эксперимента что-то замерить.

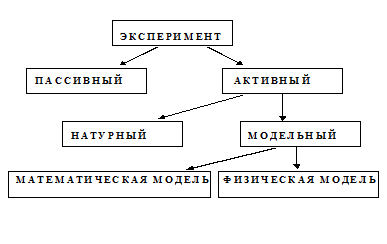
Рисунок 8.1 – Виды эксперимента

 

В ходе эксперимента определятся входные параметры Х (факторы) и получаемые значения, выходные параметры Y (отклики).

Целью экспериментов является нахождение функций отклика. Для достижения этой цели необходимо выполнить следующие работы: планирование и проведение эксперимента, получение экспериментальных данных, обработка результатов эксперимента. Проведение эксперимента и по­лучение данных составляют главную и самую трудоемкую часть экспери­мента. Проведение каждого конкретного эксперимента зависит от процесса или объекта над которым проводится эксперимент. эта часть экс­перимента обычно всегда индивидуальна и здесь рассматриваться не будет. Поэтому рас­смотрим общие положения, присущие практически всем экспе­риментам: пла­нирование эксперимента и обработка полученных данных.

 

Планирование эксперимента

Вопросом разработки планов проведения экспериментов занимается специальная наука, которая называется – теория планирования эксперимента. Рассмотрим лишь отдельные наиболее общие и важные положения этой теории, по которым можно определить зависимости между параметрами. Все параметры объекта эксперимента прежде всего необходимо, исходя из возможностей эксперимента и его физического содержания, разделить на факторы и отклики. В эксперименте каждому фактору необходимо придавать различные значения. Поэтому при планировании эксперимента возникают три основные задачи: 1. Сколько проводить экспериментов, 2. Какие значения придавать факторам, 3. В каком сочетании различным факторам придавать различные значения.

1. Сколько проводить экспериментов. Цель эксперимента – получить функцию отклика. Следовательно, необходимо знать сколько провести экспериментов, чтобы с достаточной заданной точностью получить функцию отклика. Для ответа на этот вопрос допустим, что в результате эксперимента состоящего из N опытов, в котором один фактор х₁ и один отклик у₁, получены значения, показанные, например на графике рисунок 8.2.

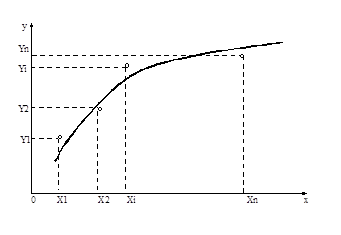
Рисунок 8.2 – График эксперимента

 

Для получения аналитической зависимости надо, чтобы ее график был как можно ближе к экспериментальным точкам на графике. Такую функцию отклика называют аппроксимирующей и обозначают y = f (x). Следует иметь в виду, что обычно видом аппроксимирующей функции задаются. В результате обработки экспериментальных данных находят коэффициенты аппроксимируемой функции и выражают ее аналитически в виде уравнения.

Если фактор один то функция будет линейной, и уравнение такой функции выглядит следующим образом:

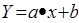
Это функция одного фактора и одного отклика, график такой функции всегда расположен на плоскости.

Если факторов два то функция отклика будет располагаться уже в трехмерном пространстве, и ее график будет являться поверхностью. В общем виде функция отклика будет иметь вид:

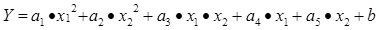
В данном случае число коэффициентов, которое необходимо определить в результате эксперимента, равно 6. В общем случае поверхность отклика второго порядка для р факторов имеет вид

(8.1.)

Число коэффициентов в такой зависимости

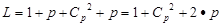
Где C²_p - число сочетаний из р факторов по два, что равно числу парных произведений. Оно равно

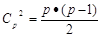
Окончательно после несложных преобразований нетрудно найти, что число коэффициентов в многочлене второго порядка при различном числе факторов равно

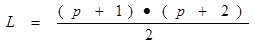(8.2.)

Значения L для некоторых значений р приведены в таблице 8.1.

 

Таблица 8.1.

р
L

 

Для того чтобы найти неизвестные, число уравнений должно быть равно числу неизвестных. Чтобы найти L коэффициентов, надо провести N= L экспериментов. Но это в теории. В жизни на результат эксперимента влияют всевозможные случайные факторы, следовательно, чем больше будет экспериментов тем более точный результат получит исследователь, но в любом случае N ³L. Таким образом определяется минимально возможное количество экспериментов.

2. Какие значения придавать факторам? Для каждой переменной должны быть заданы граничные условия a_i £ x_i £ b_i. Величина х_i измеряется в некоторых единицах определенной размерности. Такие значения х_i будем называть натуральными. Для универсальности описания в планировании эксперимента имеют дело с относительными переменными y_i. Переход от натуральных переменных x_i к относительным y_i производится по зависимости

(8.3.)

где x_цi= (a_i+b_i)/2 - центральное значение, то есть значение х_i в середине интервала, D x_i= (b_i-a_i)/2 - половина интервала. Так, если параметр задан в граничных условиях 100 £ х_i £200.

X_цi = (100 + 200)/2 = 150

Dx_i= (200 – 100) /2 = 50

Относительная переменная

g_i = (x_i – 150)/50

При х_i = a_i, то есть на нижней границе

 

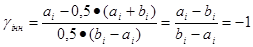
аналогично на верхней границе при х_i = b_ig_iвг = 1 и в центре интервала g_iц = 0.

Таким образом, с помощью выражения (8.3.), мы перешли от натуральной переменной х_i, которая может принимать значения в интервале a_i£ x_i £ b_i, к относительной переменной g_i, принимающей значения -1 £ g_i £ 1. Из выражения (8.3.) следует и обратный переход: х_i = x_iц + Dх_ig_i. В дальнейшем в эксперименте факторами являются величины g_i, которые в интервале -1 £ g_i £ 1.

С точки зрения значений, которые необходимо придавать каждому фактору, эксперименты могут быть двух -,трех- и многоуровневыми. В двухуровневом эксперименте факторам последовательно придаются два значения: g_i = 1; g_i = -1. Двухуровневый эксперимент можно проводить в том случае, когда принимают, что функция отклика представляет собой линейную зависимость. Трехуровневый эксперимент дает все необходимые данные для получения функции отклика второго порядка. В таком эксперименте каждому фактору придается три значения: g_i = 1; g_i = 0; g_i = -1.

Многоуровневый эксперимент применяют. когда с помощью отклика второго порядка экспериментальные данные аппроксимировать не удается.

3. В каком сочетании следует придавать различным факторам различные значения? Двухуровневый эксперимент. Все возможные сочетания значений факторов в двухуровневом эксперименте показаны для двух факторов (р = 2) в таблице 8.2. и для трех факторов в таблице 7.3.

Таблица 8.2- N²пфэ = 2²= 4

Номер опыта	Х1	Х2
		-1
	-1
	-1	-1

 

Таблица 8.3- N³пфэ = 2³ = 8

Номер опыта	Х1	Х2	Х3
			-1
		-1
		-1	-1
	-1
	-1		-1
	-1	-1
	-1	-1	-1

 

Таблицы показывают закономерность формирования сочетаний разных факторов. Такой эксперимент, в котором опыты проводят при всех возможных сочетаниях факторов, называют полным факторным экспериментом (ПФЭ). Сочетание факторов в трехуровневом ПФЭ приведено для двух факторов в таблице 8.4. и для трех факторов в таблице 8.5.

 

Таблица 8.4- N³пфэ = 3² = 9

номер опыта	Х1	Х2
		-1
		-1
	-1
	-1
	-1	-1

 

Таблица 8.5- N³пфэ = 3³ = 27

Номер опыта	Х1	Х2	Х3	Номер опыта	Х1	Х2	Х3
						-1
						-1	-1
			-1
				…	…	…	…
			-1		-1	-1
		-1			-1	-1	-1

 

 

Аналогично можно составить последовательность проведения опытов для любого числа уровней S и факторов р. нетрудно убедиться, что число опытов в ПФЭ находится по формуле:

N_пфэ = S^p,

 

Где S – число уровней, p – число факторов. Значения Nпфэ для некоторых S и p приведены в таблице 8.6.

 

Таблица 8.6.

S	р

 

Сравним число коэффициентов L, которое необходимо определить в ходе эксперимента (таблица 8.1.) и величину Nпфэ (таблица 8.6.). Для удобства сравнения эти величины сведем в таблицу 8.7.

 

Таблица 8.7.

р
N2пфэ=2р
N3пфэ=3р
L

 

Двухуровневый ПФЭ применим только в случае линейной зависимости между откликами и факторами. Что касается трехуровневого ПФЭ, как видно из таблицы, при нем число проводимых опытов существенно выше числа искомых коэффициентов. Проведение каждого опыта трудоемкая работа, поэтому естественно было бы желательно уменьшить их число до минимального допустимого значения.

Рассмотрим два пути сокращения числа опытов.

1). Проведение дробного факторного эксперимента. В этом случае из всех опытов, необходимых при ПФЭ, некоторые сочетания исключаются и опыты при этих сочетаниях не производятся. Есть разные правила исключения некоторых сочетаний. Они рассматриваются в специальной литературе и здесь рассматриваться не будут. Отметим лишь, что опыты, в которых все факторы находятся на одном уровне (1, 0, -1), исключать не следует.

2). Составление композиционных планов. Здесь за основу принимают двухуровневый ПФЭ и к нему добавляют эксперименты, проводимые на других уровнях: как в центре, так и при различных значениях + a, где a > 1. поскольку в нашем случае /a/ > 1 выходит за заданные для факторов граничные условия, мы такие варианты рассматривать не будем. Рассмотрим только один вариант составления композиционных планов. В нем за основу принят двухуровневый ПФЭ и к нему добавляют опыты, которые проводят только в центре, то есть при gi = 0. Есть различные рекомендации по числу дополнительных опытов. Одна из них заключается в том, что в центре проводится

 

 

Опытов, то есть столько же, сколько проводится на каждом уровне, верхнем и нижнем. Тогда общее число опытов при таком композиционном плане

 

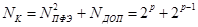
Значения Nдоп и Nк для различных р приведены в таблице 8.8., из которой видно, что L < Nк < N³пфэ.

Таблица 8.8.

р
N2пфэ = 2р
Nдоп = 2 р-1
L
Nк
N3пфэ = 3р

Поясним это на примере для случая р= 3. При р = 3 число опытов в композиционном плане

 

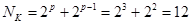
При этом 6< 12 < 27, то есть композиционный план, состоящий из Nк = 12 опытов, дает возможность определить необходимые 6 коэффициентов, и в то же время по числу опытов он меньше, чем N ³пфэ = 27.

Пример композиционного плана для трех факторов (р = 3) приведен в таблице 8.9., из которой видно, что первые 8 опытов представляют собой план при двухуровневом ПФЭ, а последние 4 опыта проводятся в центре плана.

 

Таблица 8.9.

Номер опыта	Х1	Х2	Х3	Номер опыта	Х1	Х2	Х3
					-1	-1
			-1		-1	-1	-1
		-1
		-1	-1
	-1
	-1		-1

 

После проведения эксперимента необходимо провести обработку полученных данных. Обработка производится различными методами в зависимости от цели эксперимента. Наиболее часто встречающаяся в научной практике цель – нахождение функции отклика, то есть аналитическое выражение эмпирических данных эксперимента. В этом случае чаще всего применяется метод наименьших квадратов.

Представим, что проведено N опытов и получены результаты, сведенные в таблицу. Необходимо найти аналитическую зависимость, описывающую функцию отклика y = f (x). При этом надо, с одной стороны, точно отразить общую тенденцию зависимости отклика от факторов, а с другой стороны – не учитывать случайные отклонения в отклике, связанные с неизбежными случайными погрешностями при проведении опыта. Нахождение такой зависимости включает два этапа: 1) выбор аналитической зависимости y = f (x), 2) определение коэффициентов в зависимости от выбранного вида.

Выбор вида аналитической зависимости производят по виду экспериментальных данных. В настоящее время разработано множество программных продуктов для компьютера, которые позволяют достаточно быстро решать подобные задачи. Например EXCEL, примеры получения аналитических зависимостей показаны ниже в разделе 8.3. на примере построения диаграммы разброса (точечной диаграммы). При работе с такими программами достаточно ввести порядок многочлена, которым необходимо аппроксимировать наши экспериментальные данные, сами экспериментальные данные, и компьютер выдаст уравнение функции отклика. Такие функции отклика являются уравнениями регрессии, которые могут быть линейными и нелинейными, однофакторными и многофакторными. Точность подбора функции отклика оценивают разными методами, которые описаны в специальной литературе.

Цель эксперимента.

1. Понять какие входные факторы Х существенно влияют на выходной параметр Y, а какие Х влияют не существенно.

2. Сформулировать и выразить количественно математическую зависимость между значениями Х и выходным параметром Y.

3. Статистически подтвердить, что процессе произошли изменения и определить в какую сторону, улучшения или ухудшения.

4. Определить, какие значения Х в комбинации друг с другом приведут к максимальному улучшению параметра Y.

Сила и значение эксперимента в том, что он позволяет точно сформулировать, выразить и проверить зависимость Y= f(X). Знание уравнения Y= f(X) открывает нам окно в будущее, мы можем достаточно точно прогнозировать результаты будущего процесса при установке соответствующих значений входных факторов Х.

В результате проведения эксперимента мы получаем уравнение Y= f(X), в котором указаны критичные (крайние) значения входных факторов Х и количественная оценка их влияния на выходной результат Y. Например, мы проводим маркетинговую компанию, работаем с разными видами рекламы. Выходной фактор этого проекта увеличение положительной осведомленности покупателей о нашем товаре. В результате мы можем узнать, какие виды рекламы – радио, телевидение, газеты, журналы, интернет, раздача буклетов на улице и т.д., в каком сочетании (это есть входные параметры Х) больше и лучше влияют на конечный результат – выходной фактор.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: