 |
Пример проведения простейшего эксперимента
|
|
|
|
Производится исследование процесса точения изделия вал на токарном станке. Цель процесса изготовление шейки вала в размер 70 мм. Необходимо выяснить, как влияют отдельные входные факторы на точность точения заданного размера. Для простоты выберем три фактора.
1. Фактор Х1. Материал режущей части резца минералокерамика Т12К8 или Т15К6.
2. Фактор Х2.Угол заточки передней поверхности резца 10 или 20.
3. Фактор Х3. Скорость подачи 4,6 мм/мин или 6,2 мм/мин.
Таблица 8.10.
| Фактор | Обозначение | Нижнее значение | Верхнее значение |
| Материал режущ. части | Х1 | Т12К8 (-1) | Т15К6 (+1) |
| Угол заточки, град | Х2 | 10 (-1) | 20 (+1) |
| Скорость подачи, мм/мин | Х3 | 4,6 (-1) | 6,2 (+1) |
Составляем матрицу эксперимента, при этом нижнему значению присваиваем значение -1, а верхнему значению +1.
Таблица 8.11.
| № эксперимента | Значение Х1 | Значение Х2 | Значение Х3 |
| -1 | -1 | -1 | |
| +1 | -1 | -1 | |
| -1 | +1 | -1 | |
| +1 | +1 | -1 | |
| -1 | -1 | +1 | |
| +1 | -1 | +1 | |
| -1 | +1 | +1 | |
| +1 | +1 | +1 |
Производим эксперимент, то есть устанавливаем заданные значения факторов и замеряет отклик, то есть точность изготовления размера 70 мм. В процессе экспериментального точения при заданных значениях факторов точим 5 заготовок и определяем среднее арифметическое значение заданного размера 70 мм.
При проведении эксперимента на его результат могут повлиять скрытые неизвестные нам факторы, а мы по ошибке влияние этих неизвестных факторов будем приписывать заданным факторам. Для максимального исключения таких незапланированных факторов применяется прием хаотичного случайного порядка проведения экспериментов. Необходимо случайным образом определить порядок следования экспериментов. Такой прием называется «рандомизация».
|
|
|
Данные эксперимента заносим в таблицу 8.12.
Таблица 8.12.
| № эксперимента | Порядок выполнения | Значение Х1 | Значение Х2 | Значение Х3 | Значение Yi, размер точения, мм |
| -1 | -1 | -1 | 70,01 | ||
| +1 | -1 | -1 | 70,005 | ||
| -1 | +1 | -1 | 70,012 | ||
| +1 | +1 | -1 | 70,016 | ||
| -1 | -1 | +1 | 69,994 | ||
| +1 | -1 | +1 | 70,008 | ||
| -1 | +1 | +1 | 70,024 | ||
| +1 | +1 | +1 | 70,028 |
Анализируем полученные данные эксперимента. Для этого необходимо определить основной эффект Е каждого фактора Х на результат Y. Основной эффект для факторов определяется как разница между средним значением отклика Y при установке фактора Х на высокое значение +1 и средним значением отклика Y при установке фактора Х на нижнее значение -1.
Фактор Х1 (материал режущей части). Этот фактор качественный, то есть значение нижнее -1 и верхнее +1 взяты условно. В экспериментах 2,4,6 и 8 значение Х1 высокое +1. В экспериментах 1,3,5 и 7 значение Х1 нижнее -1. Основной эффект равен:

Фактор Х2. В данном случае можно применить несколько иную форму записи формула расчета основного эффекта Е.

в данной формуле коэффициент с2i обозначает верхнее или нижнее кодированное значение фактора, то есть +1 или -1.

Фактор Х3. В данном случае расчет производим аналогично.

Запишем общее уравнение для расчета любого эффекта в 2-х факторном эксперименте с помощью относительных установок переменных

где k – количество экспериментальных факторов, i – рассчитываемый основной эффект.
Следующим этапом необходимо определить эффекты взаимодействия факторов, то есть их взаимное действие попарно. Эффект взаимного взаимодействия первого фактора (материал режущей части) и второго фактора (угол заточки) обозначим Е12, эффект взаимодействия второго и третьего Е13, первого и третьего Е13, первого, второго и третьего Е123. Относительные установки для каждого нового случая определяются как умножение относительных установок для одиночного взаимодействия. Например
|
|
|
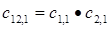 ;
; 
и так далее.
Таблица 8.13.
| № эксперимента | С1 | С2 | С3 | С12 | С13 | С23 | С123 | Значение Yi, размер точения, мм |
| -1 | -1 | -1 | +1 | +1 | +1 | -1 | 70,01 | |
| +1 | -1 | -1 | -1 | -1 | +1 | +1 | 70,005 | |
| -1 | +1 | -1 | -1 | +1 | -1 | +1 | 70,012 | |
| +1 | +1 | -1 | +1 | -1 | -1 | -1 | 70,016 | |
| -1 | -1 | +1 | +1 | -1 | -1 | +1 | 69,994 | |
| +1 | -1 | +1 | -1 | +1 | -1 | -1 | 70,008 | |
| -1 | +1 | +1 | -1 | -1 | +1 | -1 | 70,024 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | 70,028 |
Рассчитаем основной эффект для взаимодействия первого и второго факторов.

Аналогично подсчитываем другие основные эффекты взаимодействия факторов



Следующим этапом необходимо определить значимость воздействия факторов на процесс, велико ли их влияние или оно незначительно и не должно в дальнейшем приниматься во внимание. Если принятые факторы слабо влияют на Y, то рассчитанные основные эффекты и эффекты взаимодействия будут случайными величинами, распределенными вокруг нулевого центрального значения. Напротив если их значения окажутся на значительном расстоянии от нулевого значения их влияние значительно. Для этого построим график на который нанесем все полученные значения эффектов Е и линию нормального распределения. Чем дальше окажется точка эффекта от линии нормального распределения, тем эффект сильнее. Составим таблицу, в которую внесем все эффекты с простановкой ранга, ранг будем присваивать по мере возрастания эффекта.
Таблица 8.14.
| Эффект | Значение Еi | Ранг (i) | Р | Z |
| Е123 | -0,019 | 0,071 | -1,465 | |
| Е12 | -0,001 | 0,214 | -0,792 | |
| Е3 | 0,00275 | 0,357 | -0,366 | |
| Е1 | 0,00425 | 0,5 | ||
| Е2 | 0,01575 | 0,643 | 0,366 | |
| Е13 | 0,019 | 0,786 | 0,792 | |
| Е23 | 0,037 | 0,929 | 1,465 |
Рассчитаем ожидаемую вероятность для каждого ранга. Она обозначается буквой Р и рассчитывается по следующей формуле, k=3 – имеем три фактора.

По специальной таблице определяем значения коээфициента Z, для каждого значения Р имеется свое значение Z, задача упрощается тем, что зависимость Р=f(Z) является линейной и постоянной, имея координаты всего двух точек всегда можно построить график функции Р=f(Z). В принципе значения Z можно и не определять, график Р=f(Z) можно провести как прямую, проходящую через начало координат и максимально приближенную к точкам, определяющим значения эффектов.
|
|
|
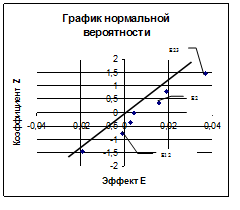
Рисунок 8.3.
При изучении графика (Рисунок 8.3.) видно, что значения эффектов Е12, Е2 и Е23 находятся достаточно далеко от линии графика нормального распределения, но эффект Е12 имеет незначительное значение - 0,001. Следовательно можно считать, что процесс точности максимальное влияние оказывают факторы Е2 и Е23.
В дальнейшем последующие расчеты ведем именно с факторами оказывающими значительный эффект. Для определенных факторов Х2 и Х23 запишем уравнение их влияния на Y причем мы считаем, что зависимость линейная, то есть это должно быть уравнение прямой линии.

Найдем значения коэффициентов β.
β0 – это среднее арифметическое всех значений Yi. β0 = 70,01213 мм.
Значения других коэффициентов β равны половине величины соответствующего эффекта Е.
 ;
; 
Окончательно запишем уравнение влияния значимых факторов на процесс точения и получения заданного размера 70 мм.
 /мм/
/мм/
Имея данное уравнение, мы можем с достаточной точностью прогнозировать результат точения. Для этого в уравнение необходимо подставлять соответствующие значения Х (-1 или +1). Например, мы хотим узнать результат точения при следующих условиях: Х2 – угол заточки резца нижнее значение 10 (-1) и Х3 – скорость подачи верхнее значение 6,2 мм/мин (+1). Подставляем значения в уравнение:
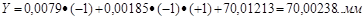
Регрессионный анализ
|
|
|


