Главная | Обратная связь | Поможем написать вашу работу!

Для обработки результатов эксперимента очень удобно применить регрессионный анализ.

Регрессионный анализ заключается в исследовании распределения коэффициентов регрессии, определяющих случайную величину как функцию от нескольких других. Определение неизвестных коэффициентов регрессии и дисперсии осуществляется методом наименьших квадратов. Регрессионный анализ определяет зависимость между случайной и неслучайными величинами. Регрессионный анализ связан с корреляционным. Регрессионный анализ применяется для исследования поведения коэффициентов весомости при комплексной оценке качества продукции.

С помощью регрессионного анализа можно обнаружить и описать связь между выходным фактором и одним или несколькими входными факторами. В регрессионном анализе мы подбираем модели или функции распределения под наблюдаемые данные. В зависимости от данных это могут быть различные функции.

Цель анализа состоит в подборе линии и создании уравнения, которые объясняют и предсказывают развитие процесса в будущем. Существует множество методов получения аналитической формулы, максимально полно описывающей зависимость эмпирических данных, полученных из практических измерений. Это методы - подгонка линии, наименьших квадратов, частных наименьших квадратов, логистическая регрессия, пошаговая регрессия и т.д.

Регрессионный анализ бывает парный и множественный.

Парный анализ. Достаточно прост, здесь необходимо получить аналитическую формулу зависимости одной функции от одного независимого аргумента

В большинстве случаев уравнение, описывающие с максимальной точностью нашу линию тренда, можно записать как полиноминальное уравнение регрессии:

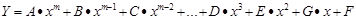(8.4.)

A, B, C, …,D, E, G, F – коэффициенты регрессии. Задача анализа определить эти коэффициенты. Часть коэффициентов может равняться нулю. Если не равны нулю коэффициенты G и F, уравнение регрессии выглядит как, линейное уравнение:

Если не равны нулю коэффициенты E, G и F, уравнение регрессии будет квадратическим и т.д.

и т.д.

Очень эффективно применение специальных компьютерных программ и пакетов. Наиболее доступен пакет EXCEL, а именно построение точечных диаграмм (диаграмм разброса), определение максимально приближенного тренда и определение аналитической формулы тренда. Все расчеты компьютер делает сам. Программа расчета вложена разработчиками EXCEL.

EXCEL позволяет сразу получить аналитическую формулу максимально, описывающую траекторию тренда и коэффициент детерминации. После получения линии тренда, для получения аналитического выражения и коэффициента детерминации в разделе «параметры» необходимо поставить метки в соответствующие квадратики.

Пример. Впроизводится обработка изделия на токарном станке, работа ведется проходным резцом. Технолог хочет узнать характер нагревания резца в зависимости от времени работы. Проведена опытная обработка заготовки. Имеем постоянные режимы обработки, температуру режущей части резца замеряем каждые 15 минут. Полученные данные сводим в таблицу 8.15.

Таблица 8.15

№

Температура, град С⁰

Рисунок 8.4 – График изменения температуры

После построения графика (Рисунок 8.4.), получили уравнение зависимости,

Это уравнение четвертой степени, приближение формулы к экспериментальным данным очень хорошее, коэффициент детерминации равен R² = 0,9945. Из анализа графика и уравнения видно, что до 8 точки графика (120 минут работы резца) температура в пределах нормы, но после этого температура резца начинает резко возрастать, но после 11 точки скорость повышения температуры замедляется.

Пример. В лаборатории проводят эксперимент с новым пищевым продуктом. В этом продукте имеется сахар, в процессе химической реакции количество сахара меняется. Пробы берутся через каждые 10 минут, величина пробы 1 кг. Количество сахара определяется в граммах. Данные опыта сведены в таблицу 8.16.

Таблица 8.16 – Содержание сахара в пробе

№	замер	№	замер	№	замер
	2,1		1,2
	2,4		1,3		6,2
	2,6		1,3
	2,9		1,4		5,2
			1,5		4,2
	2,8		1,8		3,4
	2,4		2,1		3,1
			2,5		3,1
	1,9		3,4		3,2
	1,5		4,2		3,1

Рисунок 8.5- График зависимость количества сахара от времени реакции, сахар- граммы.

По данным был построен график (Рисунок 8.5.), затем получена аналитическая формула зависимости концентрации сахара от времени. Это уравнение:

Коэффициент детерминации равен

Получили очень сложную зависимость, она выражается уравнением шестой степени. Приближенность уравнения к реальности достаточно высокая.

Программа EXCEL позволяет получать не только полиноминальные уравнения, но и другие зависимости.

Пример. Производится испытание мельницы. В процессе работы меняется частота вращения вала, при этом производится замер тонкости помола (дисперсность) сырья- руды (Таблица 8.17.)

Таблица 8.17- Результаты исследования

Частота, об/мин	Дисперсность, мкм

На рисунке 8.6А был выбран тренд степенной функции, получено соответствующее уравнение функции, на рисунке 8.6Б был выбран тренд полиноминальной квадратической функции и получено соответствующее уравнение. Коэффициент детерминации полиноминальной функции больше (0,996 против 0,9772), следовательно, полиноминальная функция описывает процесс лучше.

Рисунок 8.6 – Два графика одного процесса, описанные разными функциями

Множественный анализ. Этот анализ определяет аналитическое выражение функции нескольких аргументов. Методика его проведения более сложна и также может проводиться с помощью EXCEL.

Обычно уравнение множественной регрессии выглядит следующим образом - это уравнение линейной регрессии.

(8.5.)

Также, исследуемый процесс может описываться экспоненциальным уравнением:

(8.6.)

Задача исследования найти значения коэффициентов при Х и свободного члена В. В программе EXCEL есть специальные программы для решения этой задачи. Это программа ЛИНЕЙН(известные значения y; известные значения x; конст; статистика), которая определяет значения в уравнении (10.17.) и программа ЛГРФПРИБЛ(известные значения y; известные значения x; конст; статистика) для уравнения (10.18.). В программу вводят известные значения функции Y, затем известные значения аргумента Х, затем значение – конст, которое может принимать два значения: «ИСТИНА» - в этом случае в уравнении регрессии будет присутствовать значение свободного члена В, «ЛОЖЬ» - свободного члена В не будет, значение – статистика, оно также имеет два значения: «ИСТИНА» - определяются значения ошибок для коэффициентов и свободного члена, «ЛОЖЬ» - значения не определяются. В таблице 8.18. показано размещение полученных данных расчета.

Таблица 8.18- Размещение данных расчета

A	B	C	D	E	F
M_n	Mn-1	….	M₂	M₁	В
Sen	Sen-1	…	Se2	Se1	Seb
R2	Sey
F	df
SSper	SSост

1-я строка – указаны коэффициенты M при Х, причем порядок коэффициентов начинается с предпоследней графы – М1 и считается справа налево к Мn (М1 коэффициент при Х1, М2 – коэффициент при Х2 и т.д.). В последней графе дается значение свободного члена В. 2-я – указаны значения стандартных ошибок для коэффициентов М и свободного члена В. Стандартные ошибки определяют уровень колебания параметра. 3-я – указаны коэффициент детерминации R2 и стандартная ошибка для функции Y. 4-я - указаны F-статистика, или F-наблюдаемое значение. F-статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет. dF- степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. 5-я - SSper регрессионная сумма квадратов, SSост остаточная сумма квадратов

Пример. Имеем параметр качества – шероховатость обработки детали Ra. Чем это параметр меньше, тем качество выше. Необходимо провести регрессионный анализ и получить уравнение регрессии. Определены 6 основных фактора, влияющих на шероховатость.

1. Скорость резания V (м/сек)- Х1. 2. Концентрация керосина в СОЖ (смазывающее- охлаждающая жидкость) (%) – Х2. 3. Процент углерода в стали заготовки (%) – Х3. 4. Срок эксплуатации станка (месяцы) – Х4. 5. Подача режущего инструмента (мм/мин) – Х5. 6. Припуск (мм) –Х6.

2. Проведены эксперименты, собраны данные (Таблица 8.19.)

Таблица 8.19- Результаты эксперимента и расчета

№№	Х1	Х2	Х3	Х4	Х5	Х6	Ra, Y	Y(10.16)	Y (10.17)
			1,5			0,7		19,7577	19,9884
			1,9		6,5	1,0		24,0931	23,6218
			1,7			1,2		27,0348	26,8185
			2,0			1,0		25,8979	25,5746
			2,1			1,5		32,7668	33,6392
			1,4		4,5	0,8		19,0016	19,0267
			1,8			1,0		25,6985	25,9143
			1,2		5,5	1,1		23,8753	23,6546
			1,5		8,5	1,4		29,8743	29,7026
		Коэффициент детерминации R²	0,97511	0,95327

Данные таблицы 8.19. вводим в программу EXCEL, в ячейке A11 набираем оператор ЛИНЕЙН. Вводим значения Y (G2:G9), затем вводим значения Х (A1:F9) и дважды вводим значение параметра «ИСТИНА». После этого обозначаем массив данных – выделяем область А11-G11 –А15-G15 (необходимо выделить область 5 строк вниз от строки, где вводится оператор ЛИНЕЙН и по горизонтали область равную количеству Х плюс 1 (Рисунок 8.7.)

После этого нажимаем клавишу F2 и после этого Ctrl+Shift+Enter. Получаем результаты расчета, как показано на рисунке 8.7. Первая строка (А11-G11) полученных данных показывает коэффициенты М при Х и свободный член В.

Рисунок 8.7 – Проведение регрессионного анализа в программе EXCEL

Программа ЛГРФПРИБЛ вычисляется аналогично.Можем составить уравнение регрессии:

Линейная (уравнение 8.5.)

Экспоненциальная (уравнение 8.6.)

По данным формулам получены значения функции Y, они внесены в крайние правые столбцы таблицы 8.19. Как видно эти значения практически совпали с экспериментальными значениями Y.

Из полученных формул можно сделать следующие выводы:

1. На увеличение значения Y самое сильное влияние оказывает Х₆, а на уменьшение величины Y влияет увеличение значения Х₃.

2. Меньше всего на изменение значения Y оказывает Х₁

Каждое из этих уравнений достаточно хорошо отмечает практические точки, по которым были получены уравнения. Но задача аналитического выражения (формулы) показывать теоретические значения функции (Y), которые максимально точно отражали значения практических значений, которые еще не известны. Имея полученные уравнения зависимости параметра шероховатости, мы можем, подставляя необходимые значения Х, заранее знать какое значение шероховатости получим, правда с некоторой погрешностью.

Разработка экспериментов

Разработка экспериментов носит научный исследовательский характер. В экспериментальных условиях мы статистически исследуем факторы, влияющие на процесс и в конечном итоге на качество продукции. Эксперименты позволяют нам смоделировать, оценить и проверить свои гипотезы в контролируемых условиях, и лишь затем реализовать их практически, что экономит наше время и деньги.

Для эффективности экспериментов проводить их надо системно и грамотно. Время и деньги, выделяемые на эксперимент, необходимо расходовать оптимально, с максимальным эффектом. Надо всегда помнить, что результаты плохо разработанного эксперимента могут дать вам недостоверные результаты, что приведет вас к неверным выводам и выполнению ненужных вредных действий.

Для проведения эксперимента необходимо иметь программу его проведения. План составления программы эксперимента:

1. Определите проблему, которую вы хотите исследовать через эксперимент. Должны быть точно определены количественные критерии проблемы, их недостатки, результаты, которые необходимо получить после решения.

2. Определите задачи эксперимента. Цель эксперимента, входные данные, выходные данные.

3. Разработка методики эксперимента. Необходимо точно разработать методы проведения эксперимента, их последовательность, порядок расчета.

4. Разработка плана. Детально проанализируйте среду, предпосылки и условия, которые будут способствовать или мешать эксперименту, разработайте план, позволяющий решить задачи за выделенное время, в пределах выделенных ресурсов. Разработайте план сбора данных, чтобы ваша измерительная система обеспечила сбор всей необходимой информации, план анализа данных для правильного объяснения результатов.

Здесь был показан самый простой двухфакторный эксперимент. С приобретением опыта и знаний можно применять более сложные и эффективные методы планирования эксперимента.

1. Анализ кривых. Метод 2-х факторного эксперимента основан на предположении о линейной зависимости между факторами и откликами. Но часто зависимости носят более сложный характер, который выражается нелинейными зависимостями. В этом случае график зависимости носит криволинейный характер. В этом случае необходим эксперимент, который позволил бы обнаружить криволинейность зависимости. Обычно это делают, включая в каждый экспериментальный фактор более двух уровней.

2. Повторения. При повторении эксперимента получают несколько другие результаты. Это неудивительно, вариация существует везде. Повторные испытания позволяют оценить достоверность результатов, уровень колебания результатов, их достоверность.

3. Дисперсионный анализ. Почти все эксперименты включают поиск, исследование и сравнение источников получаемой вариации. Дисперсионный анализ – это мощный метод, позволяющий охарактеризовать и количественно оценить различные источники вариации.

4. Устойчивость. Способность процесса или системы показывать стабильные результаты, несмотря на вариацию, называется устойчивостью. Существуют экспериментальные схемы, которые минимизируют влияние вариации, и следовательно дают достоверные результаты о поведении исследуемой системы.

5. Методы поверхности откликов и оптимизация. Цель многих экспериментов – найти лучшие значения для входных переменных. Целая отрасль плановых экспериментов направлена на поиск локальных или глобальных настроек для оптимальной работы.

6. Дробные факторные эксперименты. Полные 2^к – факторные эксперименты можно адаптировать для более эффективного поиска среди большого количества экспериментальных факторов. При увеличении количества последних приходится жертвовать точностью. Решить эту проблему позволяют дробные факторные эксперименты, которые представляют собой адаптацию полных 2^к – факторных экспериментов и позволяют извлечь максимальную пользу из поиска.

⇐ Предыдущая 1 2 3 4 56

Воспользуйтесь поиском по сайту: