 |
Действие статистических функций на матрицы
|
|
|
|
Все рассмотренные примеры работы статистических функций относились к векторам, элементы которых были случайными числами. Но точно так же все эти функции применяются и по отношению к выборкам случайных данных, сгруппированных в матрицы. При этом статистические характеристики рассчитываются для совокупности всех элементов матрицы, без разделения ее на строки и столбцы. Например, если матрица имеет размерность MXN, то и объем выборки будет равен M-N.
Соответствующий пример вычисления среднего значения приведен в листинге 14.16. В его первой строке определяется матрица данных х размера 4x2. Действие встроенной функции mean матричного аргумента (последняя строка листинга) иллюстрируется явным суммированием элементов матрицы х (предпоследняя строка). Действие прочих встроенных функций на матрицы совершенно аналогично действию их на векторы (листинг 14.17).
Листинг 14.16. Вычисление среднего значения элементов матрицы

Листинг 14.17. Действие различных статических функций на матрицу
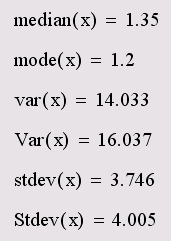
Некоторые статистические функции (например, вычисления ковариации) имеют два аргумента. Они также могут быть матрицами, но, в соответствии со смыслом функции, должны иметь одинаковую размерность.
Большинству статистических функций позволяется иметь в качестве аргументов даже не одну матрицу, а любое количество матриц, векторов и скаляров. Числовые характеристики будут рассчитаны для всей совокупности значений аргументов функции. Соответствующий пример приведен в листинге 14.18.
Листинг 14.18. Статические функции нескольких аргументов
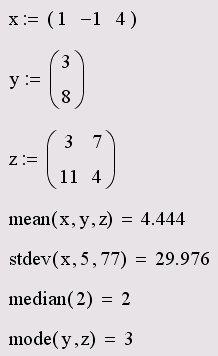
Случайные процессы
Встроенные функции для генерации случайных чисел создают выборку из случайных данных АХ. Часто требуется создать непрерывную или дискретную случайную функцию A(t) одной или нескольких переменных (случайный процесс или случайное поле), значения которой будут упорядочены относительно своих переменных Создать псевдослучайный процесс можно способом, представленным в листинге 14 19
|
|
|
Листинг 14.19. Генерация псевдослучайного процесса

В первой строке листинга 14 19 определено количество N независимых случайных чисел, которые будут впоследствии сгенерированы, и радиус временной корреляции т В следующих трех строках определяются моменты времени тэ, которым будут отвечать случайные значения A(t.,) Создание нормального случайного процесса сводится к генерации обычным способом вектора независимых случайных чисел х и построению интерполяционной зависимости в промежутках между ними. В листинге 14.19 используется сплайн-интерполяция.

Рис. 14.14. Псевдослучайный процесс (листинг 14.19)
В результате получается случайный процесс A(t), радиус корреляции которого определяется расстоянием т между точками, для которых строится интерполяция. График случайного процесса A(t) вместе с исходными случайными числами показан на рис. 14.14. Случайное поле можно создать несколько более сложным способом с помощью многомерной интерполяции.
К случайным процессам, сгенерированным таким способом, как и к данным эксперимента, применяются любые статистические методы обработки, например корреляционный или спектральный анализ. Приведем в качестве примера листинг 14.20, показывающий, как организовать расчет корреляционной функции случайного процесса.
Листинг 14.20. Дискретизация случайного процесса и вычисление корреляционной функции (продолжение листинга 14.19)
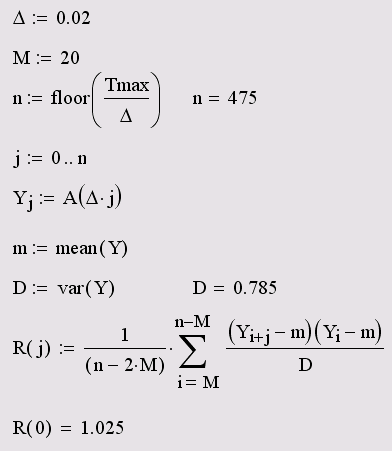
Дискретизация интервала <0,Tmax) для случайного процесса A(t) произведена с различным элементарным интервалом А (первая строка листинга). В зависимости от значения А, получается различный объем п выборки случайных чисел YL являющихся значениями случайной функции A(t) в точках дискретизации. В последних четырех строках определяются различные характеристики случайной величины Y, являющиеся, по сути, характеристиками случайного процесса A(t). График рассчитанной в 2 M+1 точках корреляционной функции R(j) показан на рис. 14.15.
|
|
|
Внимательному читателю предлагается самостоятельно ответить на вопрос: почему при таком расчете корреляционной функции ее значение R(0) не равно 1, как должно быть по определению?

Рис. 14.15. Корреляционная функция (листинги 14.19—14.20)
Некоторые примеры
Приведем два характерных статистических примера, которые легко решаются с помощью Mathcad.
|
|
|


