 |
Экстраполяция функцией предсказания
|
|
|
|
Все рассмотренные выше функции осуществляли экстраполяцию данных за пределами их интервала с помощью соответствующей зависимости, основанной на анализе расположения нескольких исходных точек на границах интервала. В Mathcad имеется более развитый инструмент экстраполяции, который учитывает распределение данных вдоль всего интервала. В функцию predict встроен линейный алгоритм предсказания поведения функции, основанный на анализе, в том числе осцилляции.
· predict (у,m,n) — функция предсказания вектора, экстраполирующего выборку данных;
· у — вектор действительных значений, взятых через равные промежутки значений аргумента;
· m — количество последовательных элементов вектора у, согласно которым строится экстраполяция;
· n— количество элементов вектора предсказаний.
Пример использования функции предсказания на примере экстраполяции осциллирующих данных yi с меняющейся амплитудой приведен в листинге 15.4. Полученный график экстраполяции, наряду с самой функцией, показан на рис. 15.8. Аргументы и принцип действия функции predict отличаются от рассмотренных выше встроенных функций интерполяции-экстраполяции. Значений аргумента для данных не требуется, поскольку по определению функция действует на данные, идущие друг за другом с равномерным шагом. Обратите внимание, что результат функции predict вставляется "в хвост" исходных данных.
Листинг 15.4. Экстраполяция при помощи функции предсказания

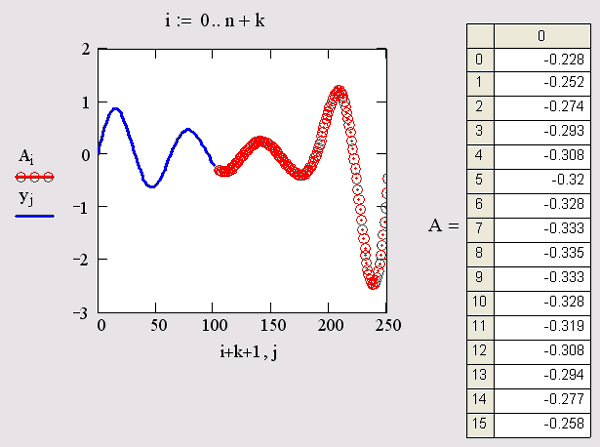
Рис. 15.8. Экстраполяция при помощи функции предсказания (листинг 15.4)
Как видно из рис. 15.9, функция предсказания может быть полезна при экстраполяции данных на небольшие расстояния. Вдали от исходных данных результат часто бывает неудовлетворительным. Кроме того, функция predict хорошо работает в задачах анализа подробных данных с четко прослеживающейся закономерностью (типа рис. 15.8), в основном осциллирующего характера.
|
|
|
Если данных мало, то предсказание может оказаться бесполезным. В листинге 15.5 приведена экстраполяция небольшой выборки данных (из примеров, рассмотренных в предыдущих разделах). Соответствующий результат показан на рис. 15.9 для различных крайних точек массива исходных данных, для которых строится экстраполяция.
Листинг 15.5. Экстраполяция при помощи функции предсказания


Рис. 15.9. Работа функции предсказания в случае малого количества данных (листинг 15.5)
Многомерная интерполяция
Двумерная сплайн-интерполяция приводит к построению поверхности z(x,y), проходящей через массив точек, описывающий сетку на координатной плоскости (х,у). Поверхность создается участками двумерных кубических сплайнов, являющихся функциями (х,у) и имеющих непрерывные первые и вторые производные по обеим координатам.
Многомерная интерполяция строится с помощью тех же встроенных функций, что и одномерная, но имеет в качестве аргументов не векторы, а соответствующие матрицы. Существует одно важное ограничение, связанное с возможностью интерполяции только квадратных N*N массивов данных.
· interp(s,x,z,v) — скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами;
· s — вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline;
· х — матрица размерности Nx2, определяющая диагональ сетки значений аргумента (элементы обоих столбцов соответствуют меткам х и у и расположены в порядке возрастания);
· z — матрица действительных данных размерности NXN;
· v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.
|
|
|
Вспомогательные функции построения вторых производных имеют те же матричные аргументы, что и interp: lspline (X,Y), pspline (X, У), cspline(X,Y).
Пример исходных данных приведен на рис. 15.10 в виде графика линий уровня, программная реализация двумерной интерполяции показана в листинге 15.6, а ее результат — на рис. 15.11.
Листинг 15.6. Двумерная интерполяция


Рис. 15.10. Исходное двумерное поле данных (листинг 15.6)

Рис. 15.11. Результат двумерной интерполяции (листинг 15.6)
Регрессия
Задачи математической регрессии имеют смысл приближения выборки данных (Xi..Yi) некоторой функцией f(х), определенным образом минимизирующей совокупность ошибок |f(xi)-yi|. Регрессия сводится к подбору неизвестных коэффициентов, определяющих аналитическую зависимость f(х). В силу производимого действия большинство задач регрессии являются частным случаем более общей проблемы сглаживания данных.
Как правило, регрессия очень эффективна, когда заранее известен (или, по крайней мере, хорошо угадывается) закон распределения данных (xi, yi).
Линейная регрессия
Самый простой и наиболее часто используемый вид регрессии — линейная. Приближение данных (xi, yi) осуществляется линейной функцией у(х)=b+ах. На координатной плоскости (х,у) линейная функция, как известно, представляется прямой линией (рис. 15.12). Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты а и b вычисляются из условия минимизации суммы квадратов ошибок |b+axi-yi|.
Чаще всего такое же условие ставится и в других задачах регрессии, т. е. приближения массива данных (хi,уi) другими зависимостями у(х). Исключение рассмотрено в листинге 15.9.

Рис. 15.12. Линейная регрессия (листинг 15.7 или 15.8)
Для расчета линейной регрессии в Mathcad имеются два дублирующих друг друга способа. Правила их применения представлены в листингах 15.7 и 15.8. Результат обоих листингов получается одинаковым (рис. 15.12).
· line(x,y) — вектор из двух элементов (b,а) коэффициентов линейной регрессии b+а-х;
· intercept (x,y) — коэффициент b линейной регрессии;
· slope(x,y) — коэффициент а линейной регрессии;
· х — вектор действительных данных аргумента;
· у — вектор действительных данных значений того же размера.
|
|
|
Листинг 15.7. Линейная регрессия
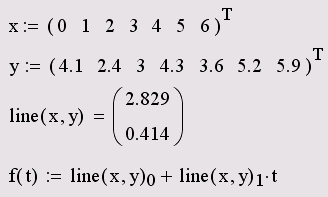
Листинг 15.8. Другая форма записи линейной регрессии

В Mathcad имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную регрессию для расчета коэффициентов а и b (листинг 15.9).
· medfit(x,y) — вектор из двух элементов (b,а) коэффициентов линейной медиан-медианной регрессии b+ах;
· х,у — векторы действительных данных одинакового размера.
Листинг 15.9. Построение линейной регрессии двумя разными методами (продолжение листинга 15.7)

Различие результатов среднеквадратичной и медиан-медианной регрессии иллюстрируется рис. 15.13.
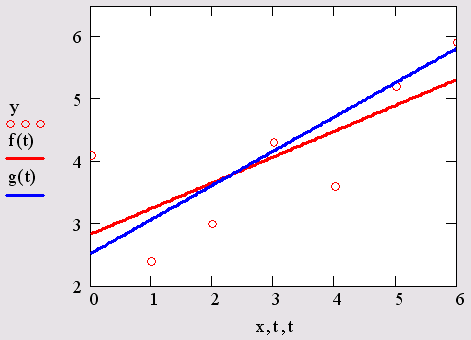
Рис. 15.13. Линейная регрессия по методу наименьших квадратов и методу медиан (листинги 15.7 и 15.9)
Полиномиальная регрессия
В Mathcad реализована регрессия одним полиномом, отрезками нескольких полиномов, а также двумерная регрессия массива данных.
Полиномиальная регрессия
Полиномиальная регрессия означает приближение данных (xi, yi) полиномом k-й степени А(х)=а+bх+сх2+dх3+...+hxk (рис. 15.14). При k=1 полином является прямой линией, при k=2 — параболой, при k=3 — кубической параболой и т. д. Как правило, на практике применяются k<5.
Для построения регрессии полиномом k-й степени необходимо наличие, по крайней мере (k+1) точек данных.
В Mathcad полиномиальная регрессия осуществляется комбинацией встроенной функции regress и полиномиальной интерполяции.
· regress(x,y,k) — вектор коэффициентов для построения полиномиальной регрессии данных;
· interp(s,x,y, t) — результат полиномиальной регрессии;
· s=regress(x,y,k);
· х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
· у — вектор действительных данных значений того же размера;
· k — степень полинома регрессии (целое положительное число);
· t — значение аргумента полинома регрессии.
Для построения полиномиальной регрессии после функции regress Вы обязаны использовать функцию interp.

Рис. 15.14. Регрессия полиномами разной степени (коллаж результатов листинга 15.10 для разных k)
|
|
|
Пример полиномиальной регрессии квадратичной параболой приведен в листинге 15.10.
Листинг 15.10. Полиноминальная регрессия

|
|
|


