 |
Интервальная оценка дисперсии
|
|
|
|
Требуется определить числовой интервал (L,U), внутри которого будет лежать с вероятностью 1-сс=75% дисперсия нормальной случайной величины, исходя из объема выборки в N чисел. Эта задача решается в статистике с помощью х2-распределения (листинг 14.21).
Листинг 14.21. Интервальное оценивание дисперсии 1

Указанный интервал называется (1-а)% доверительным интервалом. Обратите внимание на использование при решении данной задачи функции stdev (с прописной буквы) для расчета выборочного стандартного отклонения. В статистике часто встречаются выражения, которые более удобно записывать через функции в такой нормировке, именно для этого они и появились в Mathcad.
Проверка статистических гипотез
В статистике рассматривается огромное число задач, связанных с проверкой тех или иных гипотез н. Разберем пример простой гипотезы. Пусть имеется выборка N чисел с нормальным законом распределения и неизвестными дисперсией и математическим ожиданием. Требуется принять или отвергнуть гипотезу н о том, что математическое ожидание закона распределения равно некоторому числу m0=0.2.
Задачи проверки гипотез требуют задания уровня критерия проверки гипотезы а, который описывает вероятность ошибочного отклонения истинной н. Если взять а очень малым, то гипотеза, даже если она ложная, будет почти всегда приниматься; если, напротив, взять а близким к 1, то критерий будет очень строгим, и гипотеза, даже верная, скорее всего, будет отклонена. В нашем случае гипотеза состоит в том, что цо=о.2, а альтернатива — что m0=0.2. Оценка математического ожидания, как следует из курса классической статистики, решается с помощью распределения Стьюдента с параметром N-1 (этот параметр называется степенью свободы распределения).
|
|
|
Для проверки гипотезы (листинг 14.22) рассчитывается (а/2) — квантиль распределения Стьюдента т, который служит критическим значением для принятия или отклонения гипотезы. Если соответствующее выборочное значение t по модулю меньше т, то гипотеза принимается (считается верной). В противном случае гипотезу следует отвергнуть.
Листинг 14.22. Проверка гипотезы о математическом ожидании при неизвестной дисперсии

В последней строке листинга вычисляется истинность или ложность условия, выражающего решение задачи. Поскольку условие оказалось ложным (равным не 1, а 0), то гипотезу необходимо отвергнуть.
На рис. 14.16 показано распределение Стьюдента с N-1 степенью свободы вместе с критическими значениями, определяющими соответствующий интервал. Если t (оно тоже показано на графике) попадает в него, то гипотеза принимается; если не попадает (как произошло в данном случае) — отвергается. Если увеличить а, ужесточив критерий, то границы интервала будут сужаться, по сравнению с показанными на рисунке.
В листинге 14.23 приводится альтернативный способ проверки той же самой гипотезы, связанный с вычислением значения не квантиля, а самого распределения Стьюдента.

Рис. 14.16. К задаче проверки статистических гипотез (листинг 14.22)
Листинг 14.23. Другой вариант проверки гипотезы (продолжение листинга 14.22)

Мы разобрали только два характерных примера статистических вычислений. Однако с помощью Mathcad легко решаются самые разнообразные задачи математической статистики.
Большое количество задач разобрано в Ресурсах в рубрике Statistics (Статистика) справочной системы Mathcad.
Обработка данных
Интерполяция
Когда Вы имеете дело с выборкой экспериментальных данных, то они, чаще всего, представляются в виде массива, состоящего из пар чисел (xi, yi). Поэтому возникает задача аппроксимации дискретной зависимости y(x) непрерывной функцией f(x). Функция f(x), в зависимости от специфики задачи, может отвечать различным требованиям:
|
|
|
· f(x) должна проходить через точки (xi, yi), т.е. f (хi)=уi, i=1...n. В этом случае говорят об интерполяции данных функцией f(х) во внутренних точках между хi, или экстраполяции за пределами интервала, содержащего все хi;
· f (х) должна некоторым образом (например, в виде определенной аналитической зависимости) приближать y(xi), не обязательно проходя через точки (xi, yi). Такова постановка задачи регрессии, которую во многих случаях также можно назвать сглаживанием данных;
· f (х) должна приближать экспериментальную зависимость y(xi), учитывая к тому же, что данные (xi, yi) получены с некоторой погрешностью, выражающей шумовую компоненту измерений. При этом функция f (х), с помощью того или иного алгоритма, уменьшает погрешность, присутствующую в данных (xi, yi). Такого типа задачи называют задачами фильтрации. Сглаживание — частный случай фильтрации.
Различные виды построения аппроксимирующей зависимости f (х) иллюстрирует рис. 15.1. На нем исходные данные обозначены кружками, интерполяция отрезками прямых линий — пунктиром, линейная регрессия — наклонной прямой линией, а фильтрация — жирной гладкой кривой. Эти зависимости приведены в качестве примера и отражают лишь малую часть возможностей Mathcad по обработке данных. Вообще говоря, в Mathcad имеется целый арсенал встроенных функций, позволяющий осуществлять самую различную регрессию, интерполяцию-экстраполяцию и сглаживание данных.

Рис. 15.1. Разные задачи аппроксимации данных
Как в целях подавления шума, так и для решения других проблем обработки данных, широко применяются различные интегральные преобразования. Они ставят в соответствие всей совокупности данных у(х) некоторую функцию другой координаты (или координат) F(CO). Примерами интегральных преобразований являются преобразование Фурье и вейвлетное преобразование. Напомним, что некоторые преобразования, например Фурье и Лапласа, можно осуществить в режиме символьных вычислений. Каждое из интегральных преобразований эффективно для решения своего круга задач анализа данных.
|
|
|
Для построения интерполяции-экстраполяции в Mathcad имеются несколько встроенных функций, позволяющих "соединить" точки выборки данных (xi, yi) кривой разной степени гладкости. По определению интерполяция означает построение функции f(х), аппроксимирующей зависимость у(х) в промежуточных точках (между xi). Поэтому интерполяцию еще по-другому называют аппроксимацией. В точках xi значения интерполяционной функции должны совпадать с исходными данными, т. е. A(xi) =у(xi).
Везде в этом разделе при рассказе о различных типах интерполяции будем использовать вместо обозначения А(x) другое имя ее аргумента A(t), чтобы не путать вектор данных х и скалярную переменную t.
Линейная интерполяция
Самый простой вид интерполяции — линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии. Интерполирующая функция А(Х) состоит из отрезков прямых, соединяющих точки (рис. 15.2).
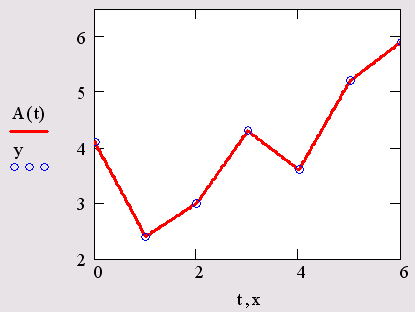
Рис. 15.2. Линейная интерполяция (листинг 15.1)
Для построения линейной интерполяции служит встроенная функция linterp (листинг 15.1).
· linterp(x, y, t) — функция, аппроксимирующая данные векторов х и у кусочно-линейной зависимостью;
- х — вектор действительных данных аргумента;
- у — вектор действительных данных значений того же размера;
- t — значение аргумента, при котором вычисляется интерполирующая функция.
Элементы вектора х должны быть определены в порядке возрастания, т. е. Х1<Х2<Х3<... <Xn.
Листинг 15.1. Линейная интерполяция

Как видно из листинга, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
· Введите векторы данных х и у (первые две строки листинга).
· Определите функцию linterp(х,у, t).
· Вычислите значения этой функции в требуемых точках, например lin-terp(x,y, 2.4)=3.52 или linterp(x,y,6) =5.9, или постройте ее график, как показано на рис. 15.2.
Обратите внимание, что функция A(t) на графике имеет аргумент t, а не х. Это означает, что функция А(t) вычисляется не только при значениях аргумента (т. е. в семи точках), а при гораздо большем числе аргументов в интервале (0,6), что автоматически обеспечивает Mathcad. Просто в данном случае эти различия незаметны, т. к. при обычном построении графика функции А(х) от векторного аргумента х (рис. 15.3) Mathcad, по умолчанию, соединяет точки графика прямыми линиями (т. е. скрытым образом осуществляет их линейную интерполяцию).
|
|
|

Рис. 15.3. Обычное построение графика функции от векторной переменной х (листинг 15.1)
|
|
|


