 |
Встроенные функции для сглаживания
|
|
|
|
В Mathcad имеется несколько встроенных функций, реализующих различные алгоритмы сглаживания данных.
· medsmooth(y,b) — сглаживание алгоритмом "бегущих медиан";
· ksmooth(x,y,b) — сглаживание на основе функции Гаусса;
· supsmooth(x,y) — локальное сглаживание адаптивным алгоритмом, основанное на анализе ближайших соседей каждой пары данных;
· х — вектор действительных данных аргумента (для supsmooth его элементы должны быть расположены в порядке возрастания);
· у — вектор действительных значений того же размера, что и х;
· b — ширина окна сглаживания.
Все функции имеют в качестве аргумента векторы, составленные из массива данных, и выдают в качестве результата вектор сглаженных данных того же размера. Функция medsmooth предполагает, что данные расположены равномерно.
Подробную информацию об алгоритмах, заложенных в функции сглаживания, Вы найдете в справочной системе Mathcad в статье Smoothing (Сглаживание), находящейся в разделе Statistics (Статистика).
Часто бывает полезным совместить сглаживание с последующей интерполяцией или регрессией. Соответствующий пример приведен в листинге 15.16 для функции supsmooth. Результат работы листинга показан на рис. 15.18 (кружки обозначают исходные данные, крестики — сглаженные, пунктирная кривая — результат сплайн-интерполяции). Сглаживание тех же данных при помощи "бегущих медиан" и функции Гаусса с разным значением ширины окна пропускания показаны на рис. 15.19 и 15.20, соответственно.
Листинг 15.16. Сглаживание с последующей сплайн-интерполяцией


Рис. 15.18. Адаптивное сглаживание (листинг 15.16)
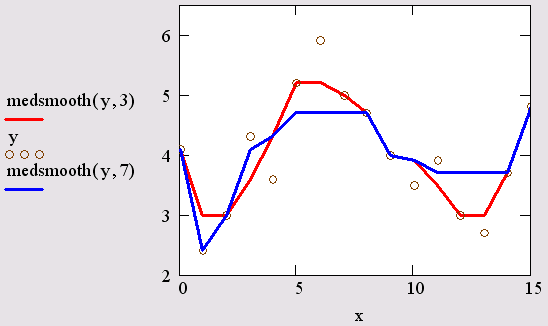
Рис. 15.19. Сглаживание "бегущими медианами"

Рис. 15.20. Сглаживание при помощи функции ksmooth
|
|
|
Скользящее усреднение
Помимо встроенных в Mathcad, существует несколько популярных алгоритмов сглаживания, на одном из которых хочется остановиться особо. Самый простой и очень эффективный метод — это скользящее усреднение. Его суть состоит в расчете для каждого значения аргумента среднего значения по соседним w данным. Число w называют окном скользящего усреднения; чем оно больше, тем больше данных участвуют в расчете среднего, тем более сглаженная кривая получается. На рис. 15.21 показан результат скользящего усреднения одних и тех же данных (кружки) с разным окном w=3

Рис. 15.21. Скользящее усреднение с разными w=3,5,15 (листинг 15.17, коллаж трех графиков)
(пунктир), w=5 (штрихованная кривая) и w=is (сплошная кривая). Видно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших w — отражают лишь закономерность их медленных вариаций.
Чтобы реализовать в Mathcad скользящее усреднение, достаточно очень простой программы, приведенной в листинге 15.17. Она использует только значения у, оформленные в виде вектора, неявно предполагая, что они соответствуют значениям аргумента х, расположенным через одинаковые промежутки Вектор х применялся лишь для построения графика результата (рис 15.21)
Листинг 15.17. Сглаживание скользящим усреднением

Приведенная программная реализация скользящего усреднения самая простая, но не самая лучшая Возможно Вы обратили внимание, что все кривые скользящего среднего на рис 15.21 слегка "обгоняют" исходные данные Почему так происходит, понятно согласно алгоритму, заложенному в последнюю строку листинга 15.17, скользящее среднее для каждой точки вычисляется путем усреднения значений предыдущих w точек Чтобы результат скользящего усреднения был более адекватным лучше применить центрированный алгоритм расчета по w/2 предыдущим и w/2 последующим значениям Он будет немного сложнее, поскольку придется учитывать недостаток точек не только в начале (как это сделано в программе с помощью функции условия if) но и в конце массива исходных данных.
|
|
|
Устранение тренда
Еще одна типичная задача возникает, когда интерес исследований заключается не в анализе медленных (или низкочастотных) вариаций сигнала у(х) (для чего применяется сглаживание данных), а в анализе быстрых его изменений Часто бывает, что быстрые (или высокочастотные) вариации накладываются определенным образом на медленные, которые обычно называют трендом. Часто тренд имеет заранее предсказуемый вид, например линейный. Чтобы устранить тренд, можно предложить последовательность действий, реализованную в листинге 15.18.
· Вычислить регрессию f(x), например линейную, исходя из априорной информации о тренде (предпоследняя строка листинга).
· Вычесть из данных у (х) тренд f (x) (последняя строка листинга).
Листинг 15.18. Устранение тренда

На рис. 15.22 показаны исходные данные (кружками), выделенный с помощью регрессии линейный тренд (сплошной прямой линией) и результат устранения тренда (пунктир, соединяющий крестики).

Рис. 15.22. Устранение тренда (листинг 15.18)
Полосовая фильтрация
В предыдущих разделах была рассмотрена фильтрация быстрых вариаций сигнала (сглаживание) и его медленных вариаций (снятие тренда). Иногда требуется выделить среднемасштабную составляющую сигнала, уменьшив как более быстрые, так и более медленные его компоненты. Одна из возможностей решения этой задачи связана с применением полосовой фильтрации на основе последовательного скользящего усреднения.

Рис. 15.23. Результат полосовой фильтрации (листинг 15.19)
Алгоритм полосовой фильтрации приведен в листинге 15.19, а результат его применения показан на рис. 15.23 сплошной кривой. Алгоритм реализует такую последовательность операций:
· Приведение массива данных y к нулевому среднему значению путем его вычитания из каждого элемента у (третья и четвертая строки листинга).
· Устранение из сигнала у высокочастотной составляющей, имеющее целью получить сглаженный сигнал middle, например с помощью скользящего усреднения с малым окном w (в листинге 15.19 w=3).
|
|
|
· Выделение из сигнала middle низкочастотной составляющей slow, например, путем скользящего усреднения с большим окном w (в листинге 15.19 w=7) либо с помощью снятия тренда (см. разд. 15.3.3).
· Вычитание из сигнала middle тренда slow (последняя строка листинга), тем самым выделяя среднемасштабную составляющую исходного сигнала у.
Листинг 15.19. Полосовая фильтрация

|
|
|


