 |
Регрессия специального вида
|
|
|
|
Кроме рассмотренных, в Mathcad встроено еще несколько видов трехпара-метрической регрессии. Их реализация несколько отличается от приведенных выше вариантов регрессии тем, что для них, помимо массива данных, требуется задать некоторые начальные значения коэффициентов а,b,с. Используйте соответствующий вид регрессии, если хорошо представляете себе, какой зависимостью описывается Ваш массив данных. Когда тип регрессии плохо отражает последовательность данных, то ее результат часто бывает неудовлетворительным и даже сильно различающимся в зависимости от выбора начальных значений. Каждая из функций выдает вектор уточненных параметров а,b,с.
· expfit(x,y,g) —регрессия экспонентой f(x)=aebx+c;
· lgsfit(x,y,g) —регрессия логистической функцией f (x)=a/(1+bесх);
· sinf it (x,y,g) —регрессия синусоидой f(x) =asin(х+b)+с;
· pwfit(x,y,g) — регрессия степенной функцией f(x)=axb+c;
· iogfit(x,y,g) — рефессия логарифмической функцией f(x) =aln(х+b)+с;
· lnfit(x,y) — регрессия двухпараметрической логарифмической функцией f(x)=aln(x)+b;
· х — вектор действительных данных аргумента;
· у — вектор действительных значений того же размера;
· g — вектор из трех элементов, задающий начальные значения а,b,с.
Правильность выбора начальных значений можно оценить по результату регрессии — если функция, выданная Mathcad, хорошо приближает зависимость у (х), значит они были подобраны удачно.
Пример расчета одного из видов трехпараметрической регрессии (экспоненциальной) приведен в листинге 15.13 и на рис. 15.17. В предпоследней строке листинга выведены в виде вектора вычисленные коэффициенты а,b,с, а в последней строке через эти коэффициенты определена искомая функция f (х).
Листинг 15.13. Экспоненциальная регрессия
|
|
|

Многие задачи регрессии данных различными двухпараметрическими зависимостями у (х) можно свести к более надежной, с вычислительной точки зрения, линейной регрессии. Делается это с помощью соответствующей замены переменных.
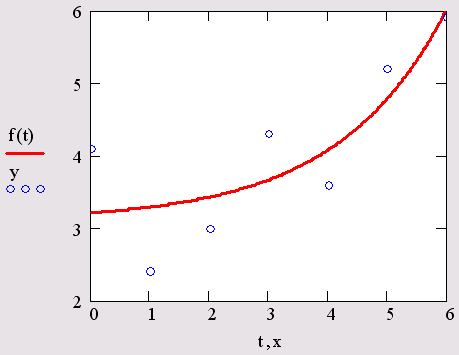
Рис. 15.17. Экспоненциальная регрессия (листинг 15.13)
Регрессия общего вида
В Mathcad можно осуществить регрессию в виде линейной комбинации C1f1(x)+C2f2(х)+,..., где fi(х) — любые функции пользователя, a Ci — подлежащие определению коэффициенты. Кроме того, имеется путь проведения регрессии более общего вида, когда комбинацию функций и искомых коэффициентов задает сам пользователь.
Приведем встроенные функции для регрессии общего вида и примеры их использования (листинги 15.14 и 15.15), надеясь, что читатель при необходимости найдет более подробную информацию об этих специальных возможностях в справочной системе и Mathcad Resources.
· linfit(x,y,F) — вектор параметров линейной комбинации функций пользователя, осуществляющей регрессию данных;
· genfit (x,y,g,G) — вектор параметров, реализующих регрессию данных с помощью функций пользователя общего вида;
· х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
· у — вектор действительных значений того же размера;
· F(X) — пользовательская векторная функция скалярного аргумента;
· g — вектор начальных значений параметров регрессии размерности N;
· G(x,o) — векторная функция размерности N+I, составленная из функции пользователя и ее N частных производных по каждому из параметров C.
Листинг 15.14. Регрессия линейной комбинацией функций пользователи

Листинг 15.15. Регрессия общего вида

Сглаживание и фильтрация
При анализе данных часто возникает задача их фильтрации, заключающаяся в устранении одной из составляющих зависимости y(xi). Наиболее часто целью фильтрации является подавление быстрых вариаций y(xi), которые чаще всего обусловлены шумом. В результате из быстроосциллирующей зависимости y(xi) получается другая, сглаженная зависимость, в которой доминирует более низкочастотная составляющая.
|
|
|
Наиболее простыми и эффективными рецептами сглаживания (smoothing) можно считать регрессию различного вида (см. разд. 15.2). Однако регрессия часто уничтожает информативную составляющую данных, оставляя лишь наперед заданную пользователем зависимость.
Часто рассматривают противоположную задачу фильтрации — устранение медленно меняющихся вариаций в целях исследования высокочастотной составляющей. В этом случае говорят о задаче устранения тренда. Иногда интерес представляют смешанные задачи выделения среднемасштабных вариаций путем подавления как более быстрых, так и более медленных вариаций. Одна из возможностей решения связана с применением полосовой фильтрации.
Несколько примеров программной реализации различных вариантов фильтрации приведены в данном разделе.
|
|
|


