|
Тема 7. Методы расчета однозвенных полнодоступных коммутационных схем при обслуживании потока с повторными вызовами
|
|
|
|
В реальных коммутационных системах вызов, получивший отказ при установлении соединения, осуществляет повторные попытки (вызовы) установления требуемого соединения (рис.7.1). Повторные вызовы возникают не только из-за отсутствия свободных соединительных путей в момент поступления первичного вызова, но и из-за занятости линии вызываемого абонента, неответа вызываемого абонента, ошибок вызывающего абонента в процессе набора номера, неустановления соединения по техническим причинам.
Вызовы, поступающие в коммутационную систему впервые, называются первичными вызовами. В качестве основных характеристик работы однозвенной полнодоступной коммутационной схемы при обслуживании потока с повторными вызовами применяются: 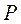 - вероятность потерь первичных вызовов и
- вероятность потерь первичных вызовов и 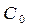 - среднее число повторных вызовов, приходящихся на один первичный вызов.
- среднее число повторных вызовов, приходящихся на один первичный вызов.
Для определения этих характеристик в математической модели с повторными вызовами различают два этапа обслуживания вызова. Первый этап обслуживания характеризуется занятием линии на выходе коммутационной системы независимо от того, чем закончится соединение – разговором, занятостью линии вызываемого абонента и т.д. Второй этап обслуживания характеризуется разговорным состоянием соединения.
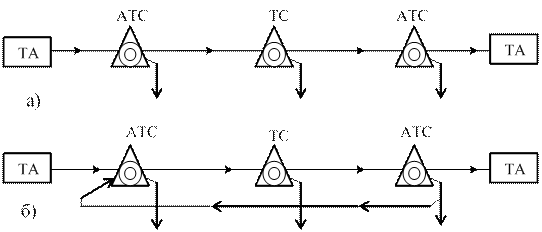
Рис.7.1. Схема установления соединения:
а) без повторных вызовов; б) с повторными вызовами
Вызов считается обслуженным, если он завершился вторым этапом – разговором. Вызов считается не обслуженным, если он завершился первым этапом.
Обозначим вероятность того, что вызов останется не обслуженным через 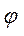 . Эта вероятность может быть определена как доля вызовов, не закончившихся разговором из-за непроизводительного занятия коммутационной системы, т.е.
. Эта вероятность может быть определена как доля вызовов, не закончившихся разговором из-за непроизводительного занятия коммутационной системы, т.е.
|
|
|
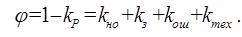 (7.1)
(7.1)
Абоненты, вызовы которых не обслуживаются по причине занятости линий на выходе коммутационной схемы или завершились только первым этапом, являются источниками повторных вызовов. От каждого источника поступают повторные вызовы, образующие поток с параметром 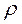 . Величина
. Величина  есть математическое ожидание длительности между двумя соседними попытками установления соединения.
есть математическое ожидание длительности между двумя соседними попытками установления соединения.
Если в течение заданного времени источник не производит повторного вызова, то рассматриваемый вызов теряется окончательно. Это время принимается распределенным по показательному закону с параметром 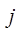 . Тогда среднее время существования источника повторных вызовов
. Тогда среднее время существования источника повторных вызовов 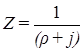 . (7.2)
. (7.2)
При этом с вероятностью 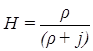 источник производит повторный вызов. Эта вероятность определяет меру настойчивости источника добиться полного обслуживания вызова. Случай Н =0 соответствует схеме рис.7.1.а); случай Н =1 означает, что абонент повторяет попытки установления соединения до тех пор, пока соединение не будет установлено (абсолютная настойчивость абонента).
источник производит повторный вызов. Эта вероятность определяет меру настойчивости источника добиться полного обслуживания вызова. Случай Н =0 соответствует схеме рис.7.1.а); случай Н =1 означает, что абонент повторяет попытки установления соединения до тех пор, пока соединение не будет установлено (абсолютная настойчивость абонента).
Вероятность потери первичного вызова  определяется отношением интенсивности потерянных первичных вызовов по причине отсутствия свободных линий на выходе коммутационной системы в момент поступления первичного вызова к интенсивности поступивших первичных вызовов. При определении среднего числа повторных вызовов
определяется отношением интенсивности потерянных первичных вызовов по причине отсутствия свободных линий на выходе коммутационной системы в момент поступления первичного вызова к интенсивности поступивших первичных вызовов. При определении среднего числа повторных вызовов  , приходящихся на один первичный вызов, следует учитывать, что появление повторных вызовов от источника вызвано как отсутствием свободных линий на выходе коммутационной схемы, так и только первым этапом обслуживания вызова. Отсюда
, приходящихся на один первичный вызов, следует учитывать, что появление повторных вызовов от источника вызвано как отсутствием свободных линий на выходе коммутационной схемы, так и только первым этапом обслуживания вызова. Отсюда
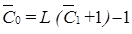 , (7.3)
, (7.3)
где  - среднее число попыток на первом этапе добиться полного обслуживания вызова;
- среднее число попыток на первом этапе добиться полного обслуживания вызова;  - среднее число повторных вызовов, приходящих на один первичный и повторный вызовы, которые возникают из-за отсутствия свободных линий на выходе коммутационной системы.
- среднее число повторных вызовов, приходящих на один первичный и повторный вызовы, которые возникают из-за отсутствия свободных линий на выходе коммутационной системы.
|
|
|
Величина  может быть найдена из выражения
может быть найдена из выражения
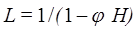 . (7.4)
. (7.4)
Для определения  и
и  используются таблицы [6], в которых значения этих величин приведены в зависимости от емкости пучка линий V на выходе коммутационной системы при фиксированных значениях
используются таблицы [6], в которых значения этих величин приведены в зависимости от емкости пучка линий V на выходе коммутационной системы при фиксированных значениях
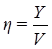 ,
, 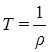 и
и 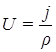 . (7.5)
. (7.5)
Значения 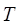 и
и  могут быть найдены из следующих выражений:
могут быть найдены из следующих выражений:
 ;
; 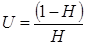 . (7.6)
. (7.6)
Величину 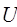 можно рассматривать как меру «ненастойчивости» абонента. Так, если абонент абсолютно настойчив Н =1, а U =0.
можно рассматривать как меру «ненастойчивости» абонента. Так, если абонент абсолютно настойчив Н =1, а U =0.
В таблице П.1 приложения приведены значения 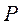 и
и  в виде мантиссы и порядка для V =12 – 60 при
в виде мантиссы и порядка для V =12 – 60 при 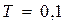 и
и 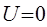 , V =12-50 при T =0,2 и U =0,5
, V =12-50 при T =0,2 и U =0,5
Задание 7.
1.Построить зависимость вероятности потерь первичных вызовов  и среднего числа повторных вызовов
и среднего числа повторных вызовов 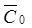 , приходящихся на один первичный вызов, от среднего использования линий
, приходящихся на один первичный вызов, от среднего использования линий  на выходе однозвенной полнодоступной коммутационной схемы по направлению к узлу специальных служб (УСС) для вероятностей поступления повторных вызовов
на выходе однозвенной полнодоступной коммутационной схемы по направлению к узлу специальных служб (УСС) для вероятностей поступления повторных вызовов 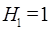 и
и 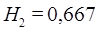 . При определении
. При определении 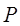 и
и 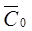 принять
принять 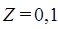 ч. Результаты расчета представить в виде графиков
ч. Результаты расчета представить в виде графиков 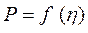 и
и 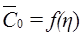 для
для 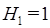 и
и 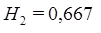 и таблицы 7.1.
и таблицы 7.1.
Таблица 7.1
| № пп | Y | 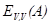
| 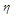
| H=1 | H=0,667 | ||||
| P | 
| 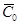
| P | 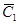
| 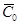
| ||||
| . | |||||||||
| . | |||||||||
| 5. |
На графике  привести зависимость
привести зависимость 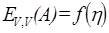 и сравнить значение
и сравнить значение 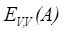 и
и 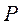 по величине. Объяснить полученные зависимости.
по величине. Объяснить полученные зависимости.
Примечание. Диапазон нагрузок к УСС (не менее пяти точек) взять из таблицы 4.3 задания 4 так, чтобы 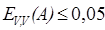 .
.
2.Подобрать такое число линий в направлении к УСС, чтобы с учетом повторных вызовов потери первичных вызовов не превышали заданную норму  .
.
Тема 8. Методы расчета пропускной способности однозвенных неполнодоступных включений: упрощенная формула Эрланга, формула О’Делла, формула Пальма-Якобеуса
Для практических расчетов пропускной способности однозвенных неполнодоступных включений (рис.8.1) используются приближенные методы.
Упрощенная формула Эрланга:
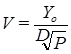 , (8.1)
, (8.1)
где 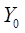 - интенсивность обслуженной пучком линий нагрузки;
- интенсивность обслуженной пучком линий нагрузки; 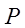 - вероятность потерь;
- вероятность потерь; 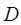 - доступность;
- доступность;  - средняя пропускная способность одной линии пучка. Эта формула дает грубую приближенную оценку пропускной способности неполнодоступного включения (завышается пропускная способность НПД пучка).
- средняя пропускная способность одной линии пучка. Эта формула дает грубую приближенную оценку пропускной способности неполнодоступного включения (завышается пропускная способность НПД пучка).
|
|
|
 |
Рис.8.1. Неполнодоступное (НПД) включение линий
а) схема запараллеливания выходов; б) условное изображение НПД схемы.
Формула О’Делла:
 , (8.2)
, (8.2)
где 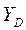 - нагрузка, обслуженная полнодоступным пучком из
- нагрузка, обслуженная полнодоступным пучком из 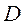 линий при потерях
линий при потерях 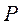 и приблизительно определяемая с помощью 1-ой формулы Эрланга (по таблицам Пальма).
и приблизительно определяемая с помощью 1-ой формулы Эрланга (по таблицам Пальма).
Формула Пальма – Якобеуса:
 (8.3)
(8.3)
где А – интенсивность поступающей на пучок линий нагрузки.
При малых значениях потерь  можно считать
можно считать  . Поэтому все эти формулы при фиксированных
. Поэтому все эти формулы при фиксированных 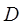 и
и 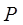 могут быть приведены к виду:
могут быть приведены к виду:
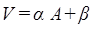 , (8.4)
, (8.4)
где значения  и
и 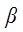 зависят от
зависят от  и
и 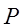 .
.
Для упрощенной формулы Эрланга:
 ,
, 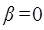 ; (8.5)
; (8.5)
Для формулы О’Делла:
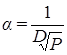 ,
, 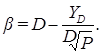 (8.6)
(8.6)
Для формулы Пальма – Якобеуса эти коэффициенты можно подобрать. Значения  и
и 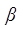 для формулы О’Делла табулированы и для некоторых значений
для формулы О’Делла табулированы и для некоторых значений  и
и 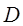 приведены в таблице П.4 Приложения.
приведены в таблице П.4 Приложения.
Задание 8.
1.Рассчитать и построить зависимости числа линий V и коэффициента среднего использования 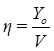 от интенсивности поступающей нагрузки А при величине потерь
от интенсивности поступающей нагрузки А при величине потерь 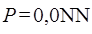 , где NN – двухзначный номер варианта, и значениях доступности
, где NN – двухзначный номер варианта, и значениях доступности  , используя метод О’Делла. Результаты расчета представить в виде таблицы 8.1 и графика. Значения А соответствуют нагрузкам на направлениях, рассчитанным при выполнении задания 3 (таблица 3.1). Следить, чтобы выполнялось условие НПД включения V>D.
, используя метод О’Делла. Результаты расчета представить в виде таблицы 8.1 и графика. Значения А соответствуют нагрузкам на направлениях, рассчитанным при выполнении задания 3 (таблица 3.1). Следить, чтобы выполнялось условие НПД включения V>D.
2. Рассчитать и построить зависимость числа линий  от величины потерь
от величины потерь 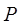 неполнодоступного пучка при значении
неполнодоступного пучка при значении 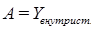 и
и 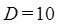 по формуле Эрланга, О’Делла, Пальма – Якобеуса. Результаты расчета представить в виде таблицы 8.2 и графика.
по формуле Эрланга, О’Делла, Пальма – Якобеуса. Результаты расчета представить в виде таблицы 8.2 и графика.
Таблица 8.1.
| Направление связи от АТСЭ-4 | А, Эрл | 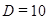
| 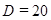
| 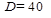
| |||
| V | 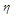
| V | 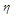
| V | 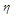
| ||
| УСС | |||||||
| АМТС | |||||||
| ЦПС | |||||||
| IP-сеть | |||||||
| АТСЭ – 1 | |||||||
| АТСДШ – 2 | |||||||
| АТСК – 3 | |||||||
| АТСЭ – 4 (внутристанционное) |
|
|
|
Таблица 8.2.
| № п.п. | 
| 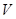 , рассчитанное по формулам , рассчитанное по формулам
| ||
| Эрланга | О’ Делла | Пальма –Якобеуса | ||
| . . . | 0,001 0,005 0,01 . . . 0,2 |
Тема 9. Метод Якобеуса для расчета пропускной способности двухзвенных полнодоступных включений
Многозвенные коммутационные схемы имеют значительно большее число состояний, чем однозвенные. Поэтому система уравнений для вероятностей состояний многозвенной коммутационной схемы не только не может быть решена, но и во многих случаях не может быть записана.
Поэтому для расчета двухзвенных коммутационных схем при полнодоступном включении линий применяется приближенный комбинаторный метод Якобеуса.
Вызов в двухзвенной схеме может быть потерян в одном из трех случаев:
1) если заняты все промежуточные линии, которые могут быть использованы для обслуживания этого вызова;
2) если заняты все выходы в требуемом направлении;
3) если возникают неудачные комбинации свободных промежуточных линий и свободных выходов.
Вид формулы Якобеуса для вероятности потерь в двухзвенной коммутационной схеме при полнодоступном включении линий зависит от соотношения основных коммутационных параметров блока искания,
определяющих применение закона распределения вероятностей занятия обслуживающих устройств на первом и втором звеньях.
Примем следующие обозначения: 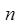 - число входов в каждый коммутатор звена А;
- число входов в каждый коммутатор звена А; 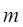 - число выходов из каждого коммутатора звена А;
- число выходов из каждого коммутатора звена А;  - коэффициент сжатия или расширения,
- коэффициент сжатия или расширения, 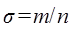 ;
; 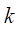 - число коммутаторов на звене А;
- число коммутаторов на звене А; 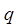 - число выходов, выделяемых в направлении искания из каждого коммутатора звена В;
- число выходов, выделяемых в направлении искания из каждого коммутатора звена В; 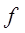 -связность блока;
-связность блока; 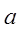 - нагрузка на один вход;
- нагрузка на один вход; 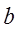 - нагрузка на одну промежуточную линию блока;
- нагрузка на одну промежуточную линию блока; 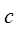 - нагрузка на один выход в направлении искания;
- нагрузка на один выход в направлении искания;  - интенсивность поступающей нагрузки в данном направлении (рис.9.1).
- интенсивность поступающей нагрузки в данном направлении (рис.9.1).
 |
Рис.9.1. Двухзвенное полнодоступное блокируемое включение V=mq.
Если  , то на первом звене А применяют распределение Бернулли, на втором звене – распределение Эрланга. Расчетные формулы для вероятности потерь
, то на первом звене А применяют распределение Бернулли, на втором звене – распределение Эрланга. Расчетные формулы для вероятности потерь  следующие:
следующие:
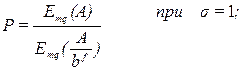 (9.1)
(9.1)
 (9.2)
(9.2)
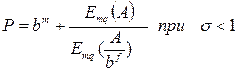 (9.3)
(9.3)
Если  , то на звеньях А и В используется распределение Бернулли. Расчетные формулы следующие:
, то на звеньях А и В используется распределение Бернулли. Расчетные формулы следующие:
 (9.4)
(9.4)
(9.5)
(9.6)
Если величина потерь  задана, то число линий V=mq из приведенных уравнений определяется путем подбора такого значения
задана, то число линий V=mq из приведенных уравнений определяется путем подбора такого значения 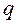 , при котором
, при котором 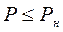 .
.
Задание 9.
1. Для заданного в таблице 6.2. задания 6 двухзвенного блока ГИ построить схему группообразования в координатном виде и рассчитать величину вероятности потерь для направлений к УСС и АМТС при полнодоступном двухзвенном включении линий. Значения интенсивности нагрузок в направлениях к АМТС и УСС взять из результатов расчета задания 3.
|
|
|
2. Для того же двухзвенного блока ГИ найти необходимое число линий в направлении от АТСК-3 к проектируемой АТСЭ-4, предполагая полнодоступное включение, при потерях 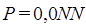 , где
, где 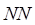 - двухзначный номер варианта.
- двухзначный номер варианта.
Значение интенсивности нагрузки в направлении взять из результатов расчета задания 3. Нагрузку на один вход блока взять из задания 6.
Тема 10. Методы расчета пропускной способности двухзвенных схем, в выходы которых включен неполнодоступный пучок линий
Метод Якобеуса
Неполнодоступное включение линий имеет место при условии 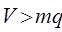 . Это включение аналогично рис.9.1, но на ПЩ выполняется НПД включение
. Это включение аналогично рис.9.1, но на ПЩ выполняется НПД включение  .
.
|
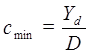 (
(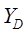 - определяется по 1-ой формуле Эрланга) и максимальным значением
- определяется по 1-ой формуле Эрланга) и максимальным значением 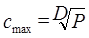 .
.
Величина 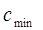 определяется для случая
определяется для случая  .
.
В соответствии с идеей О’Делла число линий неполнодоступного пучка может быть определено из выражения:
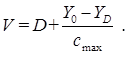 (10.1)
(10.1)
Для двухзвенных схем 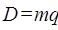 и
и 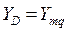 . Для определения
. Для определения 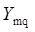 можно воспользоваться соответствующими уравнениями Якобеуса, полученными для двухзвенных схем, в выходы которых включен полнодоступный пучок линий. Например, для
можно воспользоваться соответствующими уравнениями Якобеуса, полученными для двухзвенных схем, в выходы которых включен полнодоступный пучок линий. Например, для 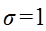 и
и 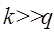 ,
, 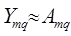 можно определить из уравнения
можно определить из уравнения
 (10.2)
(10.2)
путем подбора при известных 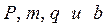 .
.
При определении 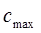 предполагается очень большое число линий
предполагается очень большое число линий  и для нахождения
и для нахождения  при
при 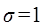 следует воспользоваться формулой Якобеуса для полнодоступного включения, полученной в предположении распределения Бернулли на первом и втором звеньях:
следует воспользоваться формулой Якобеуса для полнодоступного включения, полученной в предположении распределения Бернулли на первом и втором звеньях:
 . (10.3)
. (10.3)
Таким образом, для  необходимо решить систему уравнений:
необходимо решить систему уравнений:
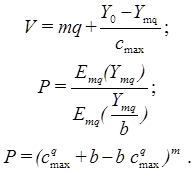 (10.4)
(10.4)
Аналогичным образом получены уравнения для коммутационных двухзвенных схем с расширением и со сжатием:
Для 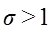

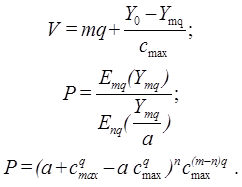 (10.5)
(10.5)
Для 
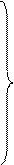
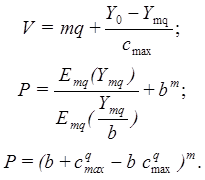 (10.6)
(10.6)
При малой величине потерь 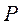 в (10.4) – (10.6) обычно принимается
в (10.4) – (10.6) обычно принимается 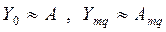 .
.
Порядок решения системы уравнений Якобеуса при определении необходимого числа линий при заданных значениях нагрузки А и качестве обслуживания P следующий:
1)методом подбора с использованием таблиц Пальма [4,8] из второго уравнения системы определяется 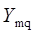 ;
;
2)методом подбора (или решением) из третьего уравнения системы находится 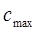 ;
;
3)подставляя полученные значения 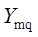 и
и 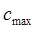 в первое уравнение, определяется число линий
в первое уравнение, определяется число линий  .
.
|
|
|



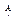 А
А