 |
Определение оптимального числа линий в прямом направлении
|
|
|
|
Оптимальное число линий в прямом направлении зависит от интенсивности нагрузки, поступающей на прямое направление ij 
;
отношения затрат на одну линию в прямом направлении к затратам на одну линию в обходном направлении 
; величины потерь, при которой рассчитывается количество линий в обходном направлении - 
.
Число линий в прямом направлении 
будем считать оптимальным, если выполняются следующие условия:
1) экономия от уменьшения числа линий в прямом направлении на одну от оптимального не превышает затрат на организацию дополнительного числа линий в обходном направлении, необходимых для обслуживания дополнительной нагрузки, поступающей на обходное направление при уменьшении числа линий в прямом направлении на одну;
2) затраты на организацию дополнительной линии в прямом направлении больше экономии от соответствующего уменьшения числа линий на обходном направлении.
При полнодоступном неблокируемом включении линий МСЭ-Т рекомендуется (Рекомендация Е.522) использовать следующее условие оптимальности:
, (13.1)
где 
- первая формула Эрланга; М – увеличение пропускной способности пучка линий обходного направления при добавлении к этому пучку одной линии.
Оптимальное число линий по условию (13.1) определяется путем последовательных приближений. Эти расчеты относительно трудоемки. Поэтому для начала подбора можно воспользоваться приближенным методом определения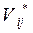 
. Как показали исследования, зависимость 
при 
и 
достаточно хорошо описывается уравнением прямой 
. Значения коэффициентов а и в при 
для различных 
приведены в табл. 13.1.
Таблица 13.1
| 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
| а | 1,162 | 1,143 | 1,132 | 1,128 | 1,124 | 1,120 |
 в
| 2,0 | 1,5 | 0,9 | -0,8 | -2,4 | -0,5 |
|
|
|
13.3. Расчета числа линий при обслуживании вызовов избыточной нагрузки
Для характеристики избыточной нагрузки используют два параметра: математическое ожидание 
и пикфактор (коэффициент скученности) 
, определяемый отношением дисперсии нагрузки к ее математическому ожиданию: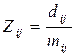 
.
Для простейшего потока вызовов значение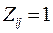 
, для избыточного потока Zij >1.
Математическое ожидание и дисперсию избыточной нагрузки можно найти из следующих выражений:
. (13.2)
В общем случае на обходное направление могут поступать избыточные нагрузки от нескольких прямых направлений. Если принять, что поступающие на прямые направления нагрузки являются независимыми, то избыточные нагрузки будут также независимыми, и параметры объединенной на обходном направлении нагрузки определяются из выражения:
(13.3)
Определить число линий в обходном направлении можно с помощью метода Вилкинсона, являющегося одним из вариантов метода эквивалентных замен.
Сущность метода заключается в замене схемы включения рис. 13.2а на схему рис.13.2б, называемую эквивалентной схемой. В эквивалентной схеме предполагается, что избыточная нагрузка 
получена при обслуживании поступающей нагрузки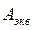 
- линейным пучком.
а) б)
Рис.13.2. Реальная и эквивалентная схемы включения линий на обходном направлении
Зная значения 
и 
, находят число линий 
и нагрузку 
, решая систему уравнений методом подбора:
(13.4)
Затем также подбором по заданной норме величины потерь 
в обходном направлении определяют 
из уравнения с помощью таблиц Пальма:
(13.5)
Процесс подбора 
и 
из уравнения (13.4) трудоемок, поэтому можно воспользоваться приближенными выражениями, полученными Раппом:
(13.6)
Порядок расчета линий в обходном направлении методом Вилкинсона следующий:
1) по (13.2) для каждого прямого направления ij рассчитываются mij и dij;
2) по (13.3) определяются значения математического ожидания и дисперсии избыточных нагрузок, не обслуженных в прямых направлениях - 
|
|
|
3) по (13.6) находятся значения 
и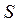 
эквивалентной схемы;
4) рассчитывается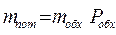 
;
5) рассчитывается 
;
6) с помощью таблиц Пальма по значениям 
и 
определяется 
;
7) рассчитывается число линий в обходном направлении
.
Задание 13.
1.Рассчитать оптимальное число линий в прямых направления от проектируемой АТСЭ-4 к АТСДШ-2 иАТСК-3. В качестве обходной принять АТСЭ-1.
2.Рассчитать параметры избыточной нагрузки от прямых направлений 4-2 и 4-3.
3.Построить реальную и эквивалентную схемы включения линий на обходном направлении и рассчитать число линий на этом направлении при норме величины потерь 
.
Для расчетов воспользоваться следующими исходными данными:
1) интенсивность нагрузки в прямых направлениях принять в соответствии с заданием 3;
2) для определения расстояния составить матрицу расстояний между АТС в соответствии с заданием 3;
3) значение затрат на организацию одной соединительной линии принять в соответствии с таблицей 13.2; затраты на один вход коммутационного оборудования принять 1500 руб.
Таблица 13.2
| Диапазон расстояний | Затраты на 1 км линии, руб. |
| от 0 до 5 от 5 до 10 от 10 до 13 свыше 13 |
4) нагрузку на обоих участках обходного направления принять одинаковой и равной нагрузке от проектируемой АТСЭ-4 к АТСЭ-1 
;
5)сравнить по суммарным капитальным затратам варианты организации связи (рис.13.1).
Литература
1. Корнышев Ю.Н., Пшеничников А.П., Харкевич А.Д. Теория телетрафика. - М: Радио и связь, 1996. 224с.
2. Шнепс М.А. Системы распределения информации. Методы расчета. - М.: Связь, 1979. 342с.
3. Корнышев Ю.Н., Фань Г.Л. Теория распределения информации. - М.: Радио и связь, 1985. 184с.
4. Башарин Г.П. Таблицы вероятностей и средних квадратичных отклонений потерь на полнодоступном пучке линий. - М.: АН СССР, 1962. - 128с.
5. Лившиц Б.С., Фидлин Я.В. Системы массового обслуживания с конечным числом источников. -М.: Связь, 1968. - 167с.
6. Ионин Г.Л., Седол Я.Я. Таблицы вероятностных характеристик полнодоступного пучка при повторных вызовах. - М.: Наука, 1970. - 155с.
7. Захаров Г.П., Варакосин Н.П. Расчет количества каналов связи при обслуживании с ожиданием. - М.: Связь, 1967. - 194с.
|
|
|
8. Мамонтова Н.П. Теория телетрафика. Методические рекомендации к изучению дисциплины 20900. Санкт-Петербургский государственный университет телекоммуникаций им. Проф. М.А. Бонч-Бруевича.(http://dvo.sut.ru/libr/skiri/w169mamo/index.htm)
Приложение
Таблица П.1 Значения вероятности потерь первичных вызовов Р и среднего числа повторных вызовов 
Т = 0,1 U = 0
| V = 12 | V = 14 | V = 16 | V = 18 | ||||
|
| P |
| P |
| P |
| P | |
| 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 | 8774-6 1640-4 1427-3 7680-3 2983-2 9171-2 2371-1 5375-1 1103-0 2097-0 3970-0 6521-0 1105+1 1871+1 3264+1 6212+1 | 4361-6 7852-5 6553-4 3373-3 1247-2 3629-2 8827-2 1869-1 3548-1 6173-1 1001-0 1533-0 2241-0 3154-0 4305-0 5739-0 | 9233-7 2762-5 3379-4 2358-3 1122-2 4054-2 1194-1 3010-1 6736-1 1375-0 2622-0 4762-0 8500-0 1471+1 2639+1 5142+1 | 4944-7 1428-5 1681-4 1125-3 5108-3 1753-2 4873-2 1151-1 2391-1 4484-1 7741-1 1250-0 1910-0 2793-0 3941-0 5414-0 | 9980-8 4780-6 8224-5 7438-4 4337-3 1843-2 6188-2 1735-1 4233-1 9278-1 1875-0 3572-0 6553-0 1186+1 2185+1 4354+1 | 5668-8 2628-6 4364-5 3795-4 2118-3 8570-3 2723-2 7173-2 1630-1 3292-1 6044-1 1027-0 1640-0 2488-0 3625-0 5123+0 | 8428-7 2042-5 2396-4 1713-3 8563-3 3277-2 1022-1 2718-1 6395-1 1369-0 2734-0 5215-0 9739-0 1842+1 3751+1 | 4879-7 1143-5 1292-4 8862-4 4230-3 1536-2 4512-2 1121-1 2438-1 4757-1 8504-1 1416-0 2227-0 3347-0 4860-0 |
|
| V = 20 | V = 22 | V = 24 | V = 26 | ||||
|
| Р |
| Р |
| Р |
| Р | |
| 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 | 5147-6 7839-5 6873-4 4045-3 1765-2 6222-2 1776-1 4484-1 1017-0 2128-0 4216-0 8123-0 1576+1 3276+1 | 3014-6 4432-5 3737-4 2104-3 8730-3 2860-2 7772-2 1818-1 3769-1 7083-1 1230-0 2003-0 3101-0 4621-0 | 1304-6 2583-5 2489-4 1936-3 9635-3 3718-2 1177-1 3188-1 7654-1 1678-0 3453-0 6860-0 1364+1 2894+1 | 7991-7 1528-5 1585-4 1053-3 4994-3 1824-2 5419-2 1364-1 3002-1 5930-1 1073-0 1808-0 2881-0 4402-0 | 3362-7 8650-6 1148-4 9367-4 5320-3 2285-2 7885-2 2293-1 5829-1 1339-0 2859-0 5853-0 1193+1 2580+1 | 2130-7 5300-6 6757-5 5294-4 2871-3 1670-2 3799-2 1029-1 2404-1 4986-1 9390-1 1637-0 2683-0 4201-0 | 8806-8 2937-6 4762-5 4575-4 2962-3 1417-2 5335-2 1664-1 4481-1 1078-0 2388-0 5038-0 1051+1 2318+1 | 5705-8 1847-6 2894-5 2675-4 1658-3 7535-3 2675-2 7790-2 1932-1 4208-1 8249-1 1486-0 2504-0 4015-0 |
|
| V = 28 | V = 30 | V = 32 | V = 34 | ||||
|
| P |
| P |
| P |
| P | |
| 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 | 9990-7 1989-5 2251-4 1664-3 8857-3 3639-2 1218-1 3473-1 8745-1 2011-0 4369-0 9335-0 2097+1 | 6453-7 1244-5 1356-4 9615-4 4872-3 1891-2 5923-1 1559-1 3564-1 7268-1 1353-0 2342-0 3843-0 | 3418-7 8357-6 1115-4 9409-4 5575-3 2500-2 8983-2 2711-1 7147-1 1705-0 3813-0 8339-0 1908+1 | 2262-7 5361-6 6901-5 5593-4 3161-3 1341-2 4518-2 1262-1 3027-1 6421-1 1234-0 2194-0 3683-0 | 1159-7 3436-6 5432-5 5338-4 3529-3 1727-2 6663-2 2129-1 5876-1 1454-0 3347-0 7490-0 1745+1 | 7937-8 2308-6 3508-5 3262-4 2057-3 9543-3 3457-2 1024-1 2578-1 5687-1 1128-0 2059-0 3533-0 | 4006-8 1460-6 2751-5 3054-4 2247-3 1200-2 4969-2 1681-1 4857-1 1246-0 2953-0 6760-0 1603+1 | 2796-8 1000-6 1798-5 1909-4 1342-3 6807-3 2652-2 8337-2 2201-1 5047-1 1033-0 1935-0 3393-0 |
|
|
|
Т = 0,1 U = 0 Продолжение табл. П.1
|
| V = 36 | V = 38 | V = 40 | V = 42 | ||||
|
| Р |
| Р |
| Р |
| Р | |
| 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 | 6225-7 1390-5 1754-4 1436-3 8374-3 3723-2 1334-1 4034-1 1073-0 2617-0 6126-0 1479+1 | 4345-7 9226-6 1119-4 8739-4 4868-3 2039-2 6801-2 1884-1 4488-1 9479-1 1821-0 3261-0 | 2664-7 7012-6 1011-4 9220-4 5868-3 2802-2 1063-1 3365-1 9284-1 2329-0 5574-0 1369+1 | 1891-7 4739-6 6574-5 5753-4 3488-3 1571-2 5559-2 1615-1 3999-1 8711-1 1716-0 3138-0 | 1144-7 3549-6 5839-5 5939-4 4128-3 2116-2 8502-2 2817-1 8059-1 2080-0 5088-0 1271+1 | 8244-8 2439-6 3869-5 3779-4 2504-3 1213-2 4553-2 1387-1 3569-1 8016-1 1619-0 3021-0 | 5048-8 1808-6 3390-5 3839-4 2908-3 1603-2 6824-2 2367-1 7020-1 1863-0 4660-0 1184+1 | 3613-8 1258-6 2281-5 2485-4 1801-3 9385-3 3736-2 1194-1 3190-1 7386-1 1529-0 2911-0 |
|
| V = 44 | V = 46 | V = 48 | V = 50 | ||||
|
| P |
| P |
| P |
| P | |
| 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 | 9201-7 1971-5 2488-4 2061-3 1290-2 5494-2 1995-1 6134-1 | 6492-7 1347-5 1637-4 1297-3 7271-3 3070-2 1029-1 2855-1 | 4694-7 1149-5 1617-4 1463-3 9292-3 4436-2 1686-1 5375-1 | 3356-7 7965-6 1080-4 9359-4 5641-3 2527-2 8876-2 2559-1 | 2400-7 6716-6 1053-4 1041-3 7101-3 3591-2 129-1 4722-1 | 1737-7 4715-6 7135-5 6761-4 4383-3 2082-2 7670-2 2296-1 | 1229-7 3932-6 6871-5 7422-4 5439-3 2914-2 1214-1 4158-1 | 8997-8 2795-6 4719-5 4890-4 3410-3 1718-2 6636-2 2063-1 |
Т = 0,1 U = 0 Т = 0,2 U = 0,5
|
| V = 55 | V = 60 | V = 55 | V = 60 | ||||
|
| Р |
| Р |
| Р |
| Р | |
| 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 | 9739-7 2254-5 3191-4 2817-3 1743-2 8148-2 3053- 9716-1 2792-0 7881-0 | 7499-7 1665-5 2183-4 1829-3 1068-2 4643-2 1585-1 4459-1 1077-0 2324-0 | 2605-7 8117-6 1403-4 1476-3 1055-2 5532-2 2268-1 7734-1 2342-0 6875-0 | 2050-7 6024-6 9829-5 9871-4 6681-3 3792-2 1226-1 3709-1 9489-1 2143-0 | 5095-7 1092-5 1434-4 1156-3 6402-3 2587-2 8012-2 1984-1 4082-1 7227-1 | 6809-7 1462-5 1830-4 1453-3 7926-3 3152-2 9589-2 2330-1 4692-1 8136-1 | 1386-7 4016-6 6452-5 6245-4 4014-3 1829-2 6224-2 1657-1 3598-1 6622-1 | 1873-7 5315-6 8311-5 7935-4 5027-3 2254-2 7537-2 1969-1 4188-1 7540-1 |
Т = 0,5 U = 0,5 Продолжение табл. П.1
|
| V = 12 | V = 14 | V = 16 | V = 18 | ||||
|
| P |
| P |
| P |
| P | |
| 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 | 3842-6 6844-5 5631-4 2845-3 1028-2 2907-2 6826-2 1386-1 2507-1 4126-1 6287-1 8992-1 1220-0 1585-0 1985-0 2412-0 2857-0 | 4155-6 7318-5 5953-4 2972-3 1061-2 2963-2 6870-2 1377-1 2458-1 3992-1 6003-1 8471-1 1134-0 1453-0 1796-0 2154-0 2517-0 | 235-6 1212-5 1409-4 9273-4 4124-3 1378-2 3708-2 8413-2 1666-1 2954-1 4785-1 7193-1 1016-0 1364-0 1755-0 2179-0 2627-0 | 4731-7 3126-5 3023-4 1001-3 4399-3 1452-2 3854-2 8630-2 1686-1 2949-1 4710-1 6979-1 9722-1 1286-0 1631-0 1996-0 2372-0 | 4734-8 2182-6 3583-5 3070-4 1681-3 6638-3 2045-2 5182-2 1124-1 2147-1 3695-1 5834-1 8579-1 1189-0 1570-0 1990-0 2438-0 | 5442-8 2477-6 4022-5 3406-4 1843-3 7184-3 2184-2 5462-2 1168-1 2200-1 3731-1 5805-1 8409-1 1148-0 1493-0 1863-0 2249-0 | 3977-7 9224-6 1775-4 6935-4 3235-3 1141-2 4086-2 7669-2 1578-1 2884-1 4783-1 7316-1 1047-0 1417-0 1832-0 2281-0 | 4617-7 1059-5 1993-4 7779-4 3583-3 1247-2 4358-2 8154-2 1653-1 2978-1 4864-1 7325-1 1032-0 1374-0 1749-0 2143-0 |
|
| V = 20 | V = 22 | V = 24 | V = 26 | ||||
|
| Р |
| Р |
| Р |
| Р | |
| 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 | 2398-6 3482-5 2888-4 1519-3 6424-3 2031-2 5280-2 1170-1 2271-1 3955-1 6290-1 9283-1 1288-0 1698-0 2146-0 | 2808-6 4032-5 3305-4 1799-3 7166-3 2235-2 5728-2 1250-1 2391-1 4099-1 6417-1 9318-1 1272-0 1649-0 2050-0 | 6271-7 1187-5 1212-4 7888-4 3645-3 1287-2 3663-2 8738-2 1802-1 3293-1 5446-1 8287-1 1178-0 1582-0 2030-0 | 7479-7 1399-5 1411-4 9073-4 4239-3 1442-2 4044-2 9505-2 1930-1 3472-1 5648-1 8454-1 1181-0 1560-0 1967-0 | 1653-7 4074-6 5119-5 3936-4 2082-3 8209-3 2557-2 6567-2 1438-1 2759-1 4741-1 7439-1 1083-0 1482-0 1928-0 | 2001-7 4874-6 6053-5 4597-4 2400-3 9339-3 2868-2 7256-2 1564-1 2953-1 4992-1 1699-1 1101-0 1481-0 1893-0 | 4390-8 1407-6 2175-5 1973-4 1195-3 5262-3 1794-2 4961-2 1154-1 2322-1 4148-1 6707-1 9994-1 1393-0 1838-0 | 5374-8 1705-6 2606-5 2338-4 1397-3 6071-3 2041-2 5559-2 1273-1 25-1-1 4426-1 7035-1 1030-0 1409-0 1826-0 |
|
| V = 28 | V = 30 | V = 32 | V = 34 | ||||
|
| Р |
| Р |
| Р |
| Р | |
| 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 | 4878-7 9275-6 9946-5 6892-4 3389-3 1264-2 3764-2 9293-2 1964-1 3644-1 6072-1 9260-1 1314-0 1757-0 | 5980-7 1125-5 1193-4 8160-4 3959-3 1457-2 4272-2 1038-1 2158-1 3937-1 6446-1 9653-1 1344-0 1764-0 | 1698-7 3973-6 5031-5 3990-4 2191-3 8945-3 3283-2 7516-2 1808-1 3213-1 5516-1 8608-1 1243-0 1684-0 | 2103-7 4872-6 6009-5 4778-4 2589-3 1042-2 3291-2 8494-2 1853-1 3511-1 5920-1 9070-1 1285-0 1708-0 | 5904-8 1694-6 2519-5 2313-4 1420-3 6349-3 2191-2 6098-2 1419-1 2842-1 5026-1 8024-1 1179-0 1618-0 | 7414-8 2113-6 3132-5 2803-4 1697-3 7478-3 2542-2 6966-2 1564-1 3137-1 5450-1 8539-1 1230-0 1656-0 | 2068-8 7303-7 1295-5 1350-4 9243-4 4521-3 1679-2 4962-2 1211-1 2520-1 4592-1 7499-1 1120-0 1558-0 | 2620-8 9192-7 1606-5 1649-4 1114-3 5376-3 1968-2 5724-2 1374-1 2810-1 5026-1 8054-1 1180-0 1608-0 |
|
|
|
Т = 0,5 U = 0,5 Продолжение табл. П.1
|
| V = 36 | V = 38 | V = 40 | V = 42 | ||||
|
| Р |
| Р |
| Р |
| Р | |
| 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 | 3156-7 6632-6 7891-5 6029-4 3227-3 1290-2 4048-2 1037-1 2241-1 4205-1 7024-1 1067-0 1502-0 | 4006-7 8271-6 9719-5 7333-4 3872-3 1526-2 4712-2 1187-1 2521-1 4644-1 7609-1 1133-0 1563-0 | 1367-7 3393-6 4621-5 3942-4 2309-3 9938-3 3310-2 8896-2 1997-1 3869-1 6592-1 1019-0 1451-0 | 1749-7 4265-6 5737-5 4833-4 2739-3 1185-2 3886-2 1027-1 2265-1 4297-1 7198-1 1090-0 1522-0 | 5935-8 1740-6 2712-5 2583-4 1656-3 7671-3 2713-2 7649-2 1783-1 3549-1 6198-1 9734-1 1404-0 | 7644-8 2203-6 3392-5 3191-4 2018-3 9217-3 3209-2 8900-2 2039-1 3982-1 6819-1 1049-0 1482-0 | 2606-8 8954-7 1595-5 1695-4 1189-3 5932-3 2227-2 6588-2 1596-1 3269-1 5837-1 9319-1 1260-0 | 3349-8 1139-6 2008-5 2109-4 1460-3 7179-3 2654-2 5684-2 1837-1 3695-1 6468-1 1012-0 1446-0 |
|
| V = 44 | V = 46 | V = 48 | V = 50 | ||||
|
| Р |
| Р |
| Р |
| Р | |
| 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 | 4608-7 9396-6 1115-4 8560-4 4595-3 1831-2 5684-2 1430-1 3017-1 5506-1 8934-1 1320-0 | 5900-7 1190-5 1396-4 1058-3 5599-3 2198-2 6709-2 1658-1 3433-1 6142-1 9760-1 1411-0 | 2376-7 5543-6 7344-5 6171-4 3565-3 1508-2 4912-2 1283-1 2788-1 5201-1 8575-1 1281-0 | 3058-7 7063-6 9252-5 7673-4 4372-3 1822-2 5835-2 1498-1 3192-1 5838-1 9426-1 1378-0 | 1226-7 3274-6 4845-5 4554-4 2770-3 1244-2 4250-2 1153-1 2579-1 4918-1 8241-1 1246-0 | 1587-7 4196-6 6137-5 5571-4 3417-3 1512-2 5081-2 1354-1 2972-1 5554-1 9111-1 1347-0 | 6339-8 1936-6 3200-5 3220-4 2155-3 1028-2 3683-2 1038-1 2690-1 4657-1 7928-1 1212-0 | 8244-8 2495-6 4075-5 4049-4 2673-3 1256-2 4428-2 1226-1 2769-1 5289-1 8813-1 1318-0 |
Примечание: число8774-6 означает 0,8774·10-6
число 6212+1 означает 0,6212·101
Таблица П.2
Трехшаговые схемы цилиндров
| Число групп | Параметры схемы | Первая строка матрицы | Число групп | Параметры схемы | Первая строка матрицы |
| [1,2] [1,1] [1,2] [1,1] [1,2] [2,2] [1,2] [1,2] [1,3] [2,2] [1,2] [1,3] [1,4] [2,3] [1,2] [1,3] [1,4] [2,2] [2,3] [1,2] [1,3] [1,4] [2,3] [2,4] [1,2] [1,3] [1,4] [1,5] [2,3] [2,4] [3,4] | [1,2] [1,3] [1,4] [1,5] [2,3] [2,4] [2,5] [3,4] [1,2] [1,3] [1,4] [1,5] [1,6] [2,3] [2,4] [2,5] [3,4] [3,5] [1,2] [1,3] [1,4] [1,5] [1,6] [2,3] [2,4] [2,5] [2,6] [3,4] [3,5] [4,5] |
Пример трехшагового цилиндра Матрица связности
 |
Таблица П.3
Четырехшаговые схемы цилиндров
| Число групп | Параметры схемы | Первая строка матрицы | Число групп | Параметры схемы | Первая строка матрицы |
| [1,1,2] [1,1,1] [1,1,2] [1,2,1] [1,2,2] [1,1,2] [1,1,1] [1,2,1] [1,2,2] [1,1,2] [1,1,3] [1,2,2] [1,2,3] [1,3,1] [1,1,2] [1,1,3] [1,2,1] [1,2,2] [1,2,4] [1,3,2] [1,1,2] [1,1,3] [1,2,1] [1,2,2] [1,2,3] [1,2,4] [1,3,2] [1,4,1] [2,3,2] | [1,1,3] [1,2,2] [1,2,4] [1,2,5] [1,3,2] [1,1,3] [1,2,2] [1,2,1] [1,2,5] [1,3,5] [1,5,1] [2,4,2] [1,2,6] [1,3,2] [1,2,4] [1,2,5] [1,2,7] [1,3,2] [1,4,2] [1,4,3] [2,4,3] [1,6,1] [2,5,2] [4,3,4] [1,2,4] [1,2,7] [1,2,8] [1,3,2] [1,3,5] [1,4,2] [2,3,4] |
Пример четырехшагового цилиндра Матрица связности
Таблица П.4
Значения коэффициентов 
и 
для расчета числа линий V
по формуле О΄Делла
| D | Р = 0,001 | Р = 0,003 | Р = 0,005 | Р = 0,01 | ||||
| 
|
|
|
|
|
|
| |
| 31,6 10,0 5,62 3,98 3,16 2,68 2,37 2,15 1,99 1,87 1,78 1,71 1,64 1,58 1,54 1,50 1,47 1,44 1,41 1,39 1,37 1,35 1,33 1,31 1,30 1,29 1,28 1,26 1,24 1,22 1,21 1,20 1,19 1,17 1,16 1,15 | 0,7 1,1 1,5 1,9 2,3 2,7 3,1 3,5 3,8 4,2 4,5 4,8 5,1 5,4 5,7 6,0 6,3 6,6 6,9 7,1 7,3 7,5 7,7 7,9 8,1 8,3 8,5 8,9 9,3 9,7 10,1 10,5 10,9 11,4 11,8 12,2 | 18,3 6,93 4,27 3,19 2,63 2,29 2,07 1,90 1,79 1,70 1,62 1,56 1,51 1,47 1,44 1,41 1,38 1,36 1,34 1,32 1,30 1,28 1,27 1,26 1,25 1,24 1,23 1,21 1,20 1,19 1,18 1,17 1,16 1,14 1,13 1,12 | 0,5 0,9 1,3 1,7 2,1 2,5 2,9 3,2 3,5 3,8 4,1 4,4 4,7 4,9 5,1 5,3 5,5 5,7 5,9 6,1 6,3 6,5 6,7 6,9 7,1 7,3 7,5 7,9 8,2 8,5 8,8 9,1 9,4 9,8 10,2 10,8 | 14,2 5,85 3,76 2,88 2,41 2,13 1,93 1,80 1,70 1,62 1,55 1,50 1,46 1,42 1,39 1,36 1,34 1,32 1,30 1,28 1,27 1,26 1,25 1,24 1,23 1,22 1,21 1,19 1,18 1,17 1,16 1,15 1,14 1,13 1,12 1,11 | 0,4 0,8 1,2 1,6 2,0 2,4 2,7 3,0 3,3 3,6 3,9 4,2 4,4 4,6 4,8 5,0 5,2 5,4 5,6 5,8 6,0 6,2 6,4 6,6 6,8 7,0 7,2 7,5 7,7 7,9 8/1 8,3 8,5 9,0 9,5 10,0 | 10,0 4,64 3,16 2,51 2,15 1,93 1,77 1,66 1,58 1,52 1,46 1,42 1,39 1,37 1,33 1,31 1,29 1,27 1,25 1,24 1,23 1,22 1,21 1,20 1,19 1,18 1,17 1,16 1,15 1,14 1,13 1,12 1,12 1,11 1,10 1,09 | 0,3 0,7 1,1 1,5 1,9 2,2 2,5 2,7 2,9 3,1 3,3 3,5 3,7 3,9 4,1 4,3 4,5 4,7 4,9 5,1 5,3 5,5 5,6 5,7 5,8 5,9 6,0 6,2 6,4 6,6 6,8 7,0 7,2 7,5 7,8 8,2 |
|
|
|
