Главная | Обратная связь | Поможем написать вашу работу!

Метод эффективной доступности

Этот метод основан на понятии мгновенной доступности . При обслуживании вызовов в двухзвенной системе мгновенное значение доступности будет изменяться между некоторыми крайними значениями:

Максимальная доступность соответствует случаю, когда все промежуточные линии между звеньями свободны, и при

, (10.7)

где - число выходов из одного коммутатора на звене А;

- число коммутаторов на вене В.

Минимальная доступность соответствует наиболее неблагоприятному по пропускной способности состоянию коммутационной системы: заняты все кроме одного входа в коммутаторе звена А. Минимальная доступность определяется из следующего выражения:

при ; при (10.8)

Можно показать, что потери при двухзвенном включении равны потерям при эквивалентном ему однозвенном включении с тем же числом исходящих линий. Доступность однозвенной схемы с потерями, равными потерям в рассматриваемой двухзвенной схеме, называется эффективной и обозначается .

Доказано, что ,

где - математическое ожидание доступности двухзвенной схемы.

Значение определяется из выражения:

, (10.9)

где - коэффициент пропорциональности, зависящий от типа двухзвенного блока, от нагрузки в направлении, от числа нагрузочных групп и т.д. Значение лежит в пределах от 0,7 до 0,9. Для блоков ГИ обычно принимается .

Величина зависит от связности 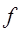и может быть определена:

при ;

при , (10.10)

где - интенсивность нагрузки, обслуженной линиями одного коммутатора звена А, - число входов в один коммутатор на звене А.

После определения эффективной доступности расчет числа линий на выходе двухзвенной схемы сводится к расчету линий на выходе однозвенной неполнодоступной схемы. В частности, можно использовать формулу О’Делла

, (10.11)

где Y – интенсивность нагрузки в направлении, находятся из таблицы 4 Приложения при полученном и заданном значении вероятности потерь P. При дробном значении используют интерполяцию.

Задание 10.

1. Для заданного в таблице 6.2 задания 6 двухзвенного блока ГИ методом Якобеуса рассчитать число линий в НПД пучке для направления от АТСК-3 к проектируемой АТСЭ-4 при величине и качестве обслуживания 5‰. Интенсивность поступающей на один вход блока ГИ нагрузки взять из задания 6.

2. Для этого же блока ГИ методом эффективной доступности рассчитать число линий для направления от АТСК-3 к проектируемой АТСЭ-4 при величине и качестве обслуживания 5‰. Сравнить результаты расчета двумя методами.

Тема 11. Метод построения равномерных неполнодоступных включений: метод цилиндров

Неполнодоступным (НПД) включением называется такое включение линий рассматриваемого пучка, при котором каждому входу коммутационной системы доступна лишь часть линий пучка.

Доступностью НПД пучка линий называется число линий, доступных каждому входу нагрузочной группы. Обозначается .

Необходимость образования НПД включений вызвана конструктивными ограничениями коммутационных приборов и стремлением повысить использование линий в пучке.

Совокупность входов коммутационной схемы, каждому из которых доступны одни и тем же линии пучка, называется нагрузочнойгруппой. Число нагрузочных групп обозначается через .

Необходимым условием НПД включения является неравенство

(11.1)

Отношение называется коэффициентом уплотнения и характеризует среднее число нагрузочных групп, доступных одной линии пучка.

Коэффициент уплотнения находится в пределах . В большинстве случаев оптимальное значение лежит в пределах от 2 до 4.

Число связей между выходами отдельных нагрузочных групп обычно записывается в виде матрицы связности. Диагональный элемент матрицы равен доступности схемы. Каждый элемент матрицы 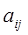показывает число связей между нагрузочными группами и .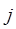

В соответствии с порядком искания свободных линий в НПД схемах различают: упорядоченное искание (АТСДШ); случайное искание (АТСК).

Равномерным включением называется такое НПД включение, при котором число нагрузочных групп, обслуживаемых каждой линией, одинаково или отличается на единицу. Равномерное включение используется в системах со случайным исканием.

В зависимости от способа запараллеливания выходов различных нагрузочных групп неполнодоступные включения делятся на прямые, с перехватом, со сдвигом.

Перехват со сдвигом часто выполняется в виде циклических схем, называемых цилиндрами. Цилиндр – элементарная равномерная схема с одинаковым сдвинутым включением. Цилиндр характеризуется размером (количеством охватываемых выходов каждой нагрузочной группы) и величиной наклона. Цилиндр размера называется - шаговым. Наклон - шагового цилиндра характеризуется числом параметров .

Выбор оптимальной структуры равномерной НПД схемы производится по следующим правилам:

1) каждая линия должна быть доступна одинаковому числу нагрузочных групп (или отличаться на единицу);

2) каждая нагрузочная группа должна иметь одинаковое число обслуживающих линий со всякой другой нагрузочной группой;

3) каждая линия объединяет соседние выходы.

Для выполнения правила 1 производится расчет равномерной НПД схемы. Для этого:

а) определяется коэффициент уплотнения .

Величина может быть дробным числом. Тогда часть линий из общего пучка линий V объединяют по выходов нагрузочных групп, где - целая часть числа. Другая часть линий объединяет по выходов нагрузочных групп;

б) находится число линий и решением системы уравнений

(11.2)

Откуда

(11.3)

В инженерной практике используется следующий простой прием: результат деления представляется в виде правильной дроби без сокращения. Если значение получилось целое без остатка, то каждая линия запараллеливает выходы нагрузочных групп. Если в результате получилась дробь следующего вида (без сокращений) , то линий запараллеливают по нагрузочных групп, а - по нагрузочных групп.

Для выполнения правил 2) и 3) необходимо при построении равномерной НПД схемы использовать цилиндры с различной величиной наклона (с различными параметрами).

Размерность используемых цилиндров определяется величинами и .

Число цилиндров зависит от числа нагрузочных групп и величин и . Число цилиндров размерностью составит 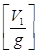, а число цилиндров размерностью .

Типы цилиндров, легко приводящих схему к равномерной, и их первые строки матриц связности приведены в таблицах П.2,3 Приложения.

В практических случаях не удается построить равномерную НПД схему, используя только цилиндры. Оставшиеся выходы объединяются с наименьшим нарушением указанных трех правил.

Для оценки полученной равномерной НПД схемы строится матрица связности. Включение будет равномерным, если элементы внутри матицы не будут отличаться более чем на единицу, а сумма по строке должна быть одинаковой или отличатся не более чем на единицу.

Пример равномерного НПД включения показан на рис.11.1.

Задание 11.

Построить схему равномерного НПД включения линий для направления от АТСК-3 к проектируемой АТСЭ-4 на выходе двухзвенного блока ГИ. Для оценки выполненного включения составить матрицу связности. Число линий V взять из результатов расчета задания 9, число нагрузочных групп выбрать таким образом, чтобы выполнялось условие =2÷4.

б)

g
	*
		*
			*
				*
					*
						*

следовательно, 6 линий

включаются в выходы

2+1=3 нагрузочных групп,

а 21-6=15 линий в выходы

2-х нагрузочных групп.

Рис.11.1. Пример равномерного НПД включения: g=6; D=8; V=21.

а) схема равномерного НПД включения;

б) матрица связности.

Тема 12. Метод вероятностных графов для расчета пропускной способности многозвенных коммутационных схем

Коммутационные поля координатных и квазиэлектронных АТС строятся на основе многозвенных схем. Расчет многозвенных схем более сложен, чем расчет однозвенных НПД схем. Поэтому для оценки пропускной способности многозвенных схем используются приближенные инженерные методы и моделирование коммутационных схем.

Одним из приближенных методов расчета многозвенных коммутационных схем является метод вероятностных графов.

Сущность метода заключается в том, что для определения пропускной способности многозвенной схемы рассматривается не вся схема, а только та ее часть, которая содержит все возможные соединительные пути от заданного входа к выбранному выходу. При этом рассматривается не сама схема, а ее модель, в которой коммутаторы заменяются точками и называются вершинами, а соединительные пути между коммутаторами – дугами графа.

Предполагается, что дуги графа, соединяющие соседние вершины, занимаются независимо от состояния дуг между другими вершинами с одинаковой вероятностью , равной среднему использованию дуги, т.е. частному от деления нагрузки , обслуженной промежуточными линиями между соседними звеньями и , на число этих линий : .

При определении вероятности потерь любого сложного графа используют выражение для вычисления следующих простых графов.

Рис. 12.1. Простейшие вероятностные графы

Если граф состоит только из одной дуги с вероятностью занятости (рис.12.1а), то вероятность потерь в коммутационной схеме, отображаемой этим графом, .

Вероятность потерь в графе, состоящем из параллельно включенных дуг (рис.12.1б)

. (12.1)

Вероятность потерь в графе, состоящем из последовательно включенных дуг с вероятностями занятости (рис.12.1в):

(12.2)

Вероятность потерь в параллельно – последовательном графе (рис.12.1г):

(12.3)

Задание 12.

1.Рассчитать структурные параметры и построить схему группообразования блока абонентского искания (АИ) АТСК-3 в координатном виде. Структура коммутационной схемы и типы МКС, на которых реализовано каждое звено, заданы в таблице 12.1 в соответствии с номером варианта.

Таблица 12.1

№ вар.	Тип МКС, на котором реализовано	Параметры блока АИ
Звено А	Звено В	Звено С	Звено D
	20х10х6	20х10х6	20х10х6	10х20х6
	10х10х12	10х10х12	10х10х12	10х20х6
	10х10х12	10х10х12	10х10х12	10х10х12
	20х10х6	20х10х6	20х10х6	10х20х6
	10х10х12	10х10х12	10х10х12	20х10х6
	10х10х12	10х10х12	20х10х6	10х20х6
	20х10х6	10х10х12	10х10х12	10х10х12
	10х10х12	20х10х6	10х10х12	10х20х6
	10х10х12	10х10х12	20х10х6	10х20х6
	20х10х6	20х10х6	10х10х12	10х10х12
	10х10х12	10х10х12	10х10х12	10х20х6
	10х10х12	10х10х12	20х10х6	10х20х6
	20х10х6	20х10х6	10х10х12	10х20х6
	10х10х12	10х10х12	10х10х12	10х10х12
	10х10х12	20х10х6	20х10х6	10х20х6
	20х10х6	20х10х6	20х10х6	10х20х6
	10х10х12	10х10х12	10х10х12	10х20х6
	10х10х12	10х10х12	10х10х12	10х10х12
	20х10х6	20х10х6	20х10х6	10х20х6
	10х10х12	10х10х12	10х10х12	20х10х6
	10х10х12	10х10х12	20х10х6	10х20х6
	20х10х6	10х10х12	10х10х12	10х10х12
	10х10х12	20х10х6	10х10х12	10х20х6
	10х10х12	10х10х12	20х10х6	10х20х6
	20х10х6	20х10х6	10х10х12	10х10х12
	10х10х12	10х10х12	10х10х12	10х20х6
	10х10х12	10х10х12	20х10х6	10х20х6
	20х10х6	20х10х6	10х10х12	10х20х6
	10х10х12	10х10х12	10х10х12	10х10х12
	10х10х12	20х10х6	20х10х6	10х20х6

2.Построить вероятностные графы и рассчитать вероятность потерь методом вероятностных графов по исходящей и входящей связи для блока абонентского искания Удельную исходящую абонентскую нагрузку принять равной входящей а_исх=а_вх=а из задания 3. Для четырехзвенной схемы число блоков АВ принять равным 10, число блоков CD – 4.

Пример решения задачи.

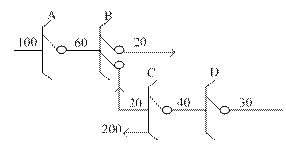
Пусть задана четырехзвенная ступень абонентского искания (рис.12.2).