 |
Инерциальные системы отсчета
|
|
|
|
III. Основное уравнение динамики
(динамика материальной точки)
Законы Ньютона справедливы только в инерциальных системах отсчета (ИСО). Инерциальной является такая система отсчета, в которой любое тело, не взаимодействующее с другими телами, движется равномерно и прямолинейно. В ИСО сила есть результат взаимодействия тел между собой, и важно учесть и проанализировать эти силы.
Если силы действуют не по одной прямой, то выбирают две взаимно перпендикулярные оси (два направления X и Y), лежащие в плоскости действия сил. В случае прямолинейного движения одну из осей (X) направляют вдоль ускорения 
, а другую (Y) – перпендикулярно вектору . В общем случае криволинейного движения одну ось направляют вдоль тангенциального ускорения 
(то есть по касательной к кривой), другую - вдоль нормального ускорения 
.
При движении тела по поверхности какого-либо другого тела между ними возникает взаимодействие. При этом сила, направленная перпендикулярно поверхностям соприкасающихся тел, называется нормальной реакцией опоры или силой нормального давления. А сила, направленная по касательной к поверхностям соприкасающихся тел, называется силой трения. Сила трения подразделяется на – силу трения покоя и силу трения скольжения. Сила трения покоя существует между двумя соприкасающимися телами, когда их относительная скорость равна нулю. Сила трения покоя может изменяться от нуля до максимального значения 
, где 
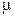- коэффициент трения, N - сила реакции опоры. В промежутке от нуля до максимального значения 
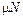сила трения покоя равна по величине равнодействующей всех сил, действующих на тело, но противоположно ей направлена. Сила трения скольжения, как и максимальная сила трения покоя, пропорциональна силе нормального давления 
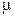, где - коэффициент трения скольжения, а относительная скорость двух тел не равна нулю. Зачастую бывает трудно определить направление силы трения, поэтому следует помнить простое правило: сила трения всегда направлена в сторону, противоположную возможному проскальзыванию.
|
|
|
Законы Ньютона можно использовать и в неинерциальных системах, если наряду с силами, обусловленными взаимодействиями тел между собой, ввести силы инерции. Силы инерции зависят от характера движения и от свойств неинерциальной системы отсчета. Для нахождения сил инерции необходимо знать, как движется неинерциальная система отсчетаотносительно инерциальной системы, т.е. знать характер движения и его кинематические параметры.
Инерциальные системы отсчета
В формулировкевторого закона Ньютона ничего не говорится о точке приложения силы, о форме и размере тел. Поэтому этот закон можно применять как для материальных точек, так и для поступательно движущихся твердых тел. Поступательное движение возникает тогда, когда линии действия всех сил или результирующей силы проходят через центр масс тела.
Для решения задач динамики составляется уравнение движения, выражающее второй закон Ньютона. При этом рекомендуется:
1) сделать чертеж и изобразить все силы, действующие на данное тело. Выражение «на тело действует сила» означает, что данное тело взаимодействует с другим телом, в результате чего приобретает ускорение. Следовательно, к данному телу всегда приложено столько сил, сколько имеется других тел, с которыми оно взаимодействует,
2) выбрать координатные оси и записать уравнения движения в проекциях на них,
3) если требуется определить действие одной части системы на другую, необходимо разделить систему на части, зарисовать одну из частей, расставить силы, действующие на нее и записать уравнения движения,
|
|
|
4) если число записанных уравнений меньше числа неизвестных, то необходимо определить кинематические и динамические связи между неизвестными. Таким образом, получают систему уравнений, число которых равно числу неизвестных.
Как было отмечено ранее, законы Ньютона справедливытолько в инерциальных системах отсчета. Во многих задачах систему отсчета, связанную с Землей, можно считать инерциальной, если пренебречь ее вращением относительно собственной оси.
Решение задач
3.1. Тело массы m движется по горизонтальной плоскости под действием силы 
, направленной под углом 
к горизонту. Начальная скорость равна нулю. Найти:
а) ускорение тела, если коэффициент трения между телом и плоскостью равен ,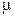
б) величину силы, при которой движение будет равномерным,
в) угол , при котором сила будет минимальна при равномерном движении, а так же величину этой силы.
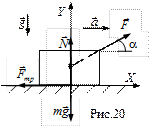Решение. а) Покажем силы, действующие на тело. На тело действуют четыре силы: сила тяжести 
, сила нормальной реакции опоры 
, сила трения 
и сила 
.
Направим ось X в горизонтальном направлении по направлению движения тела, а ось Y - вертикально вверх (рис.20). Запишем основной закон динамики в проекциях на эти оси:
,
.
,
так как вдоль оси Y тело не движется. Учитывая, что модуль силы трения скольжения равен 
, решим полученную систему уравнений и найдем ускорение тела:
.
б) Движение будет равномерным при 
, то есть
.
Отсюда
.
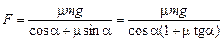в) Чтобы найти угол , при котором сила будет минимальна, необходимо продифференцировать полученное выражение для силы по углу и, приравняв полученное выражение к нулю, выразить из него искомый угол:
,
.
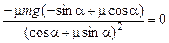Учитывая, что 
, получим
.
Подставив полученное значение угла в выражение для величины силы с учетом соотношения 
, найдем ее минимальное значение:
.
|
|
|
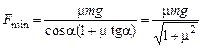