 |
Теперь усложним задачу и рассмотрим случай, когда сила трения, действующая на тело, – переменная, то есть зависит от пройденного пути.
|
|
|
|
3.6*. Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол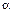 
с горизонтом. Коэффициент трения зависит от пройденного пути 
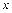по закону 
, где 
- постоянная. Найти путь, пройденный бруском до остановки.
Решение. Рассмотрим силы, действующие на брусок при его движении вниз. На брусок действуют три силы: сила тяжести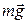 
, сила нормальной реакции опоры 
и сила трения 
(рис.23).
Направим ось X вдоль наклонной плоскости вниз, а ось Y - перпендикулярно плоскости вверх. Запишем основной закон динамики в проекциях на оси X и Y соответственно:
,
.
Учитывая, что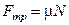 
, запишем уравнение движения тела:
,
.
По определению 
, 
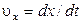откуда 
, поэтому, произведя замену переменных, получим:
.
Разделим переменные
,
и проинтегрировав левую часть этого выражения от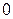 
до 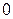(скорость бруска в момент остановки равна нулю 
), а правую от 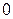до 
, найдем путь, пройденный бруском до остановки:
,
,
,
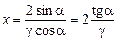где координата x равна пройденному пути.
3.7. На горизонтальной плоскости расположены два связанных друг с другом нитями тела массами m1 и m2. На нити, прикрепленной к телу массой m2 и перекинутой через неподвижный блок, подвешено тело массой m0. Массы блока и нитей пренебрежимо малы, трения в блоке нет. Найти ускорение, с которым опускается тело массой m0, и силу натяжения нити, связывающей тела m1 и m2, если коэффициент трения между горизонтальной плоскостью и телами m1 и m2 равен 
.
Решение. Покажем силы, действующие на тела при движении тела массой m0 вниз (рис.24). Направим ось Y в направлении движения тела массой m0, а ось X – перпендикулярно ей по горизонтали влево. Поскольку тела связаны невесомыми и нерастяжимыми нитями, то модули сил натяжения для каждой нити равны между собой и все тела движутся с одинаковым по модулю ускорением:
|
|
|
и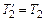 
,
,
.
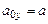Учитывая это, запишем уравнения движения для каждого бруска в проекциях на оси X и Y:
, 
, 
.
, 
, 
.
.
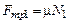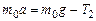Решим полученную систему уравнений и найдем ускорение, с которым опускается тело массой m0:
.
Тогда, сила натяжения нити, связывающей тела m1 и m2 равна
Теперь рассмотрим динамику материальной точки, движущейся по окружности. В этом случае одну ось направляют вдоль тангенциального ускорения, то есть по касательной к траектории, другую - вдоль нормального ускорения.
3.8. Шарик, подвешенный на нити, качается в вертикальной плоскости. Найти ускорение шарика в крайней точке, если угол отклонения нити от вертикали равен 
.
Решение. Шарик движется неравномерно по окружности, радиус которой равен длине нити l. На шарик действуют сила натяжения нити 
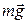и сила тяжести (рис.25).
Согласно второму закону Ньютона
.
При неравномерном движении по окружности полное ускорение равно
,
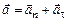где 
- центростремительное (нормальное) ускорение, направленное по радиусу окружности к ее центру, 
- касательное (тангенциальное) ускорение, совпадающее по направлению с направлением скорости.
Направим орт 
из точки 1 вдоль нити к центру окружности, а орт 
- перпендикулярно орту . В верхней точке 1 скорость шарика равна нулю, следовательно, его центростремительное ускорение также равно нулю 
. Это означает, что полное ускорение шарика в точке 1 будет определяться только его тангенциальным ускорением 
. Найдем полное ускорение шарика, воспользовавшись уравнением движения в проекциях на орт :
.
Ускорение шарика в крайней точке равно
.
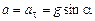3.9. Самолет делает «мертвую петлю» радиусом R. В верхней точке его скорость равна 
. В кабине находится человек, масса которого равна m. Найти силу, прижимающую человека к сидению в верхней точке траектории.
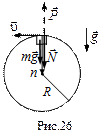Решение. По условию скорость самолета в верней точки траектории равна 
. В этой точке сила, действующая на человека складывается из направленных вниз силы тяжести и силы реакции опоры, действующей на человека со стороны сиденья (рис. 26). Направим ось n к центру траектории и запишем уравнение движения в проекциях на эту ось
|
|
|
,
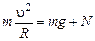где 
- ускорение летчика в верхней точке траектории.
Сила, прижимающая человека к сиденью (по определению это вес человека), определим по третьему закону Ньютона. Она равна по величине силе 
, но противоположно ей направлена (рис.26)
.
Поэтому величина этой силы равна
.
Если 
, то человек испытывает «невесомость».
3.10. Для подготовки летчиков-космонавтов к перегрузкам применяют специальные центрифуги. При какой частоте вращения центрифуги радиуса R спинка сиденья давит на летчика с такой же силой, которая возникает при подъеме ракеты с ускорением 
.
Решение. На тело в ракете, движущейся вертикально вверх с ускорением , действуют сила тяжести 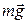, направленная вертикально вниз, и сила 
, направленная вертикально вверх со стороны сиденья (рис.27). Запишем уравнение движения в проекциях на ось Y, положительное направление которой совпадает с направлением ускорения 
,
откуда
.
При движении центрифуги сила, с которой спинка сиденья давит на летчика, сообщает ему центростремительное ускорение 
, где 
- угловая скорость вращения центрифуги. Запишем уравнение движения в проекциях на ось X (рис.28):
.
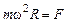Выразим угловую скорость через частоту вращения
и, решив совместно последние три уравнения, получим частоту вращения центрифуги
.
|
|
|
