 |
Неинерциальные системы отсчета
|
|
|
|
Законы Ньютона, справедливые в инерциальных системах отсчета, можно использовать и в неинерциальных системах, если наряду с силами, обусловленными взаимодействиями тел между собой, ввести силы инерции. Чаще всего рассматриваются два основных типа неинерциальных систем:
а) системы, движущиеся относительно какой-либо инерциальной системы (например, относительно Земли) поступательно, прямолинейно и ускоренно. В таких системах на тела действует сила инерции 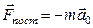 , где
, где  - ускорение неинерциальной системы отсчета,
- ускорение неинерциальной системы отсчета,
б) системы, вращающиеся с постоянной угловой скоростью относительно какой-либо инерциальной системы. В таких системах на все тела и покоящиеся, и движущиеся действует центробежная сила инерции  , где
, где  - радиус-вектор, перпендикулярный оси вращения и характеризующий положение частицы относительно этой оси. На движущиеся в такой системе отсчета тела помимо центробежной силы инерции действует еще и сила Кориолиса, или кориолисова сила инерции, равная
- радиус-вектор, перпендикулярный оси вращения и характеризующий положение частицы относительно этой оси. На движущиеся в такой системе отсчета тела помимо центробежной силы инерции действует еще и сила Кориолиса, или кориолисова сила инерции, равная  , где
, где  - скорость тела в неинерциальной системе отсчета.
- скорость тела в неинерциальной системе отсчета.
Особенности сил инерции заключаются в том, что
1) они обусловлены не взаимодействием тел между собой, а свойствами самих неинерциальных систем отсчета, и поэтому они не подчиняются третьему закону Ньютона,
2) они существуют только в неинерциальных системах отсчета и зависят от их типа,
3) они всегда пропорциональны массе тела.
Решение задач
3.11. В вагоне, движущемся с ускорением  по горизонтальной плоскости, к штативу на нити подвешен шарик. Найти угол отклонения нити от вертикали.
по горизонтальной плоскости, к штативу на нити подвешен шарик. Найти угол отклонения нити от вертикали.
Решение. Система отсчета, связанная с вагоном, является неинерциальной системой отсчета, поскольку она движется поступательно с ускорением относительно инерциальной системы отсчета, связанной с Землей. В этой неинерциальной системе отсчета шарик неподвижен, следовательно, сумма сил, действующих на него равна нулю. На шарик действуют сила натяжения нити  , сила тяжести
, сила тяжести 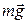 и сила инерции
и сила инерции  , направленная в сторону, противоположную ускорению вагона
, направленная в сторону, противоположную ускорению вагона  :
:
|
|
|
 .
.
 Выберем оси X и Y, как показано на рис.29 и запишем это уравнение в проекциях на них:
Выберем оси X и Y, как показано на рис.29 и запишем это уравнение в проекциях на них:
 ,
,
 .
.
Решив совместно полученную систему уравнений, найдем угол отклонения нити от вертикали:
 .
.
То есть угол отклонения нити не зависит от массы шарика и длины нити, и он тем больше, чем больше ускорение вагона.
 3.12*. С каким минимальным ускорением следует перемещать в горизонтальном направлении брусок А (рис.30), чтобы тела 1 и 2 не двигались относительно него. Массы тел одинаковы, коэффициент трения между бруском и обоими телами равен
3.12*. С каким минимальным ускорением следует перемещать в горизонтальном направлении брусок А (рис.30), чтобы тела 1 и 2 не двигались относительно него. Массы тел одинаковы, коэффициент трения между бруском и обоими телами равен  . Массы блока и нити пренебрежимо малы, трения в блоке нет.
. Массы блока и нити пренебрежимо малы, трения в блоке нет.
Решение. Направим ось X в направлении движения бруска А влево, а ось Y -перпендикулярно вниз. Покажем силы, действующие на тела 1 и 2 (рис.30). Тела 1 и 2 по условию должны покоится относительно движущегося бруска А, поэтому, если связать систему отсчета с этим бруском, то ускорения тел 1 и 2 в этой неинерциальной системе (НСО) должны быть равны нулю. В поступательно движущейся неинерциальной системе отсчета на тела 1 и 2 будут действовать силы инерции  и
и  , где
, где  - ускорение, с которым движется брусок А (рис.30).
- ускорение, с которым движется брусок А (рис.30).
Поскольку тела связаны невесомой нитью, то модули сил натяжения равны между собой  .
.
Запишем для каждого груза уравнение движения в НСО в проекциях на оси X и Y соответственно:
тело 1:  ,
,  .
.
тело 2:  ,
,  .
.
Учитывая, что  - по условию, и исключив T из первого и последнего уравнений, получим выражение для ускорения бруска A
- по условию, и исключив T из первого и последнего уравнений, получим выражение для ускорения бруска A
 .
.
Из полученного выражения видно, что минимальное значение ускорения бруска соответствует максимальным значениям сил трения  и
и  , которые являются силами трения покоя и их максимальные значения соответственно равны
, которые являются силами трения покоя и их максимальные значения соответственно равны  и
и  , откуда, подстановкой
, откуда, подстановкой  и
и  , получим
, получим
|
|
|
 ,
,
после преобразования минимальное ускорение бруска А равно
 .
.
3.13. Определить, в каком направлении и с какой скоростью относительно Земли должен двигаться поезд на северной широте  , чтобы результирующая сил инерции, действующих в системе отсчета, связанной с Землей, была равна нулю.
, чтобы результирующая сил инерции, действующих в системе отсчета, связанной с Землей, была равна нулю.

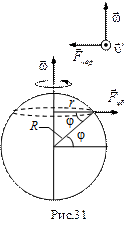 Решение. Система отсчета, связанная с Землей является неинерциальной системой отсчета, поскольку Земля вращается вокруг своей оси. В неинерциальной вращающейся системе отсчета на движущиеся тела действуют центробежная сила инерции
Решение. Система отсчета, связанная с Землей является неинерциальной системой отсчета, поскольку Земля вращается вокруг своей оси. В неинерциальной вращающейся системе отсчета на движущиеся тела действуют центробежная сила инерции  (связанная с вращением системы отсчета) и сила инерции Кориолиса
(связанная с вращением системы отсчета) и сила инерции Кориолиса  (связанная с движением тела в неинерциальной системе отсчета). Первая направлена от оси вращения перпендикулярно к ней и равна по величине
(связанная с движением тела в неинерциальной системе отсчета). Первая направлена от оси вращения перпендикулярно к ней и равна по величине  , где
, где  - угловая скорость вращения Земли, r - расстояние до оси вращения. Это расстояние (рис.31) равно
- угловая скорость вращения Земли, r - расстояние до оси вращения. Это расстояние (рис.31) равно  , где R - радиус Земли. Вторая сила - сила Кориолиса - определяется выражением
, где R - радиус Земли. Вторая сила - сила Кориолиса - определяется выражением  , и ее направление зависит от направления скорости тела относительно Земли
, и ее направление зависит от направления скорости тела относительно Земли  . Для того, чтобы результирующая сил инерции
. Для того, чтобы результирующая сил инерции  была равна нулю, кориолисова сила инерции должна быть направлена противоположно центробежной силе инерции и равна ей по величине. Нетрудно убедиться, что в этом случае поезд должен двигаться с востока на запад (ориентация векторов
была равна нулю, кориолисова сила инерции должна быть направлена противоположно центробежной силе инерции и равна ей по величине. Нетрудно убедиться, что в этом случае поезд должен двигаться с востока на запад (ориентация векторов  ,
,  и
и  на рис.31, значок показывает, что вектор скорости
на рис.31, значок показывает, что вектор скорости  направлен на нас). Величина скорости
направлен на нас). Величина скорости  определяется из условия равенства сил инерции по формуле:
определяется из условия равенства сил инерции по формуле:
 .
.
Определим скорость движения поезда
 .
.
Здесь угловая скорость вращения Земли  , где
, где  часа - длительность суток.
часа - длительность суток.
3.14. Гладкий горизонтальный диск вращают относительно Земли, вращение которой не учитывается, с угловой скоростью  вокруг вертикальной оси, проходящей через его центр. В центре диска поместили небольшую шайбу массой m и сообщили ей толчком горизонтальную скорость
вокруг вертикальной оси, проходящей через его центр. В центре диска поместили небольшую шайбу массой m и сообщили ей толчком горизонтальную скорость  . Найдите величину силы Кориолиса, действующей на шайбу в системе отсчета связанной с диском, через время t после начала ее движения.
. Найдите величину силы Кориолиса, действующей на шайбу в системе отсчета связанной с диском, через время t после начала ее движения.
 Решение. Система отсчета, связанная с вращающимся диском является неинерциальной системой отсчета. В этой системе на движущуюся шайбу действует искомая сила Кориолиса, определяемая выражением:
Решение. Система отсчета, связанная с вращающимся диском является неинерциальной системой отсчета. В этой системе на движущуюся шайбу действует искомая сила Кориолиса, определяемая выражением:
|
|
|
 ,
,
ее направление зависит от направления скорости тела относительно диска  . Из условия задачи известна скорость шайбы
. Из условия задачи известна скорость шайбы  относительно Земли, которая, в условиях данной задачи, является инерциальной системой отсчета. Запишем связь между скоростями шайбы в этих системах отсчета:
относительно Земли, которая, в условиях данной задачи, является инерциальной системой отсчета. Запишем связь между скоростями шайбы в этих системах отсчета:
 .
.
 Выразим из последнего выражения вектор
Выразим из последнего выражения вектор  и представим его направление на рис.32 (на рисунке представлен вид сверху, значок показывает направление угловой скорости
и представим его направление на рис.32 (на рисунке представлен вид сверху, значок показывает направление угловой скорости  диска). И, как видно из рисунка, угол между векторами
диска). И, как видно из рисунка, угол между векторами  и
и  равен
равен  , а модуль вектора
, а модуль вектора  равен
равен
 .
.
Поскольку  и угол между векторами
и угол между векторами  и
и  равен
равен  , найдем силу Кориолиса, действующей на шайбу в системе отсчета связанной с диском, через время t после начала ее движения:
, найдем силу Кориолиса, действующей на шайбу в системе отсчета связанной с диском, через время t после начала ее движения:
 .
.
3.15. Гладкий стержень АВ вращают в горизонтальной плоскости с угловой скоростью  вокруг вертикальной оси, проходящей через его конец А. По стержню скользит муфта массы m, стартовавшая в точке А со скоростью (относительно стержня)
вокруг вертикальной оси, проходящей через его конец А. По стержню скользит муфта массы m, стартовавшая в точке А со скоростью (относительно стержня) 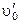 . Найдите величину силы Кориолиса, действующую на муфту в момент, когда она оказалась на расстоянии
. Найдите величину силы Кориолиса, действующую на муфту в момент, когда она оказалась на расстоянии 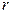 от оси вращения.
от оси вращения.
 Решение. Система отсчета, связанная с вращающимся в горизонтальной плоскости стержнем является неинерциальной системой отсчета. В неинерциальной вращающейся системе отсчета на движущиеся тела действуют центробежная сила инерции
Решение. Система отсчета, связанная с вращающимся в горизонтальной плоскости стержнем является неинерциальной системой отсчета. В неинерциальной вращающейся системе отсчета на движущиеся тела действуют центробежная сила инерции  (связанная с вращением системы отсчета) и сила инерции Кориолиса
(связанная с вращением системы отсчета) и сила инерции Кориолиса  (связанная с движением тела в неинерциальной системе отсчета). Так как движение муфты происходит в горизонтальной плоскости, то силы, действующие на муфту в вертикальном направлении, компенсируют друг друга и поэтому на рисунке не показаны. Сила Кориолиса - определяется выражением:
(связанная с движением тела в неинерциальной системе отсчета). Так как движение муфты происходит в горизонтальной плоскости, то силы, действующие на муфту в вертикальном направлении, компенсируют друг друга и поэтому на рисунке не показаны. Сила Кориолиса - определяется выражением:  , и имеет направление перпендикулярное направлению движения муфты по стержню (рис.33). Поэтому муфта вдоль стержня движется под действием одной силы - центробежной, направленной от оси вращения перпендикулярно к ней и равной по величине
, и имеет направление перпендикулярное направлению движения муфты по стержню (рис.33). Поэтому муфта вдоль стержня движется под действием одной силы - центробежной, направленной от оси вращения перпендикулярно к ней и равной по величине  , где
, где  -угловая скорость вращения стержня,
-угловая скорость вращения стержня, 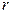 - расстояние от муфты до оси вращения. Запишем уравнение движения муфты:
- расстояние от муфты до оси вращения. Запишем уравнение движения муфты:
|
|
|
 .
.
Для удобства решения умножим и разделим левую часть уравнения движения на  :
:
 .
.
Учитывая, что по определению  , разделим переменные в последнем уравнении:
, разделим переменные в последнем уравнении:
 .
.
Проинтегрировав левую часть этого выражения от 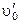 до
до  , а правую от 0 до
, а правую от 0 до 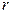
 ,
,
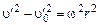 ,
,
найдем скорость муфты в момент, когда она находится на расстоянии 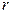 от оси вращения:
от оси вращения:
 .
.
Поскольку ( ), сила Кориолиса, действующая на муфту в этой точке, будет равна:
), сила Кориолиса, действующая на муфту в этой точке, будет равна:
 .
.
|
|
|


