 |
Теперь усложним задачу и решим ее для случая, когда сила, действующая на тело - переменная.
|
|
|
|
3.2*. На тело массы m, лежащее на гладкой горизонтальной плоскости в момент t= 0 начала действовать сила, зависящая от времени как 
, где k - постоянная. Направление этой силы все время составляет угол 
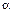с горизонтом. Найти:
а) скорость тела в момент отрыва от плоскости;
б) путь, пройденный телом к этому моменту.
Решение. а)Расставим силы, действующие на тело. На тело действуют три силы: сила тяжести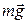 
, сила нормальной реакции опоры 
и переменная сила 
.
Направим ось X в горизонтальном направлении по направлению движения тела, а ось Y - вертикально вверх (рис.21).
Запишем уравнение движения тела в проекциях на оси X и Y, учитывая что 
:
, (1)
. (2)
Введем 
– момент отрыва, тогда уравнения (1) и (2) будут справедливы при 
. В момент отрыва N=0, поэтому, подставив в уравнение (2), найдем время отрыва тела от поверхности:
.
Разделив переменные, приведем уравнение (1) к виду удобному для интегрирования
.
Проинтегрировав левую часть этого выражения от 0до 
, а правую от 0 до t, найдем зависимость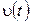 
.
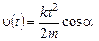Подставив в последнее выражение время отрыва тела 
, найдем скорость тела в момент отрыва
.
б) Путь S, пройденный телом за время t, равен
.
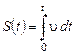Проведя интегрирование, получим
.
Подставив в последнее выражение время отрыва тела , найдем путь тела, пройденный до отрыва
.
3.3. Частица движется вдоль оси x по закону 
, где 
и 
- положительные постоянные. В момент t= 0сила, действующая на частицу, равна 
. Найти значения 
силы в точках поворота и в момент, когда частица опять окажется в точке x= 0.
Решение. Основное уравнение динамики движения материальной точки (второй закон Ньютона) в проекциях на ось X имеет вид:
.
Найдем 
, воспользовавшись определением:
,
тогда:
.
Найдем массу m из начальных условий:
|
|
|
,
.
Найдем моменты времени, когда частица находится в точках поворота. В точках поворота первая производная 
по времени равна 0 
:
,
.
Данное уравнение имеет два корня 
, который соответствует моменту поворота, и 
, который соответствует начальному состоянию движения. Подставляя найденные значения m и t в исходное уравнение, получим значение силы в точке поворота:
.
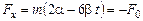Определим моменты времени, когда частица опять окажется в точке x= 0:
,
.
Данное уравнение имеет два корня 
и 
, который соответствует начальному состоянию движения.
Подставляя найденные значения m и t в исходное уравнение, получим значение силы в момент, когда частица опять окажется в точке x= 0:
.
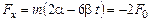3.4. В момент t=0 частица массы m начинает двигаться под действием силы 
, где 
и 
- постоянные. Найти:
а) сколько времени частица будет двигаться до первой остановки,
б) какой путь она пройдет за это время.
Решение. Скорость частицы и пройденный ею путь определяются следующими формулами:
и 
.
Ускорение найдем из уравнения движения частицы (второй закон Ньютона):
.
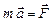тогда из условия задачи
.
Направим ось X вдоль , тогда последнее уравнение в проекциях на эту ось примет вид
.
По определению
.
В момент остановки 
, поэтому:
, при 
.
Найдем, сколько времени частица будет двигаться до первой остановки (
):
.
Тогда путь, который частица пройдет за это время будет равен:
.
Проведя интегрирование, получим:
.
3.5. Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол 
с горизонтом. Найти коэффициент трения, если время подъема оказалось в 
раза меньше времени спуска.
Решение. Проанализируем силы, действующие на тело. На брусок действуют три силы: сила тяжести 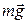, сила нормальной реакции опоры и сила трения 
(рис.22).
Направим ось X вдоль наклонной плоскости вниз, а ось Y – перпендикулярно плоскости вверх.
|
|
|
Рассмотрим движение бруска вверх. Запишем основной закон динамики в проекциях на оси X и Y соответственно:
,
.
Учитывая, что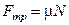 
, найдем ускорение тела во время подъема:
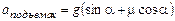. (1)
Рассмотрим движение бруска вниз. Составим уравнение движения в проекциях на оси X и Y соответственно, принимая во внимание, что сила трения будет направлена в противоположную сторону
,
.
Тогда ускорение тела во время спуска будет равно:
. (2)
Найдем связь между временем и ускорением спуска и подъема. Движение тела описывается кинематическими уравнениями
,
.
С учетом того, что в момент остановки тела при его подъеме вверх 
, 
и 
, последние два уравнения примут вид
,
.
Откуда 
. Так как и при подъеме и при спуске тело прошло одно и тоже расстояние, то соответствующие значения времени и ускорения связаны соотношениями
. (3)
Решая систему из уравнений (1), (2) и (3), получим выражение для коэффициента трения
.
|
|
|
