 |
IV. Законы изменения и сохранения импульса системы
|
|
|
|
Импульс материальной точки есть векторная величина
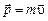 .
.
Импульс системы материальных точек равен векторной сумме импульсов всех частиц, образующих систему:
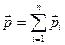 .
.
Ценность закона сохранения импульса для решения задач динамики в том, что он связывает начальное и конечное состояние импульса замкнутой системы, позволяет исключить из рассмотрения внутренние силы, то есть силы взаимодействия частей системы. Поэтому закон применяют в тех задачах, в которых силы взаимодействия между отдельными телами системы являются величинами переменными, причем характер их изменения во времени сложен или вообще неизвестен (например, силы, возникающие при ударе).
Закон сохранения импульса утверждает, что в замкнутой системе импульс есть величина постоянная. Таким образом, этот закон можно применять только к замкнутой системе, то есть к такой системе, на которую извне не действуют другие тела. Очевидно, что понятие замкнутой системы имеет смысл только по отношению к инерциальным системам отсчета, поскольку в неинерциальных системах отсчета всегда действуют силы инерции, играющие роль внешних сил.
Импульс может сохраняться и у незамкнутой системы, при условии что
1) сумма внешних сил равна нулю;
2) если проекция результирующей внешней силы, на некоторое направление равна нулю, то сохраняется не сам импульс, а его проекция на это направление 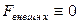 ,
, 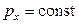 . (Например, летящий снаряд разрывается в какой-либо точке траектории. Система является незамкнутой, так как присутствует сила тяжести
. (Например, летящий снаряд разрывается в какой-либо точке траектории. Система является незамкнутой, так как присутствует сила тяжести 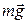 . Однако, проекция этой силы на горизонтальную ось равна нулю, поэтому можно записать
. Однако, проекция этой силы на горизонтальную ось равна нулю, поэтому можно записать 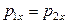 );
);
3) если взаимодействие тел происходит очень быстро, например, удар, взрыв, выстрел, то изменением импульса системы можно пренебречь. Согласно закону изменения импульса системы 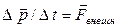 .
. 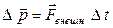 , если
, если 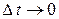 (например, взрыв), то можно считать, что
(например, взрыв), то можно считать, что 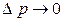 и импульс системы сохраняется.
и импульс системы сохраняется.
|
|
|
При составлении уравнений на основании закона сохранения импульса необходимо:
1) Сделать схематический чертеж, выбрать систему отсчета. Скорости всех рассматриваемых тел отсчитывать относительно этой системы.
2) Выбрать координатные оси, записать закон сохранения импульса в скалярной форме двумя уравнениями:
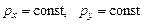 .
.
Если импульсы всех тел системы направлены вдоль одной прямой, то, выбрав координатную ось, направленную вдоль этой прямой, сразу записывают закон сохранения импульса в скалярной форме:
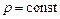 ,
,
где p - сумма проекций импульсов всех тел системы.
3) Если число неизвестных больше числа составленных уравнений, нужно добавить к ним уравнения, связывающие кинематические величины, и решить полученную систему уравнении.
При решении ряда задач, когда нас интересует лишь относительное движение частиц внутри системы, а не ее движение как целого, целесообразно пользоваться системой отсчета, в которой центр масс системы покоится
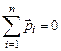 .
.
Систему отсчета, жестко связанную с центром масс и перемещающуюся поступательно по отношению к инерциальным системам, называют системой центра масс. Центр масс любой системы частиц движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы. Положение центра масс относительно начала данной системы отсчета характеризуется радиус-вектором
 ,
,
где 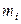 и
и 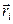 - масса и радиус-вектор i -ой частицы,
- масса и радиус-вектор i -ой частицы, 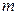 - масса всей системы.
- масса всей системы.
Скорость центра масс определяется как
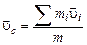 .
.
Импульс системы равен произведению массы системы на скорость ее центра масс
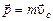 .
.
Решение задач
4.1. Космический корабль перед отделением последней ступени ракеты-носителя двигался со скоростью  . После отбрасывания последней ступени, его скорость стала равной
. После отбрасывания последней ступени, его скорость стала равной  , при этом отделившаяся ступень удаляется относительно корабля со скоростью
, при этом отделившаяся ступень удаляется относительно корабля со скоростью 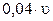 . Какова масса
. Какова масса 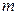 отделившейся ступени, если масса корабля после отделения ступени равна
отделившейся ступени, если масса корабля после отделения ступени равна 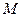 .
.
|
|
|
Решение. Космический корабль двигался со скоростью  относительно Земли. Поскольку скорость ракеты постоянна, рассматриваемая система является замкнутой. Поэтому согласно закону сохранения импульса
относительно Земли. Поскольку скорость ракеты постоянна, рассматриваемая система является замкнутой. Поэтому согласно закону сохранения импульса
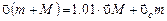 ,
,
где 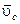 - скорость отделившейся ступени в рассматриваемой системе отсчета. Согласно правилу сложения скоростей
- скорость отделившейся ступени в рассматриваемой системе отсчета. Согласно правилу сложения скоростей
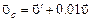 ,
,
По условию задачи 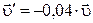 , поэтому после подстановки получим
, поэтому после подстановки получим
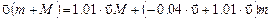 .
.
Решив полученное уравнение, получим массу отделившейся ступени
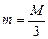 .
.
4.2. Две одинаковые тележки 1 и 2, на каждой из которых находится по человеку, движутся без трения по инерции навстречу друг другу по параллельным рельсам. Когда тележки поравнялись, с каждой из них на другую прыгнул человек в направлении перпендикулярном к движению тележек. В результате тележка 1 остановилась, а скорость тележки 2 стала  . Найти первоначальные скорости тележек
. Найти первоначальные скорости тележек 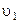 и
и 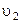 , если масса каждой тележки (без человека) M, а масса каждого человека m.
, если масса каждой тележки (без человека) M, а масса каждого человека m.
Решение. Импульс всей системы в результате прыжков людей, не изменится, поэтому
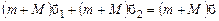 .
.
Направим ось X в направлении движения 1 -ой тележки и запишем последнее выражение в проекциях на эту ось:
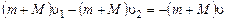 ,
,
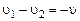 .
.
Импульс 1 -ой тележки в конечном состоянии запишется как:
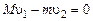 .
.
Из этих двух уравнений, найдем первоначальные скорости 1 -ойи 2 -ой тележек:
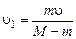 ,
, 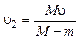 .
.
4.3. Частица 1 столкнулась с частицей 2, в результате чего возникла новая частица. Найти ее скорость  и модуль
и модуль  , если масса у частицы 2 в
, если масса у частицы 2 в 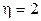 раза больше, чем у частицы 1, а их скорости перед столкновением равны
раза больше, чем у частицы 1, а их скорости перед столкновением равны 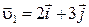 и
и 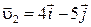 , где компоненты скорости даны в СИ.
, где компоненты скорости даны в СИ.
Решение. Рассматриваемая система состоит из 2-х частиц. Силы, возникающие при ударе, будут внутренними, поэтому рассматриваемая система является замкнутой. Согласно закону сохранения импульса, импульс такой системы в результате столкновения не изменится:
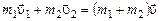 .
.
Разделим записанное уравнение на 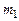 и, учитывая, что
и, учитывая, что 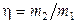 , получим:
, получим:
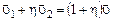 ,
,
откуда 
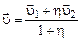 .
.
Подставив в полученное выражение 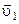 и
и 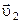 , найдем вектор скорости образовавшейся частицы:
, найдем вектор скорости образовавшейся частицы:
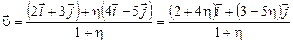 ,
,
с учетом того, что 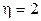 , получим:
, получим:
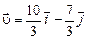 .
.
Модуль вектора скорости равен
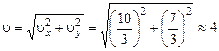 м/с.
м/с.
|
|
|
4.4. В результате взрыва камень разлетается на три части. Два осколка движутся под прямым углом друг к другу: первый массой 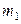 - со скоростью
- со скоростью 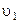 , второй осколок массой
, второй осколок массой 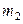 - со скоростью
- со скоростью 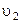 . Третий осколок отлетает со скоростью
. Третий осколок отлетает со скоростью 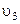 . Какова его масса и в каком направлении он движется.
. Какова его масса и в каком направлении он движется.
Решение. I способ решения. Рассматриваемая система состоит их трех осколков. Внешней силой является сила тяжести. Но так как время разрыва камня очень мало, импульс внешней силы можно считать равным нулю, а силы, возникающие при взрыве, будут внутренними, поэтому рассматриваемая система является замкнутой. Следовательно, импульс камня до разрыва равен сумме импульсов осколков после разрыва:
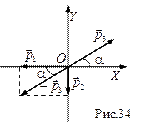
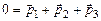 .
.
Зададим направление осей OX и OY как показано на рис.34. Зная направления векторов 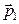 и
и 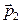 , найдем построением вектор
, найдем построением вектор 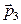 :
:
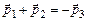 .
.
Как видно из рисунка
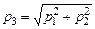 и
и  .
.
Учитывая, что 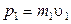 ,
,  и
и 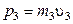 , найдем массу третьего осколка:
, найдем массу третьего осколка:
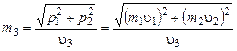 .
.
Угол, который образует вектор 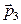 с осью OX,равен
с осью OX,равен
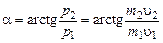 .
.
II способ решения. Согласно закону сохранения импульса:
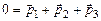 .
.
Составим уравнения в проекциях на оси OX и OY:
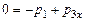 и
и 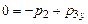 ,
,
где 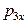 и
и 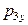 - проекции вектора
- проекции вектора 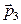 на оси OX и OY соответственно. Из последних двух выражений найдем
на оси OX и OY соответственно. Из последних двух выражений найдем 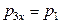 и
и 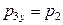 .
.
Модуль вектора 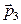 равен:
равен:
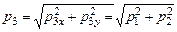 .
.
Как и при решении задачи первым способом, найдем массу третьего осколка:
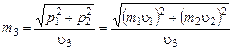 .
.
Вектор 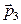 образует с осью OX угол
образует с осью OX угол
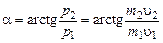 .
.
4.5*. Система состоит из двух шариков массами 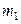 и
и 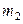 , которые соединены между собой невесомой пружинкой. В момент
, которые соединены между собой невесомой пружинкой. В момент 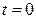 шарикам сообщили скорости
шарикам сообщили скорости 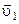 и
и 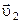 , после чего система начала двигаться в однородном поле тяжести Земли. Пренебрегая сопротивлением воздуха, найти зависимости от времени импульса этой системы в процессе движения и радиус-вектора ее центра масс относительно его начального положения.
, после чего система начала двигаться в однородном поле тяжести Земли. Пренебрегая сопротивлением воздуха, найти зависимости от времени импульса этой системы в процессе движения и радиус-вектора ее центра масс относительно его начального положения.
Решение. а) Запишем уравнение движения системы (второй закон
Ньютона) в общем виде:
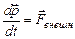 .
.
Система движется в однородном поле тяжести Земли, поэтому сила тяжести будет единственной внешней силой, действующей на систему:
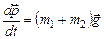 .
.
Разделив переменные, приведем уравнение к виду, удобному для интегрирования:
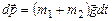 .
.
Проинтегрировав левую часть этого выражения от 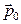 до
до 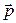 , а правую от 0 до t, и учитывая, что начальный импульс системы равен
, а правую от 0 до t, и учитывая, что начальный импульс системы равен 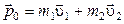 , найдем зависимость от времени импульса системы в процессе движения:
, найдем зависимость от времени импульса системы в процессе движения:
|
|
|
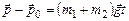
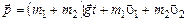 .
.
б) Радиус-вектор центра масс в произвольный момент времени относительно его начального положения равен:
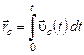 .
.
Найдем зависимость 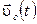 , учитывая,что импульс системы равен произведению массы системы на скорость ее центра масс
, учитывая,что импульс системы равен произведению массы системы на скорость ее центра масс 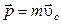 и
и 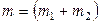 :
:
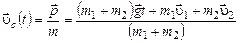 .
.
Подставив значение 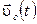 в уравнение для
в уравнение для 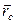 и проведя интегрирование, получим искомую величину:
и проведя интегрирование, получим искомую величину:
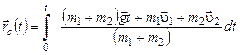 ,
,
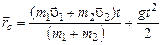 .
.
4.6. Цепочка массы 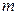 и длины
и длины 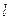 висит на нити, касаясь поверхности стола своим нижним концом. После пережигания нити цепочка упала на стол. Найти полный импульс, который она передала столу.
висит на нити, касаясь поверхности стола своим нижним концом. После пережигания нити цепочка упала на стол. Найти полный импульс, который она передала столу.
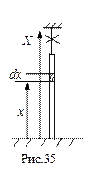 Решение. Выберем малый элемент цепочки длиной
Решение. Выберем малый элемент цепочки длиной 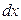 на высоте x (рис.35).
на высоте x (рис.35).
Рассматривая свободное падение этого элемента, найдем его скорость у поверхности стола:
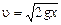 .
.
Масса элемента цепочки длиной 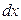 равна
равна
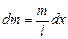 ,
,
а импульс, переданный столу:
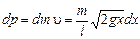 .
.
Проинтегрировав левую часть этого выражения от 0до p, а правую от 0 до l, найдем полный импульс, переданный цепочкой столу:
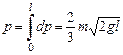 .
.
4.7*. Ракета, масса которой в начальный момент времени 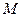 , запущена вертикально вверх. Относительная скорость выхода продуктов сгорания
, запущена вертикально вверх. Относительная скорость выхода продуктов сгорания 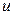 , расход горючего
, расход горючего 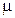 (где
(где 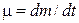 - масса горючего, сжигаемого в единицу времени). Пренебрегая сопротивлением воздуха, определите ускорение ракеты
- масса горючего, сжигаемого в единицу времени). Пренебрегая сопротивлением воздуха, определите ускорение ракеты 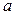 через время
через время 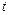 после начала ее движения. Поле силы тяжести считать однородным.
после начала ее движения. Поле силы тяжести считать однородным.
 Решение. Уравнение движения тела переменной массы (уравнение Мещерского) имеет вид:
Решение. Уравнение движения тела переменной массы (уравнение Мещерского) имеет вид:
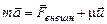 .
.
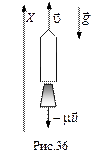
Учитывая, что ракета движется в однородном поле тяжести Земли, и сила тяжести - единственная внешняя сила, действующая на ракету, уравнение движения в проекциях на вертикальную ось X с положительным направлением вверх примет вид (рис.36):
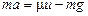 .
.
Масса ракеты через время 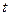 после начала ее движения равна
после начала ее движения равна 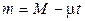 , а ускорение ракеты:
, а ускорение ракеты:
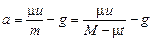 .
.
4.8*. Ракета движется в отсутствие внешних сил, выпуская непрерывную струю газа со скоростью 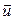 , постоянной относительно ракеты. Найти скорость ракеты
, постоянной относительно ракеты. Найти скорость ракеты  в момент, когда ее масса равна
в момент, когда ее масса равна 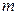 , если в начальный момент времени она имела массу
, если в начальный момент времени она имела массу 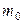 и ее скорость была равна нулю.
и ее скорость была равна нулю.
Решение. Запишем уравнение движения тела переменной массы (уравнение Мещерского):
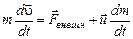 .
.
Учитывая, что по условию 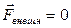 , преобразуем уравнение к виду удобному для интегрирования:
, преобразуем уравнение к виду удобному для интегрирования:
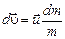 .
.
Проинтегрировав левую часть этого выражения от 0до  , а правую от
, а правую от 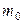 до
до 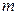 , найдем искомую скорость ракеты:
, найдем искомую скорость ракеты:
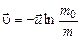 .
.
Знак «–» показывает, что скорость ракеты 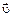 противоположена направлению скорости
противоположена направлению скорости 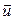 струи газа. По условию задачи
струи газа. По условию задачи 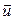 - const, поэтому скорость ракеты не зависит от времени сгорания топлива, а определяется только отношением начальной и конечной масс ракеты.
- const, поэтому скорость ракеты не зависит от времени сгорания топлива, а определяется только отношением начальной и конечной масс ракеты.
|
|
|


