Закон обратного отношения между объемами и содержаниями понятий

 

В этом законе речь идет о понятиях, находящихся в родо­видовых отношениях. Объем одного понятия может входить в объем другого понятия и составлять при этом лишь его часть. Например, объем понятия «хищная рыба» целиком входит в объ­ем другого, более широкого по объему понятия «рыба» (состав­ляет часть объема понятия «рыба»). При этом содержание пер­вого понятия оказывается шире, богаче (содержит больше при­знаков), чем содержание второго. На основе обобщения такого рода примеров можно сформулировать следующий закон: чем шире объем понятия, тем уже его содержание, и наоборот. Этот закон называется законом обратного отношения между объе­мами и содержаниями понятий. Он указывает на то, что чем меньше информации о предметах, заключенной в понятии, тем шире класс предметов и неопределеннее его состав (например, «водопад»), и наоборот, чем больше информации в понятии, например, «крупный водопад» или «крупный водопад в Канаде»), тем уже и определеннее круг его предметов, или даже мыслит­ся только один предмет [8, 15, 55].

Отношения между понятиями

 

Предметы мира находятся друг с другом во взаимосвязи и взаимообусловленности. Поэтому и понятия, отражающие эти предметы, также находятся в определенных условиях. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (например, «поэма» и «колодец»; «невоспитанность» и «радуга»), остальные понятия называются сравнимыми.

Сравнимые понятия делятся по объему на совместимые (объемы этих понятий совпадают полностью или частично) и несовместимые (их объемы не имеют общих элементов).

Типы совместимости: равнозначность (тождество), перекрещивание, подчинение (отношение рода и вида).

Отношения между понятиями изображают с помощью кру­говых схем (кругов Эйлера), где каждый круг обозначает объ­ем понятия. Кругом изображается и единичное понятие. Например: учебные принадлежности (А), ручка (В), тетрадь (С), учебник (D), учебник «Логика» (Е), компьютер (F) (рис. 2.2.1).

 

 

 

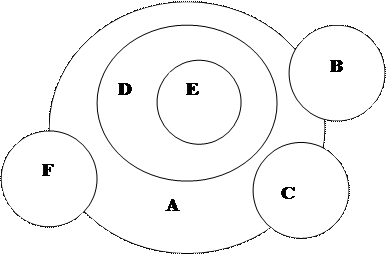Рис. 2.2.1. Пример отношений между понятиями с помощью кру­говых схем (кругов Эйлера)

 

Равнозначными, или тождественными, называются поня­тия, которые, различаясь содержанием, имеют равные объемы. В них мыслится или одноэлементный класс, или один и тот же класс предметов, состоящий более чем из одного элемента. При­меры равнозначных понятий: 1) «река Нил» и «самая длинная река в мире»; 2) «автор романа «Красное и черное», «автор романа «Пармская обитель»; 3) «равносторонний прямоугольник»: «квад­рат»; «равноугольный ромб». Объемы тождественных понятий изображаются кругами, полностью совпадающими.

Определение понятий

Определение (дефиниция) (от лат. definitio - определение) понятия - логическая операция раскрытия содержания поня­тия или значения термина.

С помощью определения понятий мы в явной форме раскрыва­ем содержание понятия и тем самым отличаем круг определяе­мых предметов от других предметов.

Давая такие определения, мы отличаем науку информатику от других наук, а правильные дроби от всех других дробей, напри­мер, неправильных или десятичных.

Приведем еще несколько определений понятий, взятых из школьных учебников, которые принадлежат к двум различным видам определений (реальным и номинальным). «Зоология — это наука о животных, об их разнообразии, строении, поведении, раз­множении, развитии, происхождении, а также о значении в при­роде и жизни человека» (1); «Слово «зоология» происходит от двух греческих слов: «зоон» — животное и «логос» — слово, учение, нау­ка» (2); «Число, которое показывает, во сколько раз умень­шены (увеличены) настоящие расстояния на чертеже, называ­ется масштабом» (3).

Понятие, содержание которого надо раскрыть, называется оп­ределяемым понятием (definiedum, сокращенно Dfd), а то по­нятие, посредством которого оно определяется, называется опре­деляющим понятием (definience, сокращенно Dfn). Правиль­ное определение устанавливает между ними отношение равен­ства (эквивалентности).

Определения делятся неявные и неявные. В явных определе­ниях даны определяемое понятие и определяющее, объемы ко­торых равны, т. е. Dfd ≡ Dfn. К их числу относится самый распространенный способ определения через ближайший род и видовое отличие, где формулируются существенные признаки определяемого понятия. Например: «Барометр — прибор для из­мерения атмосферного давления»; «Треугольник — многоуголь­ник с тремя сторонами»; «Гротеск — способ сатирического изо­бражения жизни, отличающийся резким преувеличением, соче­танием реального и фантастического».

Признак, указывающий на тот круг предметов, из числа ко­торых нужно выделить определяемое множество предметов, на­зывается родовым признаком, или родом. В приведенных выше примерах это «прибор», «многоугольник», «способ сатирическо­го изображения жизни». Признаки, при помощи которых выделя­ется определяемое множество предметов из числа предметов, соответствующих родовому понятию, называется видовым от­личием (их может быть один или несколько).

Разновидностью определения через род и видовое отличие яв­ляется генетическое определение, в котором указывается способ образования только данного предмета. Например: «Кислотами называются сложные вещества, образующиеся из кислотных остатков и атомов водорода, способных замещаться атомами металлов или обмениваться на них»; «Коррозия металлов — это окислительно-восстановительный процесс, образующийся в ре­зультате окисления атомов металла». Много генетических оп­ределений в математике, к их числу относятся такие, как «ци­линдр вращения», «конус вращения».

Определения через ближайший род и видовое отличие и ге­нетические определения входят в класс реальных определений, ибо они определяют само понятие, например, «информатика», «треугольник», «кислота» и др. К явным относятся и номиналь­ные определения. Последние дают определение термина, кото­рый обозначает понятие, или вводят знаки, заменяющие поня­тие (обычно в свой состав они включают слово «называется»). Они часто встречаются в математике. Например: «Конус назы­вается круговым, если основание его - круг»; «Прямая, соединя­ющая вершину конуса и центр основания, называется осью кону­са». Номинальными определениями, вводящими знаки, являются следующие: «g- ускорение свободно падающего тела», «m - мас­са тела», «знак v обозначает дизъюнкцию» и т. п. В при­веденных выше примерах определения (1), (3) - реальные, а опре­деления (2), (4) и (5) - номинальные.

Чтобы определение было правильным, надо соблюдать следующие правила.

Правила явного определения. Ошибки, возможные в определении.

1. Определение должно быть соразмерным, т. е. объем определяющего понятия должен быть равен объему определяе­мого понятия: Dfd ≡ Dfn.

Это правило часто нарушается, в результате чего в определе­нии возникают логические ошибки. Типы этих логических ошибок:

А. Широкое определение, когда определяющее понятие по объ­ему шире, чем определяемое понятие Dfd < Dfn. Такая ошибка содержится в следующих определениях: «Гравитация — это взаи­модействие двух материальных тел»; «Костер — источник тепла».

Понятие «окружность» неправильно определяется так: «Это фи­гура, которая описывается движущимся концом отрезка, когда другой его конец закреплен, или фигура, которая образована дви­жущимся концом циркуля». С помощью этого определения нельзя отличить понятие «окружность» от понятия «дуга», так как не указано, что окружность - это кривая замкнутая линия.

Приведем пример из истории философии. Древнегреческий философ Платон дал такое определение понятия «человек»: «Человек — это двуногое животное без перьев». На лекцию Пла­тона в Академию другой философ Диоген с целью доказать ло­гическую ошибку Платона в определении понятия принес ощи­панного петуха и выпустил его в аудиторию со словами: «Вот человек Платона». Утверждают, что Платон признал свою ошиб­ку и уточнил первоначальное определение: «Человек - это дву­ногое животное без перьев с широкими ногтями».

Б. Узкое определение, когда определяющее понятие по объе­му уже, чем определяемое понятие: Dfd > Dfn. Например: «Вер­шина — самая высокая часть холма», однако и у горы есть верши­на. Другое: «Совесть — это осознание человеком ответственно­сти перед самим собой за свои действия и поступки» (а перед обществом?).

В. Определение в одном отношении широкое, в другом — узкое. Например: «Ящик — тара для хранения овощей». С одной стороны, это широкое определение, так как тарой для хранения овощей может быть мешок и контейнер и т. д., с другой сторо­ны, это узкое определение, так как ящик пригоден для хранения и цемента, и песка, а не только овощей.

2. Определение не должно содержать круга. Круг возникает тогда, когда определяемое понятие и определяющее понятие выражаются одно через другое. В определении «Вращение есть движение вокруг своей оси» будет допущен круг, если до этого понятие «ось» было определено через понятие «вращение» («Ось - это прямая, вокруг которой происходит вращение»).

Круг возникает и тогда, когда определяемое понятие характери­зуется через него же, но лишь выражено иными словами, или ко­гда определяемое понятие включается в определяющее понятие в качестве его части. Такие определения носят название тавто­логий. Например: «Смешное — это то, что вызывает смех»; «Сверхпроводник — вещество, обнаруживающее явление сверх­проводимости»; «Количество — характеристика предмета с его количественной стороны».

Логически некорректным является употребление таких, напри­мер, тавтологий, как «масляное масло», «трудоемкий труд», «пору­ченное поручение», «прогрессирующий прогресс», «заданная за­дача», «изобрету изобретение», «поиграем в игру», «памятный су­венир», «подытожим итоги», «старый старик» и др. Иногда можно встретить выражения типа «Закон есть закон», «Жизнь есть жизнь» и т.д., которые представляют собой прием усиления, а не сообще­ния в предикате какой-то информации о субъекте, так как субъект и предикат тождественны. Такие выражения не претендуют на оп­ределение соответствующего понятия: «закон», «жизнь» или др.

3. Определение должно быть четким, ясным. Это правило означает, что смысл и объем понятий, входящих в Dfn, должен быть ясным и определенным. Определения понятий должны быть свободными от двусмысленности; не допускается подмена их метафорами, сравнениями и т. д.

Не являются правильными определениями следующие суждения: «Лень – мать всех пороков»; «Природа — это наука, способствующая пониманию вопросов, относящихся к духовной истине» (Р. Эмерсон); «Упрямство — порок ума»; «Такт — это разум сердца» (К. Гуцков); «Неблагодарность — род слабости» (И. В. Гете). Эти истинные суждения представляют собой интересные метафоры, поучительные афоризмы, которыми мы пользуемся при передаче информации, но они не являются опре­делениями понятий.

 

Неявные определения

 

В отличие от явных определений, имеющих структуру Dfd ≡ Dfn, в неявных определениях на место Dfn просто подставляется кон­текст, или набор аксиом, или описание способа построения опреде­ляемого объекта. Выделяют, по крайней мере, три вида.

Контекстуальное определение позволяет выяснить содержа­ние незнакомого слова, выражающего понятие, через контекст, не прибегая к словарю для перевода (если текст на иностранном язы­ке) или к толковому словарю (если текст дан на родном языке). Так, контекст помогает выяснить, что «заткнуть за пояс» означает «превзойти кого-либо»: «Стукнуло ребяткам десять лет, отдала их мать в науку: скоро они научились грамоте и боярских и купечес­ких детей за пояс заткнули —никто лучше их не сумеет ни про­честь, ни написать, ни ответу дать» (А. Афанасьев); «Стареешь ты, Фишка. – Старею? — удивился тот и хвастливо сказал: – Я еще молодого за пояс заткну!» (Г. Марков).

Понятие «золотая середина» — образ поведения, при котором избегают крайностей, рискованных решений, — отражено в следу­ющих контекстах: «Все б — в крайностях бродить уму, а середи­на золотая все не давалася ему!» (А. Блок); «Кареты разъеха­лись. Мать даже всплакнула: — Всегда вы умудряетесь дово­дить страсти до критических крайностей. Ах, Фике, как хорошо знать золотую середину...» (В. Пикуль).

Индуктивные определения — такие, в которых определяе­мый термин используется в выражении понятия, которое ему приписывается в качестве его смысла. Примером индуктивно­го определения является определение понятия «натуральное число» с использованием самого термина «натуральное число»:

1. 1— натуральное число.

2. Если п — натуральное число, то п + 1 — натуральное число.

3.Никаких натуральных чисел, кроме указанных в пунктах 1 и 2, нет.

С помощью этого индуктивного определения получается нату­ральный ряд чисел: 1, 2, 3, 4... Таков алгоритм построения ряда натуральных чисел.

Определение через аксиомы

 

В современной математике и в математической логике ши­роко применяется так называемый аксиоматический метод. При­ведем пример. Пусть дана система каких-то элементов (обоз­начаемых х, у, z...), и между ними установлено отношение, вы­ражаемое термином «предшествует». Не определяя ни самих объектов, ни отношения «предшествует», мы высказываем для них следующие утверждения (аксиомы):

1. Никакой объект не предшествует сам себе.

2. Если х предшествует у, a y предшествует z, то х предшествует z.

Так с помощью двух аксиом определены системы объектов вида «х предшествует у». Например, пусть объектами c, у, z являются люди, а отношение между х и у представляет собой «х старше у». Тогда выполняются утверждения 1 и 2. Если объ­екты х, у, z —действительные числа, а отношение «х предшест­вует у» представляет собой «х меньше у», то утверждения 1 и 2 также выполняются. Утверждения (т. е. аксиомы) 1 и 2 опреде­ляют системы объектов с одним отношением [32].

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: