Метод наименьших квадратов.

Метод наименьших квадратов

Наш мир не идеален, ни в чем нельзя быть уверенным с абсолютной точностью. Кто помнит лабораторные работы по физике, тот должен знать, что измерение какой-либо физической величины обычно проводят несколько раз при различных условиях, а найденный результат записывают в виде 20,3±2,3. Это необходимо для того, чтобы нейтрализовать погрешности приборов, трясущиеся руки экспериментатора, вспышки на солнце и так далее.

Метод наименьших квадратов (далее МНК), о котором пойдет речь в этой статье, является одним из способов противостоять ошибкам измерений.

Общая формулировка метода выглядит так:

Пусть имеется система уравнений:

Здесь f(x) эта некая функция, конкретный вид которой не известен, известен лишь ее общий вид, например известно что это прямая, или многочлен, или синусоида и так далее. МНК позволяет зная общий вид функции найти ее конкретный вид (коэффициенты) который наилучшим образом вписывается в экспериментальные данные.

Особенностью МНК является то, что число уравнений превышает число неизвестных коэффициентов в функции f(x). Таким образом, в общем случае точного решения системы не существует.

Обратите внимание, что система решается не относительно xn, а относительно неизвестных коэффициентов функции f(x).

Основная идея МНК состоит в том, чтобы при нахождении конкретного вида функции минимизировать сумму квадратов ошибок во всех исходных уравнениях.

Иными словами нужно свести к минимуму функцию:

Может возникнуть вопрос почему сумма квадратов? Дело в том, что во-первых, квадрат любого числа всегда неотрицателен, и следовательно сумма квадратов всегда не отрицательна, т.е. ограничена снизу, а следовательно у нее есть минимум; во-вторых, при нахождении минимальной суммы квадратов мы уменьшаем максимальную ошибку.

Согласитесь, что иметь в двух точках ошибку в 5 единиц, лучше, чем в первой точке иметь нулевое отклонение, зато во второй точке иметь отклонение 10. Сумма отклонений в обоих случаях будет одинаковой, а вот сумма квадратов отклонений в первом случае будет меньше.

Коэффициент корреляции и его основные свойства, оценка достоверности полученных моделей.

2. Коэффициент корреляции.

Для характеристики корреляционной зависимости между случайными величинами ведем понятие коэффициента корреляции.

Если Х и У являются независимыми случайными величинами, то М(ХУ) =М(Х)М(У). Если же Х и У зависимые, то М(ХУ) и М(Х)М(У) не равны.

За меру зависимости Х и У принята безразмерная величина r, определяемая соотношением

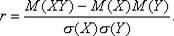
r называется коэффициентом корреляции.

Случайные величины Х и У называются некоррелированными, если r =0, и коррелированными, если r≠ 0.

Свойства коэффициента корреляции:

1. Если Х и У независимые СВ, то r =0;

2. -1< r <1.При этом, если |r| =1, то между Х и У функциональная, а именно линейная зависимость;

3. r характеризует относительную величину отклонения М(ХУ) от М(Х)М(У), и т.к. отклонение имеет место только для зависимых величин, то r характеризует тесноту зависимости.

Коэффициент корреляции — это мера взаимосвязи измеренных явлений. На самом примитивном уровне его можно рассматривать как меру совпадения двух рядов чисел. Любой коэффициент корреляции изменяется в пределах от -1 до +1. Отрицательные значения говорят про обратнопропорциональную взаимосвязь, положительные о прямопропорциональной. Полученный коэффициент необходимо сравнивать с критическим табличным.