 |
Моделирование нелинейных процессов, построение моделей процессов, описываемых полулогарифмической, степенной и экспоненциальной зависимостью.
|
|
|
|
Модель нелинейной парной регрессии.
Соотношение между социально экономическими явлениями и процессами не всегда можно выразить линейными функциями, потому что при этом могут возникать большие ошибки.
Примеры нелинейных функций:
· Производственные функции. Зависимости между объемом произведенной продукции и основными факторами производства — трудом, капиталом и т.п;
· Функции спроса. Зависимость между спросом на товары или услуги и их ценами или доходом и др.
Для оценки параметров нелинейных моделей используются два подхода:
1. Этот подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.
2. Методы нелинейной оптимизации на основе исходных переменных применяется в том случае, когда подобрать соответствующее линеаризующее преобразование не удается.
Для того что бы линеаризовать модель в рамках первого подхода можно использовать как модели, не линейные по переменным, так и не линейные по параметрам.
Если модель нелинейная по переменным, то введением новых переменных ее можно свести к линейной модели, для оценки параметров которой использовать обычный метод наименьших квадратов.
Так, например, если нам необходимо оценить параметры регрессионной модели
то, вводя новые переменные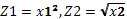 
= получим линейную модель
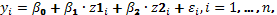
параметры которой находятся обычным методом наименьших квадратов.
Следует, однако, отметить и недостаток такой замены переменных, связанный с тем, что вектор оценок Ь получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации сумму квадратов отклонений для преобразованных переменных, что не одно и то же. В связи с этим необходимо определенное уточнение полученных оценок.
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. В известном учебнике по эконометрике [261 все нелинейные регрессии делятся на два класса:
1) регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам:
полиномы разных степеней
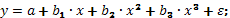
равносторонняя гипербола
;
|
|
|
2) регрессии, нелинейные по оцениваемым параметрам:
степенная 
показательная 
∙ε
экспоненциальная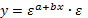 
Мультипликативная или степенная модель имеет проблему нелинейности модели по параметрам, так как непосредственное применение метода наименьших квадратов для их оценивания невозможно.
Оценку параметров нелинейной регрессии по объясняющим переменным можно провести методом наименьших квадратов, так как эти функции линейны по параметрам.
Для любого многочлена к-го порядка
,
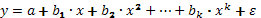с помощью замены переменных 
получим линейную модель множественной регрессии
.
из этого следует, что полином любого порядка сводится к линейной регрессии с её методами оценивания и проверки гипотез.
Теперь рассмотрим применение МНК для случая, когда теоретическая линия описывается многочленом второго порядка.
Применение МНК для оценки параметров второй степени приводит к следующей системе нормальных уравнений:
Решать мы её будем с помощью метода Крамера и рассмотрим, как получается решение (коэффициенты регрессии): 
;
где 
— определитель системы;
а,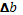 
, с — определители, полученные заменой соответствующего столбца на столбец свободных членов.
Чаще всего исследователь имеет дело с отдельными сегментами, а не с полной параболической формой а не симметричной кривой многочлена второй степени, который не всегда может быть пригоден в данных исследованиях. Данную ситуацию рассмотрим в примере данных таблицы №1.
Пример 1. Пусть нас интересует построение регрессионной зависимости между переменной х — количество внесённых минеральных удобрений (центнеров на 1 га) переменной у — урожайностью некоторых злаковых с одного гектара.
Таблица 1
|
|
|
| Внесено минеральных удобрений ц/га, х | Урожайность, ц с 1 га, y | 
| 
| 
| y∙x | y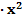 
| 
| |
| 6,171 | ||||||||
| 8,516 | ||||||||
| 10,63 | ||||||||
| 256 | 11,91 | |||||||
| 625 | 12,97 | |||||||
| Итого |
По данным таблицы система нормальных уравнений будет иметь вид:
Решая её методом Крамера, получим =700, а=2380, 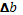=2090, 
=-150. Следует а=3,6; b=2,986; с=-0,216, тогда уравнение многочлена второй степени примет вид
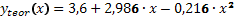
Среди класса нелинейных функций следует назвать хорошо известную в эконометрике равностороннюю гиперболу
.
Она может быть использована не только для характеристики связи удельных расходов сырья, материалов, топлива с объёмом выпускаемой продукции, времени обращения товаров от величины товарооборота, т.е. на микро уровне, но и на макро уровне. Классическим её примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы х и процентом прироста заработной платы у.
А.В. Филлипс, установил обратную зависимость процента прироста зарплаты от уровня безработицы: y=a+b/x+ε.
Для того, что бы получить равностороннюю гиперболу нужно получть линейное уравнение регрессии y=a+b*z+ε, при помощью замены z=1/x.
А что бы оценить параметры, применим МНК и получим следующую систему нормальных уравнений:
При b>0 имеем обратную зависимость, которая при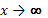 
характеризуется нижней асимптотой. Так, для кривой Филлипса y(x)=0,00679+0,1862/x величина параметра а =0,0679, означает, что с ростом уровня безработицы темп прироста зарплаты в пределе стремится к 0.
При b<0 имеем медленно повышающуюся функцию с верхней асимптотой а при 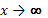. Примером может служить взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (или доходов). Э. Энгель на основе своих исследований сформулировал закономерность с ростом дохода (х) доля доходов, расходуемых на продовольствие, уменьшается. Соответственно, доля расходов, расходуемых на непродовольственные товары (у), увеличивается до а:y=a-b/x.
|
|
|
Уоркинг и С. Лизер для описания кривой Энгеля использовали полулогарифмическую кривую y=a+b∙ln(x)+ε. С помощью замены z=ln(х), получим линейное уравнение регрессии y=a+b∙z+ε, дляоценки параметров которого применим МНК и получим следующую систему нормальных уравнений:
Возможны и иные модели, нелинейные по объясняющим переменным, например, y=a+b* 
. Соответственно, система нормальных уравнений будет иметь вид:
Приступим к рассмотрению моделей нелинейных по оцениваемым параметрам. Эти модели подразделяются на два типа:
1. Нелинейные модели внутренне линейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду.
2. Нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она не может быть сведена к линейной функции.
Данные модели можно рассмотреть на примере в эконометрических исследованиях при изучении эластичности спроса от цены широко используется степенная функция:
,
где D — спрашиваемое количество; Р-цена; ε-случайная ошибка.
Эту модель можно считать внутренне линейной, так как логарифмирование данного уравнения по основанию е (е = 2,718281...) приводит его к линейному виду:
А к последнему выражению можно применить МИК. Следующая модель 
-внутренне нелинейна, так как её невозможно превратить в линейный вид. Модель 
тоже внутренне нелинейна. Для оценки параметров внутренне нелинейных моделей используют итеративные процедуры.
|
|
|
