 |
2.2.3.4 Диаграмма плавкости, компоненты которой неограниченно растворимы в жидком и полностью не растворимы друг в друге в твердом состояниях
|
|
|
|
2. 2. 3. 4 Диаграмма плавкости, компоненты которой неограниченно растворимы в жидком и полностью не растворимы друг в друге в твердом состояниях
На подобных диаграммах состояния признаком полной нерастворимости твердых фаз является наличие точки эвтектики E. Эвтектическая смесь – мелкокристаллическая смесь. Более крупные кристаллы смеси отвечают компоненту, кристаллизация которого начинается раньше.
На диаграмме (рисунок 2. 28) имеется только одна гомогенная область – область двухкомпонентного расплава. Остальные области – гетерогенные, двухфазные (см. подписи к рисунку 2. 28).
| Tfus. B |
| I II III E IV |
| Tfus. А |
Области:
I – двухкомпонентный расплав A и B;
II – двухкомпонентный расплав A и B и кристаллы А;
III – двухкомпонентный расплав A и B и кристаллы В;
IV - кристаллы А и кристаллы В
Рисунок 2. 28 – Диаграмма состояния А – B, компоненты которой неограниченно
растворимы в жидком и полностью не растворимы друг в друге в твердом состояниях
2. 2. 3. 5 Диаграмма плавкости, компоненты которой ограниченно растворимы друг в друге в твердом состоянии
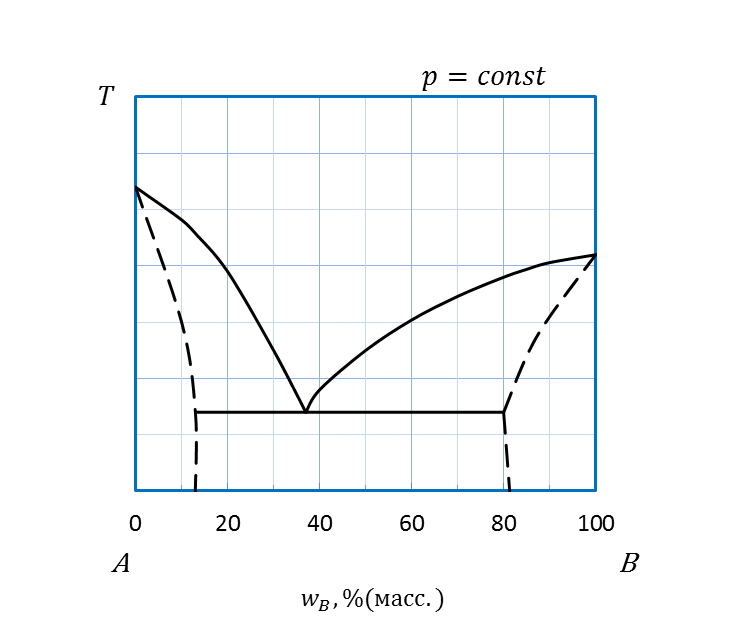
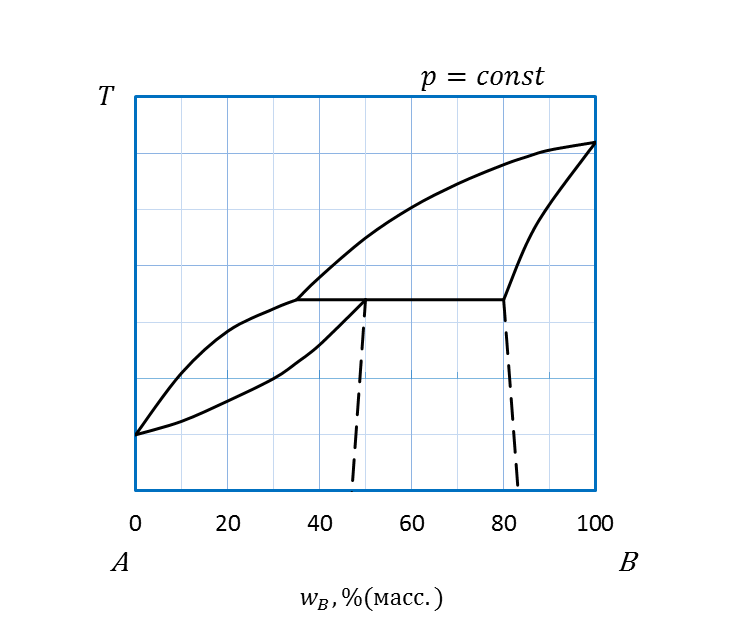Ограниченная растворимость в твердом состоянии предполагает появление на диаграммах состояния областей как растворимости в твердом агрегатном состоянии (области IV и V, рисунок 2. 29), так и области нерастворимости (область VI). В гомогенных областях растворимости кристаллизуются твердые растворы внедрения А в В (область V) и В в А (область IV), соответственно. В областях II и III в равновесии с двухкомпонентным расплавом A и B сосуществует твердый раствор В в А или твердый раствор А в В, соответственно.
|
|
|
| a б |
| Tfus. А |
| Tfus. А |
| Tfus. B |
| Tfus. B |
| I II III IV V E VI |
| I III P II V IV VI |
Области:
I –двухкомпонентный расплав A и B;
II – двухкомпонентный расплав A и B и твердый раствор В в А;
III – двухкомпонентный расплав A и B и твердый раствор А в В;
IV – твердый раствор В в А;
V – твердый раствор А в В;
VI – твердый раствор А в В и твердый раствор В в А.
Тип: а- эвтектоидный; б– перитектоидный
Рисунок 2. 29 – Диаграммы состояния А – B, компоненты которых неограниченно
растворимы в жидком и ограниченно растворимы друг в друге в твердом состояниях
Частным случаем диаграмм с ограниченной растворимостью являются диаграммы перитектоидного типа, т. е. с точкой перитектики P на кривой ликвидуса. В таких диаграммах расплав состава P обогащен по сравнению с составами твердых растворов легкоплавящимся компонентом. Распределение фаз остается таким же, как и на диаграммах эвтектоидного типа (с точкой эвтектики E). В точке перитектики происходит перитектическое превращение кристаллов одного типа твердого раствора в другой.
2. 2. 3. 6 Диаграмма плавкости, компоненты которой образуют между собой в твердом состоянии химическое соединение, плавящееся без разложения
Температуре плавления устойчивого химического соединения отвечает максимум на кривой ликвидуса – точка D – точка дистектики (рисунок 2. 30).
|
|
|
| I D II III IV V VI E VII |
| Tfus. B |
| Tfus. А |
Области:
I – двухкомпонентный расплав A и B;
II – двухкомпонентный расплав A и B и кристаллы А;
III, IV – двухкомпонентный расплав A и B и кристаллы химического соединения АхВy;
V – двухкомпонентный расплав A и B и кристаллы B;
VI – кристаллы A и кристаллы химического соединения АхВy;
VII – кристаллы химического соединения АхВy и кристаллы В
Рисунок 2. 30 – Диаграмма состояния А – B, компоненты которой
неограниченно растворимы в жидком состоянии и образуют между собой
в твердом состоянии химическое соединение, плавящееся конгруентно
Вертикаль, опущенная из точки D на ось состава, определяет состав химического соединения. Если A и B – металлы, то соединение АхВy называют интерметаллидом. Компоненты A и B сами могут быть химическими соединениями и, тем не менее, способными образовывать между собой в твердом агрегатном состоянии общее химической соединение, как, например, в системе CaCl2 – CsCl. Образующееся химическое соединение имеет формулу CaCl2. CsCl или в обобщенном виде CaCsCl3.
Анализ диаграмм с устойчивым химическим соединением удобнее проводить, если условно разделить диаграмму на две простых, например, диаграмма состояния компонента A (или B) и химического соединения (см. диаграммы с простой эвтектикой, раздел 2. 2. 3. 4).
|
|
|
