 |
2.1 Однокомпонентные системы
|
|
|
|
В зависимости от условий в однокомпонентной системе – индивидуальном веществе – могут сосуществовать одна, две или три устойчивые фазы. Например, при определенных условиях в воде могут находиться в равновесии жидкая вода и газообразная вода (водяной пар) или лед, жидкая вода и пары воды. В однокомпонентной системе, состояние которой определяется двумя параметрами – давлением и температурой – число фаз в равновесии не может быть больше 3. Покажем это с помощью правила фаз Гиббса при k = 1:
,
Откуда
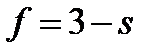
Максимальное число фаз получим при s = 0, следовательно, в однокомпонентной системе
Фазовые равновесия в однокомпонентной системе описываются уравнением Клаузиуса, которое в дифференциальной форме имеет вид
| (2. 6) |
Оно связывает производную давления насыщенного пара вещества по температуре 
с теплотой перехода одного моля вещества из одной фазы в другую Δ trsH (trs – сокращение от английского слова transition – переход, превращение) и изменением молярного объема при фазовом переходе Δ trsV при температуре фазового превращения. Насыщенным называется пар, находящийся в равновесии с жидкостью или твердой фазой.
Уравнение Клапейрона (2. 6) является универсальным уравнением, применимым к любому двухфазному равновесию. Рассмотрим применение уравнения Клапейрона к различным фазовым переходам, имеющим практическое значение.
Плавление – это переход вещества из твердого состояния в жидкое. В этом случае уравнение Клапейрона используют для анализа влияния давления на температуру плавления, поэтому его записывают в виде:
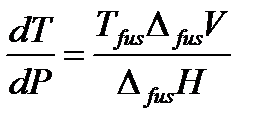
| (2. 7) |
где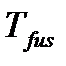 
– температура плавления вещества (fus – сокращение от английского слова fusion – плавление), 
– теплота плавления одного моля вещества, 
– изменение молярного объема вещества при фазовом переходе из твердого состояния в жидкое.
|
|
|
Характер изменения температуры плавления от давления определяется знаком производной 
. Так как T > 0 и Δ fusH > 0, то знак производной определяется знаком Δ fusV. Для большинства веществ объем при плавлении увеличивается Δ fusV > 0 и, следовательно, 
> 0. Поэтому для большинства веществ с ростом давления температура плавления увеличивается.
Однако, имеется небольшое число веществ (вода, висмут, галлий), для которых наблюдается иная (аномальная) зависимость температуры плавления от давления. У этих веществ при плавлении происходит уменьшение объема, а при кристаллизации – увеличение. Всем хорошо известно, что при замерзании воды ее объем увеличивается настолько, что в замкнутой системе происходит разрыв даже стальных и чугунных труб. Для этих веществ Δ fusV < 0 и, следовательно, 
< 0. Поэтому для воды, висмута, галлия с ростом давления температура плавления уменьшается
Испарение – это процесс перехода из жидкого состояния в газообразное. Газ, полученный испарением жидкости, называют паром. Изменение молярного объема при испарении представляет собой разность между объемом 1 моля вещества в газоообразном (Vg) и в жидком состоянии(Vl):
Δ vapV = Vg – Vl,
здесь vap – сокращение от английского слова vaporization – испарение.
В одинаковых условиях молярный объем любого вещества в газообразном состоянии во много раз больше, чем объем 1 моля в жидком виде. Например, объем 1 моля воды в газообразном состоянии при температуре кипения (373 К) и стандартном давлении (101, 320 кПа) составляет 30, 6 л, как легко рассчитать из уравнения Менделеева-Клапейрона (1. 1).
В жидком же состоянии при этих условиях 1 моль воды занимает объем 18, 8 см3. Поэтому можно считать, что
|
|
|
Δ vapV = Vg – Vl ≈ Vg
Выразив молярный объем газообразного вещества из уравнения Менделеева-Клапейрона (1. 1) и поставив его в уравнение Клапейрона, придем к уравнению Клапейрона-Клаузиуса:
| (2. 8) |
или в интегральной форме
| (2. 9) |
при условии, что теплота испарения не зависит от температуры.
Данное уравнение можно представить в виде
| (2. 10) |
где коэффициент A равен константе интегрирования (A = const), а 
.
Из уравнения 2. 10 видно, что график зависимости lnp = f(1/T) представляет собой прямую линию, из углового коэффициента которой можно найти теплоту испарения (рисунок 2. 1):
, а Δ vap H = B·R
| lnp |
| 1/T |
Рисунок 2. 1 – Зависимость логарифма давления насыщенного пара
от обратной температуры
Пример: Определим теплоту испарения этанола, если его температура кипения при давлении 13, 33 кПа составляет 34, 9°С, а при давлении 101, 38 кПа равна78, 4°С.
Решение: Температура кипения – это температура, при которой давление насыщенного пара вещества достигает внешнего давления. При этом испарение с поверхности жидкости уже невозможно, и газообразная фаза образуется внутри жидкости. Так возникают пузыри, характерные для кипения. Таким образом, при кипении давление насыщенного пара вещества равно внешнему давлению. Составим систему уравнений на основе уравнения Клапейрона-Клаузиуса для процесса испарения (2. 10):
Решив систему уравнений, получим
Теплоту испарения этанола найдем как
Δ vap H = BR= 5049·8, 314 = 41958, 44 Дж/моль = 41, 96 кДж/моль
Пример: Найдем, какое атмосферное давление на вершине горы, где вода кипит при 95°С. Теплота испарения воды по справочным данным составляет 40, 66 кДж/моль.
Решение: Известно, что при нормальном атмосферном давлении, равном 760 мм ртутного столба, температура кипения воды 100 °С. Из системы уравнений
находим
откуда p2 = 633 мм. рт. ст.
Если известна зависимость давления насыщенного пара вещества от температуры, то для более точного решения нужно найти коэффициенты А и В уравнения Клайперона-Клаузиуса методом наименьших квадратов. Зная численные значения этих коэффициентов, можно найти температуру кипения при любом давлении, также давление, при котором вещество закипит при определенной температуре, и молярную теплоту испарения.
|
|
|
Для процесса возгонки – перехода из твердого состояния в газообразное – интегральная форма уравнения Клапейрона-Клаузиуса имеет аналогичный вид:
| (2. 11) |
так как молярный объем любого вещества в твердом состоянии много меньше молярного объема вещества в газообразном состоянии и выполняется соотношение
Δ subV =Vg – Vs ≈ Vg.
Здесь Δ sub H – теплота возгонки, а Δ subV – изменение объема при возгонке 1 моля вещества (sub – сокращение от английского слова sublimation – сублимация, возгонка).
Зависимости давления насыщенного пара от температуры для различных фазовых превращений в равновесных условиях, вытекающие из уравнения Клапейрона-Клаузиуса, могут быть представлены в виде диаграммы состояния однокомпонентной системы.
На рисунке 2. 2 в качестве примера приведена диаграмма состояния воды.
Рисунок 2. 2 – Диаграмма состояния воды в области невысоких давлений
(приведена схематично без соблюдения масштаба)
На диаграмме видны:
- три области давлений и температур, при которых устойчиво существуют твердая (лед), жидкая и газообразная фазы;
- три линии, разделяющие эти области и отвечающие равновесному сосуществованию твердой и жидкой фаз (линия 1), твердой и газообразной фаз (3), жидкой и газообразной фаз(2);
- точка, в которой сходятся три линии, что соответствует равновесному сосуществованию трех фаз – твердой, жидкой и газообразной – так называемая, тройная точка.
Рассчитаем число степеней свободы в состоянии, которому соответствует тройная точка:
,
т. е. система нонвариантна. Это означает, что существуют только одно определенное значение температуры (0, 0099°С) и одно определенное значение давления насыщенного пара воды (610 Па), при которых сосуществуют три фазы. Изменение хотя бы одного из параметров – температуры или давления – приводит к изменению числа фаз в системе. Так как сосуществованию трех фаз соответствует строго определенная температура, тройную точку воды используют для создания эталона температуры. Первичный государственный эталон температуры хранится в Санкт-Петербурге во Всероссийском научно-исследовательском институте метрологии им. Д. И. Менделеева.
|
|
|
В любой точке, лежащей на линиях, соответствующих равновесию между двумя фазами, число степеней свободы равно:
Это означает, что, сохраняя двухфазное равновесие, независимо можно менять только один параметр – или давление, или температуру. Второй параметр будет изменяться в соответствии с уравнением Клапейрона-Клаузиуса.
|
|
|
