 |
2.2.3.7 Диаграмма плавкости, компоненты которой образуют между собой в твердом состоянии химическое соединение, плавящееся с разложением
|
|
|
|
2. 2. 3. 7 Диаграмма плавкости, компоненты которой образуют между собой в твердом состоянии химическое соединение, плавящееся с разложением
При образовании между компонентами A и B в твердом агрегатном состоянии химического соединения, плавящегося с разложением, на диаграммах на кривой ликвидуса отмечают наличие точки перитектики P. Эта температура примерно соответствует температуре плавления образующегося химического соединения АхВy. Составу соединения соответствует вертикальная линия постоянного состава (изоплета).
| I II P III IV V E VI |
| Tfus. B |
| Tfus. А |

Области:
I – двухкомпонентный расплав A и B;
II – двухкомпонентный расплав A и B и кристаллы А;
III – двухкомпонентный расплав A и B и кристаллы химического соединения АхВy;
IV – двухкомпонентный расплав A и B и кристаллы B;
V – кристаллы A и кристаллы химического соединения АхВy;
VI – кристаллы химического соединения АхВy и кристаллы В.
Рисунок 2. 31 – Диаграмма состояния А – B, компоненты которой
неограниченно растворимы в жидком состоянии и образуют между собой
в твердом состоянии химическое соединение, плавящееся инконгруентно
Все области диаграммы состояния (кроме области расплава I) являются гетерогенными, двухфазными. Для определения состава фаз в гетерогенной области условно следует провести ноду. Концы ноды показывают, какие из фаз находятся в равновесии друг с другом. Например, образующееся в твердом агрегатном состоянии химическое соединение находится в равновесии с кристаллами A – в области V, с расплавом – в области III, наконец, с кристаллами B – в области VI. В области II химическое соединение не существует, разлагается, вместо него в равновесии друг с другом находятся кристаллы A и расплав.
|
|
|
2. 2. 3. 8 Примеры анализа диаграмм состояния
Пример: Охарактеризуйте диаграмму плавкости системы Bi – Cd, приведенной на рисунке 2. 32.
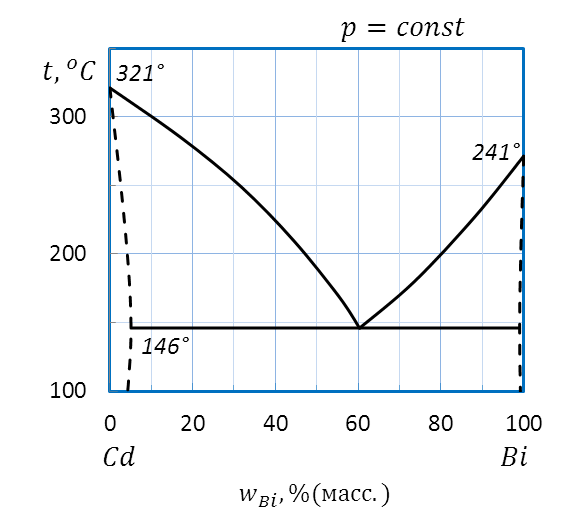
Рисунок 2. 32 – Диаграмма состояния Bi – Cd
Решение:
Диаграмма плавкости системы Bi – Cd относится к диаграммам состояния с неограниченной растворимостью в жидком и ограниченной растворимостью компонентов в твердом агрегатных состояниях.
Пример: Дайте описание состояния системы Bi – Cd (рисунок 2. 32) в различных условиях, расшифровав значение всех полей, линий и характерных точек диаграммы.
Решение:
По диаграмме плавкости Bi – Cd (рисунок 2. 32) определяем температуры плавления чистых веществ: 321˚ С для Cd и 241˚ С для Bi, соответственно.
Точка E на диаграмме (рисунок 2. 33) соответствует эвтектическому составу расплава. Прямая, проходящая через эту точку, называется линией эвтектики.
Кривая Tfus., Cd – E – Tfus., Bi – линия ликвидуса, показывает состав жидкой фазы.
Ломаная Tfus., Cd – E’E’’ –Tfus., Bi называется линией солидуса, позволяет определить состав твердой фазы.
Выше линии ликвидуса в области I система является гомогенной или однофазной, это область существования жидкой фазы (расплава).
Ниже линии ликвидуса система гетерогенная, т. е. двухфазная. В области II сосуществуют расплав и твердый раствор Bi в Cd, в области III – расплав и твердый раствор Cd в Bi, в гомогенной области IV – твердый раствор Bi в Cd, в гомогенной области V – твердый раствор Cd в Bi. Ниже линии эвтектики в гетерогенной области VI сосуществуют оба твердых раствора совместно Cd в Bi и Bi в Cd
|
|
|
На линии эвтектики E’EE” в равновесии находятся сразу три фазы: два твердых раствора составов E’ и E’’ и расплав состава Е.

Области: I – расплава, II - расплав и твердый раствор Bi в Cd,
III – расплав и твердый раcтвор Cd в Bi, IV – твердый раствор Bi в Cd,
V – твердый раствор Cd в Bi, VI – твердые растворы Cd в Bi и Bi в Cd
Линии: Tfus., Cd – E – Tfus., Bi – линия ликвидуса, Tfus., Cd – E’E’’ – Tfus., Bi – линия солидуса,
E’EE” –линия эвтектики
Рисунок 2. 33 – Диаграмма состояния Bi – Cd
Пример: Определите температуру начала кристаллизации расплава I (30 % (масс. ) Bi, 300˚ С) системы Bi – Cd (рис. 2. 32) и состав первых кристаллов. Как изменяется состав расплава и твердой фазы при охлаждении?
Решение:
Опускаем перпендикуляр от точки I на ось состава (рис. 2. 34). Прямая пересекает линию ликвидуса Tfus., Cd – E – Tfus., Bi при температуре 250˚ С в точке a – температуре начала кристаллизации.

Рисунок 2. 34 – Диаграмма состояния Bi – Cd.
Определение температуры начала кристаллизации расплава I
и состава первых кристаллов
Для определения состава первых кристаллов проводим при постоянной температуре внутри гетерогенной области ноду (линию, соединяющую фазы, находящиеся в равновесии) от линии пересечения кривой ликвидуса до линии солидуса Tfus., Cd – E’E’’ – Tfus., Bi– точка b. Первые кристаллы – твердый раствор Bi в Cd состава примерно 2 масс. % Bi и 98 масс. % Cd.
При дальнейшем охлаждении (рисунок 2. 35) от точки а до точки а’ в системе сосуществуют две фазы: расплав и твердый раствор Bi в Cd. Состав твердого раствора при понижении температуры меняется по кривой Tfus., Cd– E’ от b (2 % (масс. ) Bi) до точки E’ (5 % (масс. ) Bi), поскольку при какой бы температуре внутри этой области не проводили бы ноду, один конец ее упирается в линию солидуса Tfus., Cd– E’, ограничивающей область существования твердого раствора. Другой конец ноды оказывается на линии ликвидуса Tfus., Cd– E. Состав жидкой фазы при понижении температуры от точки a до точки a’ меняется от точки a (30 % (масс. ) Bi) до точки E (60 % (масс. ) Bi) по кривой ликвидуса.

Рисунок 2. 35 – Диаграмма состояния Bi – Cd.
Определение состава фаз при охлаждении расплава I
Таким образом, при кристаллизации жидкости исходного состава I меняется как состав твердой, так и жидкой фаз. В обеих фазах при понижении температуры увеличивается содержание Bi, количество твердого раствора увеличивается, количество расплава уменьшается.
|
|
|
По достижении линии эвтектики E’EE” из последних капелек расплава состава Е помимо твердого раствора состава E’ начинает кристаллизоваться еще один твердый раствор состава E” (примерно 98% (масс. ) Bi). Температура системы остается постоянной, пока кристаллизация полностью не закончится.
Последующее понижение температуры свидетельствует об охлаждении гетерогенной системы, состоящей из смеси твердых растворов (рисунок 2. 35: стрелки на диаграмме от точек E’ и E” вниз).
Пример: Определите температуру начала плавления, количество и состав фаз при этой температуре системы состава II (80 %(масс. ) Bi, 100˚ С) диаграммы плавкости Bi – Cd, приведенной на рисунке 2. 32.
Решение:
Проводим перпендикуляр от точки II вверх (рисунок 2. 36). Штриховая прямая пересекает линию эвтектики E’ – E – E’’ при температуре 145˚ С – температуре начала плавления.
При температуре эвтектики система состоит из трех фаз: точка E’ показывает состав одной твердой фазы – твердый раствор Bi в Cd (~ 5 % (масс. ) Bi), точка E’’ – состав другой твердой фазы – твердый раствор Cd в Bi (~ 98 % (масс. ) Bi), наконец, точка E соответствует составу первых капель жидкой фазы – эвтектического расплава. Состав расплава – 60 % (масс. ) Bi и 40 % (масс. ) Cd.

Рисунок 2. 36 – Диаграмма состояния Bi – Cd.
Определение температуры начала плавления
Пример: Начертите схематические кривые охлаждения расплавов составов I (30 % (масс. ) Bi), II (80 % (масс. ) Bi) и III (100 % (масс. ) Bi) диаграммы плавкости Bi – Cd (рисунок 2. 32), определив число и состав фаз и рассчитав число степеней свободы в характерных точках и на каждом участке кривых охлаждения.
Решение:
Проводим перпендикуляр (или изоплету, т. е. линию постоянного состава, проходящую через несколько температур) от точки I (30 % (масс. ) Bi) при температуре 300˚ С вниз до оси состава. Штриховая прямая пересекает линию ликвидуса в точке а и линию эвтектики в точке a’, на оси состава ставим точку а”.
|
|
|
Рассчитываем число степеней свободы системы s по правилу фаз Гиббса для диаграммы состояния, построенной при постоянном давлении. Для расчета выделяем интервалы Ia, aa’, точку a’ и интервал a’a’’. Во всех случаях система является двухкомпонентной: Cd и Bi, т. е. k = 2.
Ia:  (f = 1, одна жидкая фаза – двухкомпонентный расплав).
(f = 1, одна жидкая фаза – двухкомпонентный расплав).
aa’:  (f = 2, сосуществуют две фазы – расплав и твердый раствор Bi в Cd).
(f = 2, сосуществуют две фазы – расплав и твердый раствор Bi в Cd).
a’: 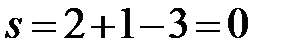 (f = 3, в равновесии три фазы – расплав, твердый раствор Bi в Cd и твердый раствор Cd в Bi).
(f = 3, в равновесии три фазы – расплав, твердый раствор Bi в Cd и твердый раствор Cd в Bi).
a’a’’: 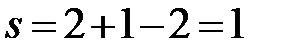 (f = 2, сосуществуют две фазы – твердый раствор Bi в Cd и твердый раствор Cd в Bi).
(f = 2, сосуществуют две фазы – твердый раствор Bi в Cd и твердый раствор Cd в Bi).

Рисунок 2. 37 – Диаграмма состояния Bi – Cd.
Построение кривой охлаждения расплава I
Переносим точки изменения числа фаз a и a’ на соседний график температура - время.
Чертим кривую охлаждения, учитывая, что падение температуры при охлаждении системы более резкое, если система бивариантна (s = 2); более пологое вследствие выделения теплоты при кристаллизации, если система моновариантна(s = 1). Наконец, температура остается постоянной для нонвариантной системы (s = 0).
В случае II (рисунок 2. 38) также проводим изоплету (или перпендикуляр) от температуры 300˚ С вниз до оси состава. Штриховая прямая пересекает линию ликвидуса в точке b и линию эвтектики в точке b’, на оси состава ставим точку b”.

Рисунок 2. 38 – Диаграмма состояния Bi – Cd.
Построение кривой охлаждения расплава II
Для расчета выделяем интервалы IIb, bb’, точку b’ и интервал b’b’’. Во всех случаях система так же, как и в первом случае, является двухкомпонентной: Cd и Bi, т. е. k = 2.
IIb:  (f = 1, одна жидкая фаза – двухкомпонентный расплав).
(f = 1, одна жидкая фаза – двухкомпонентный расплав).
bb’:  (f = 2, сосуществуют две фазы – расплав и твердый раствор Cd в Bi).
(f = 2, сосуществуют две фазы – расплав и твердый раствор Cd в Bi).
b’:  (f = 3, в равновесии три фазы – расплав, твердый раствор Cd в Bi и твердый раствор Bi в Cd).
(f = 3, в равновесии три фазы – расплав, твердый раствор Cd в Bi и твердый раствор Bi в Cd).
b’b’’: 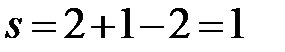 (f = 2, сосуществуют две фазы – твердый раствор Cd в Bi и твердый раствор Bi в Cd).
(f = 2, сосуществуют две фазы – твердый раствор Cd в Bi и твердый раствор Bi в Cd).
Сносим точки изменения числа фаз b и b’ на график температура-время.
Рисуем схематично кривую охлаждения аналогично примеру I.
В случае III (рисунок 2. 39) проводим изоплету от температуры 300˚ С до оси состава. Штриховая прямая пересекает температуру плавления Bi в точке c, на оси состава ставим точку c’.
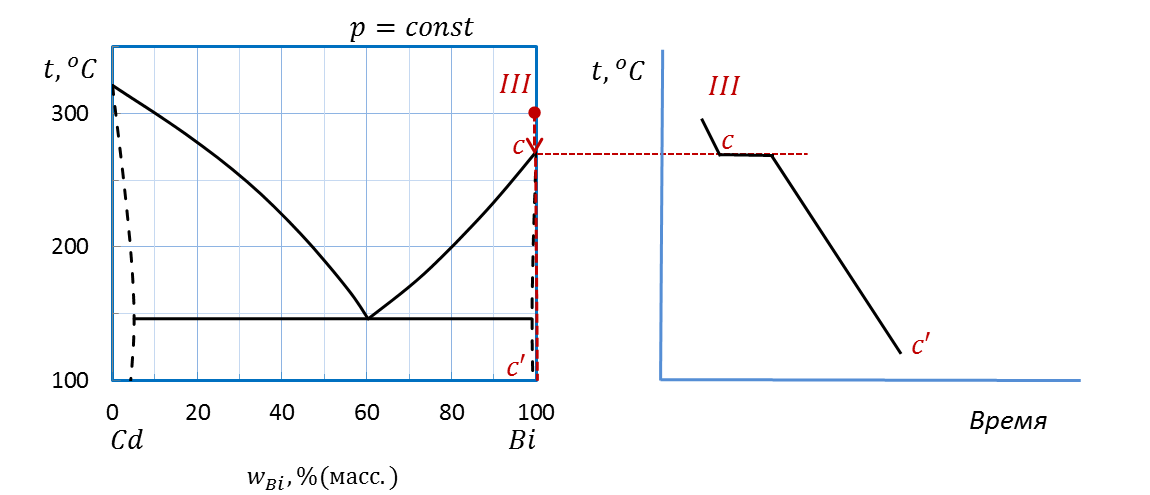
Рисунок 2. 39 – Диаграмма состояния Bi – Cd.
Построение кривой охлаждения расплава III
Для расчета выделяем интервалы IIIc, точку c и интервал cc’. Во всех случаях система является однокомпонентной: один компонент Bi, т. е. k = 1.
IIIc:  (f = 1, одна жидкая фаза – жидкий Bi).
(f = 1, одна жидкая фаза – жидкий Bi).
c:  (f = 2, в равновесии две фазы – жидкий и кристаллический Bi).
(f = 2, в равновесии две фазы – жидкий и кристаллический Bi).
|
|
|
cc’:  (f = 1, одна твердая фаза – кристаллы Bi).
(f = 1, одна твердая фаза – кристаллы Bi).
Переносим точку изменения числа фаз c на график температура – время.
Чертим кривую охлаждения аналогично случаям I и II.
Пример: Начертите схематическую кривую охлаждения расплава состава a (60 % B) диаграммы плавкости A – B (рисунок 2. 26), определив число и состав фаз и рассчитав число степеней свободы в характерных точках и на каждом участке кривой охлаждения.
Решение:
Проводим изоплету (рисунок 2. 40) от фигуративной точки d до оси состава. Штриховая прямая пересекает кривую ликвидуса в точке d’, кривую солидуса – в точке d’’, на оси состава ставим точку d’’’.
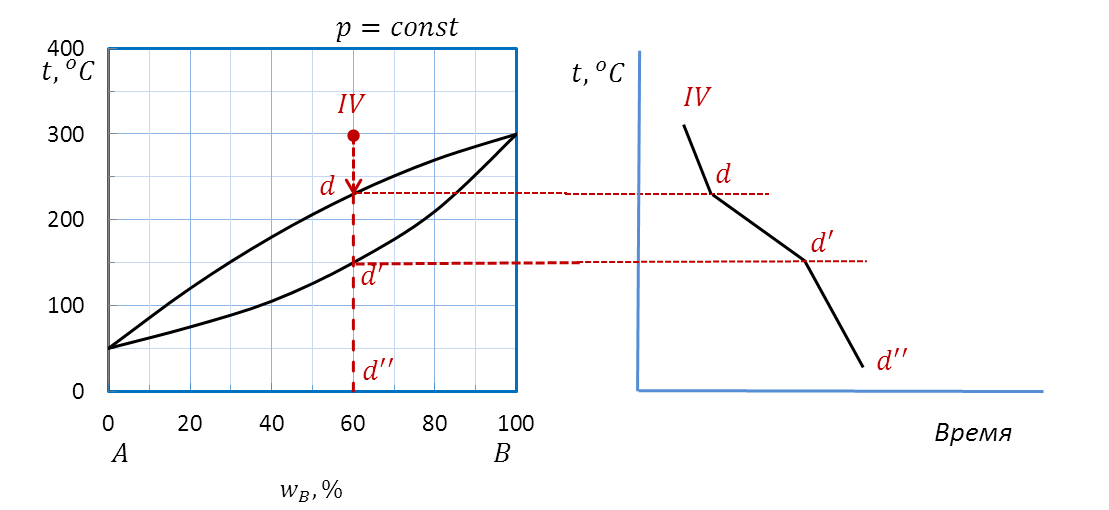
Рисунок 2. 40 – Диаграмма состояния A – B.
Построение кривой охлаждения расплава IV.
Для расчета вариантности системы выделяем интервалы dd’, d’d’’ и интервал d’’d’’’. Во всех случаях система является двухкомпонентной, т. е. k = 2.
dd’:  (f = 1, одна жидкая фаза – расплав).
(f = 1, одна жидкая фаза – расплав).
d’d’’:  (f = 2, в равновесии две фазы – расплав и твердый раствор A и B).
(f = 2, в равновесии две фазы – расплав и твердый раствор A и B).
d’’d’’’:  (f = 1, одна твердая фаза – твердый раствор A и B).
(f = 1, одна твердая фаза – твердый раствор A и B).
Переносим точки изменения числа фаз на график температура – время.
Чертим кривую охлаждения. На кривой охлаждения видны точки перегиба, соответствующие температурам начала (d’) и конца кристаллизации (d’’).
Пример: Вычислите массы равновесных фаз при температуре 200оС для 10 кг исходной смеси состава l (20 %(масс. )Bi) диаграммы плавкости Cd – Bi, приведенной на рисунке 2. 32.
Решение:
Для вычисления масс фаз, находящихся в равновесии, при температуре 200оС проводим через состав l (20 %(масс. ) Bi) ноду внутри гетерогенной области kn. Один конец ноды k показывает состав твердой фазы – примерно 4 % (масс. ) Bi и 96 %(масс. ) Cd, другой конец ноды n находится на кривой ликвидуса и позволяет определить состав сосуществующей жидкой фазы: 47 % (масс. ) Bi и 53 % (масс. ) Cd, соответственно.
Составляем правило рычага:
kl ∙ ms = ml ∙ ln.
При подстановке вместо отрезков разности составов, выраженных, например, по %(масс. ) Bi, получаем уравнение:
 j
j
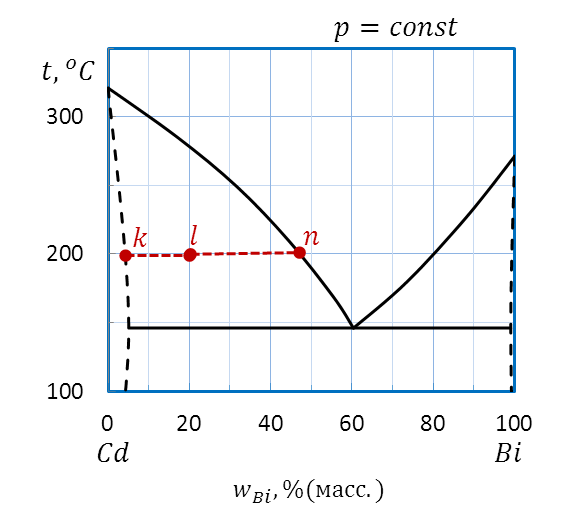
Рисунок 2. 41 – Диаграмма состояния Bi – Cd.
Вычисление массы равновесных фаз системы состава l по правилу рычага
Второе уравнение, необходимое для решения, связывает массы равновесных фаз и массу исходной смеси (10 кг):
 кг
кг
Решаем совместно оба уравнения. Результат:
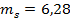 кг;
кг;
 кг.
кг.
Пример: Определите формулу химического соединения, образующегося между компонентами системы Te – Al (рисунок 2. 42) в твердом агрегатном состоянии.
Решение:
В системе Te – Al между компонентами в твердом агрегатном состоянии возможно образование химического соединения AlxTey с температурой плавления 895оС.
Для определения х и y в формуле этого соединения пересчитываем состав по первому и второму компонентам, выраженный в %(масс. ) (w), в % (ат. ) или %(мол. ) (x) по формулам:
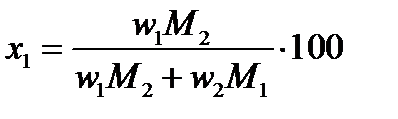 и и 
| (2. 30) |
Для данной диаграммы wAl = 12%(масс. ), wTe = 88%(масс. ), MAl = 26, 98 г/моль, MTe = 127, 60 г/моль.

Рисунок 2. 42 – Диаграмма состояния Te – Al.
Подстановка значений дает:
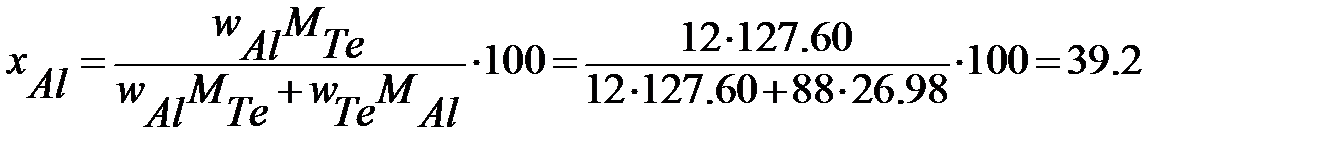 % (мол. ) Al,
% (мол. ) Al,
 % (мол. ) Te.
% (мол. ) Te.
Отношение полученных составов, выраженных в % (ат. ) или % (мол. ), позволяет определить формулу химического соединения AlxTey:
 или Al2Te3.
или Al2Te3.
|
|
|


