2.1.1 Многовариантное задание №3 «Анализ фазового равновесия жидкость – пар в однокомпонентной системе»

2. 1. 1 Многовариантное задание №3 «Анализ фазового равновесия жидкость – пар в однокомпонентной системе»

 

1. Для вещества А, заданного в таблице 2. 1, используя данные справочника [2] по зависимости температуры кипения веществ от давления, постройте кривую испарения в координатах p = f (T)и lnp = f(1/Т).

2. Определите коэффициенты уравнения lnp = .

3. Вычислите теплоту испарения Δ _vapН для вещества А (кДж /моль), используя коэффициент В, найденный в п. 2.

4. Вычислите температуру кипения при р = 1, 0132·10⁵ Па. Сопоставьте ее с табличным значением.

5. Вычислите давление насыщенного пара при температуре t _x, указанной в задании (таблица 2. 1).

Таблица 2. 1 – Варианты заданий

Вариант	Вещество А		Температура, t x , º С
			Подвариант
	C2HCl3O2	трихлоруксусная кислота
	C2H2Cl2O2	дихлоруксусная кислота
	C2H3ClO2	хлоруксусная кислота
	C2H3N	ацетонитрил
	C2H4O2	уксусная кислота
	C2H4Cl2	1, 2-дихлорэтан
	C2H6O	этанол
	C2H6O2	этиленгликоль
	C3H6O	ацетон	-1, 5
	C3H6O2	метилацетат
	C3H6O2	пропионовая кислота
	C3H8O	пропанол
	C4H8O2	масляная кислота
	C4H8O2	1, 4-диоксан
	C4H8O2	этилацетат
	C4H10O	диэтиловый эфир		-20	-10
	C4H10O	бутанол
	C5H5N	пиридин
	C5H12O	амиловый спирт
	C6H5Br	бромбензол
	C6H5Cl	хлорбензол
	C6H5I	иодбензол
	C6H5NO3	нитробензол
	C6H6	бензол
	C7H8	толуол
	C7H16	гептан

2. 2 Двухкомпонентные системы

2. 2. 1 Идеальные и неидеальные растворы

 

Растворомназывают гомогенную систему переменного состава, состоящую как минимум из двух компонентов. Различают газообразные, жидкие и твердые растворы. Растворы бывают с неограниченной и ограниченной растворимостью компонентов друг в друге.

При описании жидких растворов различают растворитель и растворенное вещество. Растворителем считают то вещество, которое в чистом виде находится в том же агрегатном состоянии, что и раствор. Если в чистом виде компоненты и раствор находятся в одинаковом агрегатном состоянии, то растворителем считают то вещество, которого больше. Обычно свойства растворителя обозначают подстрочным индексом «1», а растворенного вещества - индексом «2».

По характеру взаимодействия компонентов раствора различают идеальные и неидеальные растворы.

В идеальных растворах, состоящих из двух неограниченно растворимых друг в друге компонентов А и В, энергия взаимодействия двух различных частиц (Е_А-В) такая же, как и двух одинаковых (Е_А-А и Е_В-В):

 

                                                        Е_А-В = (Е_А-А + Е_В-В).                                              (2. 12)

 

Образование идеальных растворов происходит атермически (без теплового эффекта, теплота смешения Δ _mixH= 0) и без изменения объема (Δ _mixV= 0). Изменение энтропии при образовании идеальных растворов такое же, как при смешении идеальных газов:                  

 

                                              Δ _mixS= - R(x_Аlnx_А + x_Вlnx_В).                                              (2. 13)

 

 

Идеальные жидкие растворы описываются законом Рауля:

 

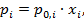                                                                                             (2. 14)

 

где  - парциальное давление насыщенного пара i-го компонента над раствором;

      - давление насыщенного пара над чистым жидким i-м компонентом;

      – молярная доля i-го компонента в растворе.

Для идеальных растворов закон Рауля выполняется для всех компонентов при всех температурах и концентрациях.

Химический потенциал компонента идеального раствора:

 

                                                                                       (2. 15)

 

Идеальные растворы образуются из веществ, очень близких по своим свойствам (изотопы, оптические изомеры, гомологи).

В большинстве случаев при смешении жидких компонентов образуются неидеальные растворы. Большинство реальных растворов являются неидеальными. В таких растворах энергия взаимодействия разнородных частиц отличается от энергии взаимодействия одинаковых частиц:

 

                                            Е_А-В (Е_А-А + Е_В-В).                                                (2. 16)

 

Образование неидеальных растворов сопровождается тепловым эффектом(Δ _mixH  0) и/или изменением объема (Δ _mixV  0). Изменение энтропии при смешении компонентов неидеальных растворов отличается от энтропии смешения идеальных газов (2. 13).

Для неидеальных растворов уравнение Рауля неприменимо ( ). (Оно может быть применимо только по отношению к растворителю в очень разбавленных реальных растворах).

Различают неидеальные растворы с положительными и отрицательными отклонениями от идеальности (от закона Рауля). При положительных отклонениях  от идеальности энергия взаимодействия разнородных частиц в растворе меньше энергии взаимодействия одинаковых частиц:

 

                                                Е_А-В (Е_А-А + Е_В-В).                                            (2. 17)

 

Такие растворы образуются, как правило, с поглощением тепла (Δ _mixH  0) и с увеличением объема (Δ _mixV  0).

Для систем с положительными отклонениями от закона Рауля общее давление насыщенного пара над неидеальным раствором больше, чем над идеальным раствором p p^ид. Силы межчастичного взаимодействия между молекулами в растворе меньше, чем между молекулами чистых компонентов, и, следовательно, перевод компонентов такого раствора в пар требует меньших затрат энергий, чем перевод в пар компонентов идеального раствора.

При отрицательных отклонениях от закона Рауля энергия взаимодействия разнородных частиц в растворе больше энергии взаимодействия одинаковых частиц:

 

                                                Е_А-В (Е_А-А + Е_В-В),.                                         (2. 18)

 

Образование такого раствора сопровождается выделением тепла (Δ _mixH  0) и уменьшением объема (Δ _mixV  0).

Для систем с отрицательными отклонениями от закона Рауля общее давление насыщенного пара над неидеальным раствором меньше, чем над идеальным раствором p 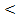p^ид. Силы межчастичного взаимодействия между молекулами в растворе больше, чем между молекулами чистых компонентов, и, следовательно, перевод компонентов такого раствора в пар требует больших затрат энергий, чем перевод в пар компонентов идеального раствора.

Для описания свойств неидеальных растворов вводят понятие активности i-го компонента в растворе .

Активность компонента в растворе  – это величина, прямо пропорциональная концентрации, которая используется вместо концентрации в уравнениях, выведенных для идеальных растворов, так чтобы эти уравнения выполнялись и для неидеальных растворов. Т. е.

 

,                                                  (2. 19)

 

где 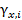 - коэффициент активности.

Коэффициент активности  характеризует отклонение свойств компонента неидеального раствора от свойств компонента идеального раствора. Коэффициент активности зависит от концентрации компонента в растворе.

Значение и обозначение коэффициента активности зависит от того, в каких единицах выражается концентрация компонента. Если концентрация выражена в мольных долях, то коэффициент активности обозначается 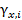. Для молярной концентрации соответствующий коэффициент активности обозначается 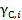. Для моляльной концентрации коэффициент активности обозначается  или .

Химический потенциал компонента неидеального раствора выражается уравнением:

 

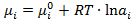                                                                                        (2. 20)

 

Для неидеального раствора используется уравнение, аналогичное закону Рауля:

 

                                                                                                                   (2. 21)

 

где  – давление насыщенного пара i-го компонента над неидеальным раствором (экспериментально определенное давление).

Пример: Вычислим по закону Рауля давление водяного пара над водным раствором C₁₂H₂₂O₁₁ (m =1, 101 моль/кг Н₂О) при 75˚ С. Давление насыщенного водяного пара над чистой водой при 75˚ С p_{0, 1} = 38, 548 кПа. Рассчитаем активность и коэффициент активности воды, если экспериментально измеренное давление водяного пара над раствором p =37, 954 кПа.

Решение:

Мольная доля воды  в растворе определяется как:

 

 

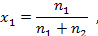
где  – количества молей растворителя и растворенного вещества, соответственно.

Поскольку моляльность раствора - это количество молей растворенного вещества в 1000 граммах растворителя, запишем 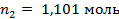. Количество молей воды, находящихся в 1000 г, рассчитаем:

 

 

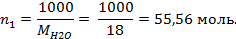
Отсюда

 

Давление водяного пара над водным раствором C₁₂H₂₂O₁₁ рассчитаем по закону Рауля (2. 14):

 

.

 

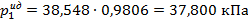Можно видеть, что  Следовательно, наблюдается положительное отклонение от закона Рауля.

Рассчитаем активность воды из уравнения (2. 21):

 

 37, 954/38, 548 = 0, 9846

 

Найдем коэффициент активности воды по уравнению (2. 19):

 

 

Для разбавленного водного раствора C₁₂H₂₂O₁₁ наблюдаются незначительные положительные отклонения от идеальности.

 

Жидкие растворы обладают некоторыми свойствами, не зависящими от природы растворенного вещества, а определяющимися только числом частиц растворенного вещества в растворе. Такие свойства называются коллигативными. К таким свойствам относятся понижение температуры замерзания (или плавления) и повышение температуры кипения раствора по сравнению с чистым растворителем и осмотическое давление. Для идеальных растворов справедливы уравнения:

 

                                                ,                                                   (2. 22)

                                                  ,                                                 (2. 23)

 

                                                       ,                                                      (2. 24)

 

где – понижение температуры замерзания (плавления) раствора по сравнению с температурой замерзания (плавления) растворителя;

 – криоскопическая постоянная, зависящая только от свойств растворителя;

 – моляльность раствора, моль/кг растворителя;

 – повышение температуры кипения раствора по сравнению с температурой кипения растворителя;

 – эбулиоскопическая постоянная, зависящая только от свойств растворителя;

 – осмотическое давление, Па;

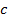 – молярная концентрация, моль/м³.

 

При диссоциации или ассоциации растворенного вещества число частиц в растворе изменяется. Это изменение можно учесть, введя в уравнения изотонический коэффициент Вант-Гоффа i. Тогда уравнения (2. 22) – (2. 24) запишутся в виде

 

 

,                                                         (2. 25)

 

 ,                                                    (2. 26)

 ,                                                     (2. 27)

                                                

Изотонический коэффициент  Вант-Гоффа показывает, во сколько раз изменяется число частиц в растворе вследствие диссоциации или ассоциации молекул. В разбавленных растворах сильных электролитов величина этого коэффициента приближается к небольшим целочисленным значениям. Так, осмотическое давление (p) разбавленного раствора хлорида натрия с концентрацией с равно 2RTc (т. е. i =2). Это легко объяснялось тем, что концентрация частиц в растворе вдвое превышает величину концентрации, которая была рассчитана исходя из навески соли NaCl, растворенной в определенном объеме. Небольшие отклонения от целочисленных значений связывали с экспериментальными ошибками. Теперь в этом усматривают влияние коэффициентов активности.

Для слабых электролитов получили дробные значения i, зависящие от общей концентрации электролита. Используя теорию электролитической диссоциации Аррениуса можно установить связь между изотоническим коэффициентом Вант-Гоффа и степенью диссоциации a:

 

                                              .                                                    (2. 28) 

 

Определяя экспериментально осмотическое давление или понижение температуры замерзания раствора, можно вычислить коэффициент Вант-Гоффа i, а затем определить степень диссоциации a и рассчитать практическую константу диссоциации К_с для слабого электролита. Величину К_с также можно определить, используя кондуктометрический и потенциометрический методы. Рассчитанные разными методами К_с хорошо согласуются друг с другом, что служит убедительным доказательством справедливости электролитической теории Аррениуса для слабых электролитов.

Для сильных электролитов в разбавленных растворах степень диссоциации a 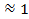, т. е. число частиц должно увеличиться в nраз. Однако в действительности коэффициент Вант-Гоффа всегда меньше n, так как ионы в растворе связаны силами электростатического взаимодействия и не могут проявлять себя как вполне свободные частицы. Чем больше силы межионного взаимодействия, тем больше отклоняется данный реальный раствор от идеального раствора и тем меньше i.

 

Пример: Определим, подчиняется ли идеальным законам раствор CaCl₂ − H₂O следующего состава: 0, 944 г CaCl₂, 150 г H₂O. Экспериментально определенное понижение температуры замерзания  = 0, 272 градуса.

Решение:

Рассчитаем моляльность раствора:

 

 

Найдем понижение температуры замерзания раствора, считая раствор идеальным, воспользовавшись справочными данными о криоскопической постоянной воды [2]:

 

.

 

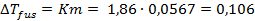Сравнение рассчитанной величины с экспериментальным значением  показывает, что данный раствор не является идеальным. В результате диссоциации молекул CaCl₂ число частиц увеличивается.

 

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: