Численные методы минимизации функции

 

Численное решение задачи минимизации (1), как правило, связано с построением минимизирующей последовательности точек x⁰, x¹, x²,…, xⁿ,…, обладающих свойством

f (x^k) < f (x^k-1), k =0,1,… (3)

 

Общее правило построения минимизирующей последовательности имеет вид

x ^k+1= x ^k+ t _k d ^k, k =0,1,…,

 

где х⁰ - начальная точка поиска; d^k - приемлемое направление перехода из точки x^k в точку x^k+1, которое обеспечивает выполнение условий (3) и называется направлением спуска; t_k - величина шага. Начальная точка поиска задается исходя из физического содержания решаемой задачи и априорных данных о существовании и положении точек экстремума.

При решении вопроса о выборе численного метода рекомендуется оценить поведение линий уровня целевой функции в окрестностях предполагаемой точки экстремума. Число m = L/l, где L и l - максимальное и минимальное собственные значения гессиана функции f в предполагаемой точке экстремума x⁰ ( характеризующее разброс собственных значений оператора f (x)), называется числом обусловленности гессиана функции f в точке x⁰. Если m >> 1, то функция f называется плохо обусловленн ой или овражн ой. Овражность, то есть вытянутость линий уровня вдоль одного направления, приводит к тому, что градиентные методы поиска экстремума функции сходятся медленно.

В зависимости от наивысшего порядка частных производных функции f (x), используемых для формирования d^k и t_k, численные методы принято делить на три группы:

Методы нулевого порядка, использующие информацию только о значениях функции f (x) ( методы деформируемого многогранника, конфигураций). Эти методы могут применяться в тех случаях, когда функция задана неявно или не задана аналитически, но известен ряд значений функции или эти значения вычисляются непосредственно в ходе реализации алгоритма. Они также могут быть полезны в случаях, когда производные функции могут быть заданы аналитически, но их выражения очень громоздки.

Методы первого порядка, использующие информацию о значениях самой функции f (x) и ее первых производных (методы наискорейшего градиентного спуска, дробления шага, Гаусса-Зейделя, Флетчера-Ривса).

Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) ( метод Ньютона и его модификации).

Метод конфигураций (Хука - Дживса)

Следует выделить два этапа метода конфигураций:

1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам.

Исследующий поиск начинается в точке х⁰, называемой старым базисом. Направления поиска - координатные направления. По каждому направлению поочередно с шагом + t₀ (- t₀) проверяется выполнение условия (2) и в качестве нового базиса берется точка с координатами, полученными в результате удачных шагов из начальной точки по каждому направлению.

Направление от старого базиса к новому задает направление ускорения поиска: в качестве следующей точки минимизирующей последовательности проверяется точка y¹= x⁰+ l (x¹- x⁰). Здесь l - ускоряющий множитель, задаваемый пользователем. Если полученная точка является удачной, то она берется в качестве следующей точки для исследования. В противном случае исследование ведется из точки x¹.

Метод деформируемого многогранника (Нелдера - Мида).

При решении задачи поиска минимума функции f (x) методом Нелдера-Мида строится последовательность множеств из n +1 точек, которые являются вершинами выпуклого многогранника. На каждом последующем k +1-м шаге из системы точек xⁱ (k), i =1, …, n +1, полученной на k- м шаге, выводится точка x^h (k), в которой функция f (x) имеет наибольшее значение (худшая точка). Вместо x^h (k) в систему вводится новая точка, выбираемая на отрезке прямой, проходящей через худшую точку и центр тяжести оставшихся n вершин многогранника:

x^{n +2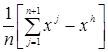}=  - центр тяжести;

x^{n +3}= x^{n +2}+a (x^{n +2} - x^h)

 

новая точка (“растянутое” отражение наихудшей вершины).

Метод дробления шага.

В данном методе строится релаксационная последовательность точек, т.е. таких точек { x^k }, k= 0,1,…, что f (x^k) < f (x^k-1), k =0,1,…. Точки последовательности { x^k } вычисляются по следующему правилу:

x^k+1= x^k- t_kgrad f (x^k), k =0,1,… (4)

Начальная точка х⁰ и начальный шаг t₀ задаются пользователем. Величина шага t₀ не изменяется до тех пор, пока функция убывает в точках последовательности. Это контролируется путем проверки выполнения условия f (x^k+1) - f (x^k) <0 (или <-ε). Если условие убывания не выполняется, то величина шага уменьшается, как правило, вдвое, т.е. t_k= t_k /2.

Метод наискорейшего градиентного спуска

Как и в предыдущем методе, точки релаксационной последовательности { x^k }, k= 0,1,… вычисляются по правилу (4). Точка х⁰ задается пользователем; величина шага t_k определяется из условия минимума одномерной функции φ (t_k) = f (x^k- t_k grad f (x^k)). Задача минимизации функции φ (t_k) может быть решена с использованием необходимого условия минимума 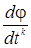=0 с последующей проверкой достаточного условия минимума 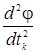>0 или с использованием численных методов.

Метод сопряженных направлений (Флетчера - Ривса).

В данном методе используются свойства векторов, сопряженных относительно некоторой матрицы.

Определение. Векторы p и q называются сопряженными относительно матрицы Q, если выполняется равенство pQq =0.

Точки релаксационной последовательности { x^k }, k =0,1,… вычисляются по правилу

x^{k+ 1} = x^k- t_kd^k, k =0,1,…;

d^k = - grad f (x^k) + β _{k- 1} d^{k - 1}; (5)

d⁰= - grad f (x⁰);

β _k-1=║ grad f (x^k) ║ ²∕ ║ grad f (x^{k- 1} ) ║ ².

 

Точка х⁰ задается пользователем; величина шага t_k определяется из условия минимума функции φ (t) = f (x^k- td^k). Задача минимизации одномерной функции φ (t_k) может быть решена с использованием необходимого условия минимума 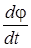=0 с последующей проверкой достаточного условия минимума 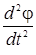>0 или с использованием численных методов. Коэффициент β _{k- 1} вычисляется из условия сопряженности направлений d^k и d^{k- 1}.

Метод Ньютона.

Строится последовательность точек { x^k }, k =0,1,…, таких, что , k =0,1,… Точки последовательности { x^k } вычисляются по правилу x^k+1= x^k+ d^k, k =0,1,… Точка х⁰ задается пользователем с учетом знакопостоянства и невырожденности матрицы Гессе в задаваемой начальной точке и близости выбранной точки к предполагаемой точке минимума. Направление спуска определяется для каждого значения k по формуле d^k =- H^-1 (x^k) grad f (x^k), где Н - матрица Гессе.

12345

Поделиться:

Воспользуйтесь поиском по сайту: