 |
Пример выполнения лабораторной работы
|
|
|
|
Минимизировать нелинейную функцию 
при условиях 
и 
, применяя метод функции Лагранжа. Проверить справедливость оценки изменения целевой функции (9).
Допустимая область - часть сферы 
, лежащая в подпространстве
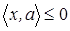, a = (1, 1,1).
Рассмотрим случай 
. Если при этом 
, то 
.
Из (21) - (23) ® 
, что противоречит (28).
Если 
, то 
(иначе получаем противоречия в (21) - (23)).
Из (21) - (23) ® 
. Подставим в (26): 
. Отсюда 
, что противоречит исходному предположению 
.
Рассмотрим теперь случай 
.
Если 
, то получаем точку 
(из (1′) … (3′), (7′)).
Остальные "симметричные" точки здесь и далее приводить не будем.
Если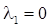 
, 
, 
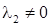, то
,
,
.
Далее получаем точки
и 
. 
, 
.
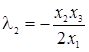Для 
значение
, для 
значение 
.
Если 
, 
, то
Если 
, то
и 
.
Следовательно, 
и 
. Однако, 
, значит, пришли к
противоречию.
Таким образом, 
.
Суммирование первых трех уравнений дает уравнение
,
в котором последнее слагаемое равно нулю, поэтому
.
С другой стороны,
и 
.
Следовательно, 
,
откуда 
. Если 
, то 
.
Разделим равенства на 
: 
. Однако, если 
, то их произведение не может быть равно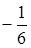 
. Значит, 
. Если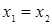 
, получаем следующую систему:
.
Получаем точку
(в силу симметрии переменных х 1, х 2, х 3 координаты можно переставить),
, 
.
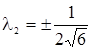Предположив 
, получим те же результаты.
Найдены следующие точки:
, 
, 
;
, , 
, 
;
, 
, 
, ;
, 
, , 
.
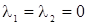Запишем второй дифференциал обобщенной функции Лагранжа.
, 
, 
;
.
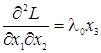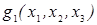
является активным ограничением только для точки 
.
Применим достаточное условие минимума второго порядка к этой точке:
Подставив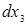 
и 
во второй дифференциал функции Лагранжа, получим
|
|
|
.
Запишем матрицу квадратичной формы относительно приращений:
.
Для "верхнего" знака 
матрица
.
Для "нижнего" знака элементы матрицы меняют знак. Согласно критерию Сильвестра, в этой точке нет экстремума.
Сравним значения функции в остальных точках:
; 
; 
.
Точкой глобального минимума является
,
значение функции в этой точке
-0, 192450. 
.
Проверим справедливость оценки 
для точки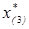 
, 
.
Возьмем вектор 
, ему соответствуют множители Лагранжа
.
Следовательно,
.
Перепишем условие задачи, введя приращение 
:
;
. 
Из первых трех уравнений получаем 
и подставим в последнее уравнение:
, 
.
.
.
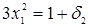Возьмем, например, 
.
С другой стороны,
.
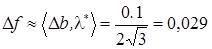Аналогично для 
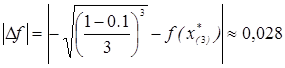и 
.
Решить задачу максимизации квадратичной функции
при условиях 
15 и 
1,2,3.
Перепишем условие следующим образом:
Функция Лагранжа имеет вид
.
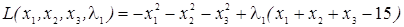Необходимые и достаточные условия минимума:
, 
, 
,
, 
, 
.
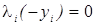Получаем систему уравнений и неравенств:
Для решения промежуточной задачи ЛП воспользуемся средствами MS Excel. Введем формулы, соответствующие системе (рис.2), и начальное приближение для решения системы уравнений (рис.3).
Рис.2. Ввод данных задачи
Рис.3. Задание начального приближения
Заполним поля диалога "Поиск решения" (рис.4).
Рис.4. Экранная форма "Поиск решения"
В окне "Параметры" установим флажок "Неотрицательные значения".
В результате решения найдена седловая точка функции Лагранжа
(х*,λ*) = (15; 0; 0; 30) (рис.5).
Рис.5. Результаты поиска решения.
Оптимальное решение задачи: х* (15; 0; 0), f (x*) = 225.
Задания для лабораторного практикума
Решить задачу минимизации функции методом множителей Лагранжа.
|
|
|
Решить ЗНП методом седловой точки. Промежуточную задачу решения СЛАУ решить, используя EXCEL.
1. 
.
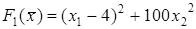2. 
.
3. 
.
4. 
.
5. 
.
6. 
.
7. 
.
8. 
.
Ограничения (для всех вариантов):
.
Контрольные вопросы:
Активные и пассивные ограничения. Регулярная задача.
Теорема Куна-Такера.
Достаточные условия минимума в задачах математического программирования.
Седловая точка.
Метод седловой точки для задачи квадратичного программирования.
Библиографический список
1. Стандарт предприятия: Общие требования и правила оформления дипломных и курсовых проектов (работ): СТП УГТУ - УПИ 1 - 96. Екатеринбург, 1996.
2. Акулич И.Л. Математическое программирование в примерах и задачах / И.Л. Акулич. М.: Высшая школа, 1993.335 с.
3. Аттетков А.В. Методы оптимизации / А.В. Аттетков, С.В. Галкин,
4. В.С. Зарубин. М.: МГТУ, 2004.432 с.
5. Васильев В.П. Численные методы решения экстремальных задач / В.П. Васильев. М.: Наука, 1980.518 с.
6. Габасов Р. Методы оптимизации / Р. Габасов, Ф.М. Кириллова. Минск: БГУ, 1981.350 с.
7. Дьяконов В. Matlab: учебный курс / В. Дьяконов. СПб.: Питер, 2001.560 с.
8. Еремин И.И. / И.И. Еремин, Н.Н. Астафьев. М.: Наука, 1976.192 с.
9. Пантелеев А.В. Методы оптимизации в примерах и задачах /
10. А.В. Пантелеев, Т.А. Летова. М.: Высшая школа, 2005.544 с.
11. МЕТОДЫ ОПТИМИЗАЦИИ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ: методические указания к лабораторным работам / сост. С.Д. Чернина. Екатеринбург: УГТУ-УПИ, 2007.36 с.
Приложение
Рекомендации по использованию EXCEL и MATLAB
Построение графиков
Для построения графика функции y= f (x1, x2) могут быть использованы следующие инструменты:
1. В EXCEL - Мастер диаграмм, подтип Поверхность.
а. Используя автозаполнение, на листе EXCEL в столбец А и первую строку с выбранным шагом ввести соответственно значения переменных x1 и x2, для которых будут вычисляться значения функции.
б. В ячейку В2 ввести выражение для вычисления функции f (x1, x2) в точках $A2, B$1 (знак $ - признак абсолютной адресации, при которой будут зафиксированы первый столбец - перебор значений переменной x 1 и первая строка - перебор значений переменной x2) и нажать одновременно три клавиши Ctrl, Shift, Enter, поскольку формула используется для обработки массивов. В строке формул должны появиться фигурные скобки.
|
|
|
в. Выделить ячейку В2 и, протянув маркер заполнения сначала вниз, пробегая все ячейки, заполненные в столбце А, а затем вправо, пробегая все ячейки, заполненные в строке 1, заполнить массив значений функции в узловых точках области построения графика.
г. На вкладке "Стандартные" Мастера диаграмм выбрать подтип Поверхность. Поверхностная диаграмма дает трехмерное изображение функции, а контурная диаграмма представляет вид сверху на поверхностную диаграмму и является аналогом линий уровня исследуемой функции.
2. В MATLAB - функции plot3, mesh, surf, surfl.
а. С помощью функции meshgrid получить двумерные массивы координат узловых точек области построения графика: u= a: ∆1: b; v = c: ∆2: d; [ x,y ] =meshgrid (u,v).
б. Задать исследуемую функцию: f = f (х, у).
в. Применяя указанные выше функции, получить трехмерное изображение: plot3 (x,y,f) или mesh (x,y,f), surf (x,y,f), surfl (x,y,f).
Действия с матрицами
Для нахождения собственных значений и собственных векторов матрицы Гессе могут быть использованы следующие инструменты MATLAB:
λ = eig (a) - функция eig (a) возвращает собственные значения заданной матрицы a. Пример задания матрицы 4х4: a = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1];
[ v, d ] = eig (a) - при таком обращении функция возвращает собственные векторы v и собственные значения как элементы диагональной матрицы d.
Для нахождения матрицы, обратной матрице Гессе, могут быть использованы следующие инструменты:
В EXCEL - функция МОБР возвращает обратную матрицу для матрицы, хранящейся в массиве.
В MATLAB - функция y=inv (a) возвращает обратную матрицу для матрицы a.
[1] Лабораторная работа выполнена студентом Коневым С.
|
|
|
