 |
Порядок выполнения лабораторной работы
|
|
|
|
Записать необходимые условия экстремума. Аналитически или используя прикладные пакеты найти стационарные точки.
Проверить выполнение достаточных условий экстремума в найденных стационарных точках. Найти глобальный минимум функции. Оценить обусловленность задачи в точке минимума и овражность графика в окрестности точки минимума. Сделать предварительный вывод о работоспособности избранного численного метода.
Выбрать пакет, в котором будет строиться график. Рекомендации приведены в приложении. Построить график функции, задавая пределы изменения координат с учетом аналитически найденных точек минимума - максимума.
Выбрать несколько начальных точек для реализации численного метода. Задать критерий завершения итерационного процесса. Найти минимум. Сравнить результаты с аналитически найденным значением глобального минимума. Исследовать сходимость алгоритма, фиксируя точность определения минимума, количество итераций метода и количество вычислений минимизируемой функции в зависимости от задаваемой точности поиска. Результатом выполнения данного пункта должны быть выводы об объёме вычислений в зависимости от задаваемой точности и начального приближения.
3. Пример выполнения лабораторной работы [1]
Функция: 
min, x0 = (-2,-2).
Методы: градиентного спуска и Ньютона.
Решение: 1. Построим график функции и линии уровня (рис.1).
Примечание: при построении графика используется среда MathCAD.
Рис.1. Графики функции 
и линий уровня
2. Решим задачу минимизации аналитически.
Система для нахождения стационарных точек из условия равенства нулю градиента имеет вид
Если x1 x2 =0, тоиз системы следует, что x1 =0 и x2 =0.
|
|
|
Первая стационарная точка - A0 (0; 0).
Если
x1 x2 ≠0, то
Подставим х1 в первое уравнение:
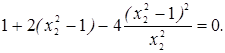
Введем замену
:
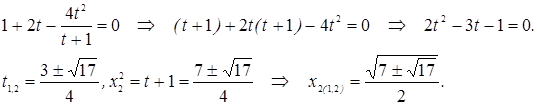
Обозначим
, 
.
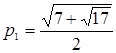Получаем остальные стационарные точки:
;
;
;
.
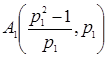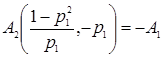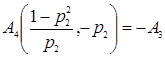Приближенные числовые координаты найденных точек:
А0 (0; 0), А1 (1.068; 1.668), А2 (-1.068; - 1.668), А3 (-0.331; 0.848), А4 (0.331;0.848).
Построим и исследуем на знакоопределенность матрицу Гессе в точках А0,…, А4.
;
.
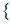
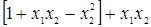H (A0 ( 0; 0)) =0
(требуется дополнительное исследование точки).
Анализ поведения функции в окрестности точки A0 ( 0; 0 ) показывает, что, придавая х1 положительное и отрицательное значение при любом х2, можно получить соответственно положительное и отрицательное значение функции. Таким образом, A0 ( 0; 0 ) не является ни точкой локального минимума, ни точкой локального максимума.
Н (А1 (1,068; 1,668)) ≈ 
, матрица отрицательно определена, в точке А1 локальный максимум.
Н (А2 (-1,068; - 1,668)) ≈ 
, матрица положительно определена, в точке А2 локальный минимум.
Н (А3 (-0,331; 0,848)) ≈ 
, матрица положительно определена, в точке А3 локальный минимум.
Н (А4 (0,331; - 0,848)) ≈ 
, матрица отрицательно определена, в точке А4 локальный максимум.
Точками глобального экстремума являются А1 (1,068; 1,668) - глобальный максимум, f (A1) ≈1,801; А2 (- 1,068; - 1,668) - глобальный минимум, f (A2) ≈≈ - 1,801.
3. Остальные задания реализованы на языке СИ, для чего написаны классы для работы с векторами и матрицами (Cvector и Cmatrix) и использующее их приложение. В методе наискорейшего спуска для одномерной минимизации используется метод золотого сечения. Для отыскания собственных чисел матрицы Гессе применяется метод Якоби, для построения обратной матрицы - метод Жордана-Гаусса.
В начале работы программа выводит информацию о стационарных точках:
Stationary dots:
x1x2f (x1,x2) Extreme
1.0678901.6675661.801131LOC MAX
1.067890-1.667566-1.801131LOC MIN
0.3310770.848071-0.144426LOC MIN
|
|
|
0.331077-0.8480710.144426LOC MAX
GLOBAL MIN: x (-1.067890, - 1.667566)
f (x) = - 1.801131
GLOBAL MAX: x (1.067890, 1.667566)
f (x) = 1.801131
Затем устанавливается начальная точка x0 (-2,-2), функция исследуется на выпуклость/вогнутость в этой точке, выводится число обусловленности матрицы Гессе:
x0 (-2.000000, - 2.000000) Hessian: Alternating sign
f (x0) = - 0.398297
cond H (x0) = 4.751665
Таким образом, квадратичная форма, соответствующая матрице 
, является знакопеременной. Функция не является овражной в окрестности точки, и допустимо применение метода градиентного спуска.
Далее запускается метод наискорейшего градиентного спуска, и выполняются две итерации.
Steepest descent method:
x2 (-1.200031, - 1.706888) Hessian: Convex
grad_f (x2) = (-0.963083, 0.275166)
f (x2) = - 1.741440
В результате двух итераций мы получили точку, достаточно близкую к точке глобального минимума.
Теперь из точки (-2; - 2) стартует метод Ньютона с поправкой гессиана. Результат двух итераций:
Newton method:
x2 (-2.735431, - 2.306328) Hessian: Alternating sign
grad_f (x2) = (-0.110421, 0.031948)
f (x2) = - 0.018516
Видно, что метод расходится. Начальная точка выбрана неудачно. Увеличение числа итераций приводит к дальнейшему расхождению метода. Это объясняется тем, что в начальной точке функция не является выпуклой. Анализируя линии уровня функции, выберем начальную точку ближе к оптимальной. Например, (-1; - 2):
x0 (-1.000000, - 2.000000) Hessian: Convex,
f (x0) = - 1.471518, cond H (x0) = 3.786885
Newton method:
x2 (-1.047041, - 1.722604) Hessian: Convex
grad_f (x2) = (0.379214, - 0.339841)
f (x2) = - 1.787758
Как в начальной, так и в конечной точке функция является выпуклой. За две итерации мы приблизились к точке А 2 (-1,068; - 1,668).
Теперь возьмем начальную точку еще ближе к А 2, например (-1; - 1,5):
x0 (-1.000000, - 1.500000) Hessian: Convex
f (x0) = - 1.752302
cond H (x0) = 3.857905
Newton method:
x2 (-1.067889, - 1.667566) Hessian: Convex
grad_f (x2) = (0.000000, 0.000000)
f (x2) = - 1.801131
Метод Ньютона достиг точки глобального минимума, об этом говорит практически нулевой вектор-градиент.
Точное значение 
отличается от полученного методом Ньютона 
на 4,729∙10-7 (по модулю).
Выводы.
В лабораторной работе проведено исследование заданной функции на глобальный экстремум с использованием аналитических преобразований, графика функции и разработанного приложения на языке C++.
С помощью метода градиентного спуска удалось улучшить целевую функцию. Выбор точки x0 (-2,-2) в качестве начальной для реализации метода Ньютона оказался неудачным, так как матрица Гессе в ней не является положительно определенной. Замена начальной точки на более подходящую для данного метода позволила за две итерации прийти в точку глобального минимума. Полученные результаты хорошо согласуются с теорией.
|
|
|
Разработанные классы Cvector и Cmatrix могут применяться в будущих проектах.
|
|
|
