 |
Теоретический обзор. Решение задачи минимизации со смешанными ограничениями
|
|
|
|
Общая задача нахождения экстремума функции при наличии ограничений - равенств и ограничений - неравенств записывается в следующем виде:
f (x) → extr, (6)
x Î X = { x Î En: gi (x) ≤0, i =1,2,…, r; gi (x) =0, i = r +1, …, m, m - r < n },
где среди функций f (x) и gi (x) могут быть нелинейные.
Активные ограничения - неравенства в точке х* ─ это ограничения, которые выполняются в данной точке в виде равенства.
Пассивные ограничения - неравенства в точке х* ─ это ограничения, которые выполняются в данной точке в виде строгого неравенства.
Если градиенты активных ограничений-неравенств и ограничений-равенств в точке х* линейно независимы, то говорят, что в оптимальной точке выполнено условие регулярности.
Обобщенная функция Лагранжа для задачи со смешанными ограничениями задается как
L (x, λ 0, λ ) = λ 0 f (x) +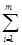 
λ i gi (x). ( 7)
При выполнении условия регулярности λ 0 ≠0 и можно положить этот коэффициент равным 1.
Теорема Куна - Таккера (дифференциальная форма необходимого условия минимума). Пусть точка х* - точка локального минимума в задаче математического программирования (6), функции f, gr+1,…, gm дважды непрерывно дифференцируемы в точке х, функции g1,…, gr дважды непрерывно дифференцируемы в некоторой окрестности точки x. Тогда существует число 
и вектор 
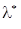такие, что выполняются следующие условия:
условие стационарности обобщенной функции Лагранжа по х:
grad xL (x*, , 
) =0;
условие нетривиальности:
2+ 2>0,т.е. хотя бы один из множителей Лагранжа отличен от нуля;
условие неотрицательности:
≥0, 
≥0, i =1, …, r,
т.е. множители Лагранжа, соответствующие целевой функции и ограничениям - неравенствам, неотрицательны;
|
|
|
условия дополняющей нежесткости:
gi (x *) =0, i =1, 2, …, r.
Если при этом выполнено условие регулярности, то для выпуклых функций f, gr+1,…, gm и линейных функций g1,…, gr условия теоремы Куна - Таккера являются одновременно необходимыми и достаточными условиями глобального минимума.
Достаточное условие минимума первого порядка.
Пусть имеется точка (х*, ), удовлетворяющая условию стационарности обобщенной функции Лагранжа по х при 
≠0, суммарное число активных ограничений-неравенств в точке х* и ограничений-равенств совпадает с числом переменных n. Если 
>0 для всех активных ограничений gj (x), то точка х* - точка условного локального минимума в задаче (6).
Достаточное условие минимума второго порядка.
Пусть имеется точка (х*, ), удовлетворяющая условию стационарности обобщенной функции Лагранжа по х при 
≠0. Если в этой точке d 2 L (х*, 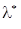) >0 для всех ненулевых dx таких, что для активных в точке х* ограничений-неравенств dgj (x*) =0, >0 и dgj (x*) ≤0, =0, то точка х* является точкой локального минимума.
Общая схема решения задачи условной минимизации функции:
Составляется обобщенная функция Лагранжа вида (7).
Выписываются необходимые условия минимума, сформулированные в теореме Куна - Таккера. К этим условиям добавляются ограничения, задающие допустимое множество Х. Полученная система алгебраических уравнений и неравенств используется для поиска условно-стационарных (подозрительных на экстремум) точек. Целесообразно проанализировать отдельно случаи λ0=0 и λ0=1 (или λ0 - любое положительное число). Однако если выполнено одно из условий регулярности, то вариант λ0=0 рассматривать не надо.
В найденных точках проверяется выполнение достаточных условий минимума и проводится анализ на глобальный экстремум.
Чувствительность решения ЗНП.
Множители Лагранжа могут быть использованы для оценивания влияния малых изменений правых частей ограничений на оптимальное решение задачи нелинейного программирования. Пусть х *= х * (b) - решение ЗНП
|
|
|
f (x) → min, (8)
x Î X= { x Î En: gi (x) ≤ bi, i =1,2,…, m; х ≥0}
при некотором векторе b свободных членов в ограничениях - неравенствах, а v (b) соответственно значение целевой функции при этом решении ЗНП, т.е. v (b) = f (x*). Тогда справедлива следующая оценка изменения целевой функции: ∆ v = f (b+∆ b) - f (b) при изменении вектора b на некоторый малый вектор-приращение ∆ b:
∆ f ≈ (∆ b, λ *), (9)
где λ * - вектор множителей Лагранжа, соответствующий решению х* (b).
|
|
|
