 |
Обобщающие статистические показатели. Абсолютные и относительные величины.
|
|
|
|
Пример 1.
Из общей численности населения России, равной на конец 1985г. 143,8 млн. человек, 104,1 млн. составляли городские жители, 39,7 млн. — сельские. Рассчитав относительные величины структуры, можно определить удельные веса (или доли городских и сельских жителей) в общей численности населения страны, т.е. структуру населения по месту жительства:
городское — (104,1 / 143,8) *100 = 72,4:
сельское — (39,7 / 143,8) *100 = 27,6.
Спустя 6 лет, численность населения страны составила 148,7 млн., в том числе: городских жителей — 109,7 млн., сельских — 39,0 млн. Исходя из этих данных исчисляются показатели структуры населения:
городское — (109,7 / 148,7) *100 = 73,8:
сельское — (39,0 / 148,7) *100 = 26,2.
Сравнив состав населения страны в 1985г. и 1991г., можно сделать вывод о том, что происходит увеличение удельного веса городских жителей.
Пример 2.
Реализация хлопчатобумажных тканей секцией универмага составила в январе 3956 тыс. руб., в феврале — 4200 тыс. руб., в марте — 4700 тыс. руб.
Темпы роста:
базисные (база — уровень реализации в январе)
 = 4200:3950*100 = 106,3%
= 4200:3950*100 = 106,3%
 = 4700:3950*100 = 118,9%
= 4700:3950*100 = 118,9%
цепные
 = 4200:3950*100 = 106,3%
= 4200:3950*100 = 106,3%
 = 4700:4200*100 = 111,9%
= 4700:4200*100 = 111,9%
Пример 3.
По данным Всесоюзной переписи населения 1989г. численность населения Москвы составила 8967 тыс., а численность населения Санкт-Петербурга — 5020 тыс. человек.
Рассчитаем относительную величину сравнения, приняв за базу сравнения численность жителей Санкт-Петербурга: 8967 / 5020 = 1,79. Следовательно, численность населения Москвы в 1,79 раза больше, чем в Санкт-Петербурге.
Пример 4.
На начало года численность специалистов с высшим образованием, занятых в ассоциации “Торговый дом”, составила 53 человека, а численность специалистов со средним специальным образованием — 106 человек. Приняв за базу сравнения численность специалистов с высшим образованием, рассчитаем относительную величину координации: 106/53=2,0/1,0, т.е. на двух специалистов со средним специальным образованием приходится один специалист с высшим образованием.
|
|
|
СРЕДНИЕ ВЕЛИЧИНЫ
Имеются следующие данные о лабораторных испытаниях 1000 образцов пряжи на крепость
| Крепость пряжи, г | Число образцов |
| до 180 | |
| 180-200 | |
| 200-220 | |
| 220-240 | |
| 240 и более |
Средняя крепость пряжи составляет:

Ответ: 213,6.
Пример 1.
Имеются следующие данные о производстве рабочими продукции А за смену:
| № раб. | ||||||||||
| Выпущено изделий за смену |
В данном примере варьирующий признак - выпуск продукции за смену.
Численные значения признака (16, 17 и т. д.) называют вариантами. Определим среднюю выработку продукции рабочими данной группы:

Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т.е. данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.
Пример 2.
Имеются следующие данные о заработной плате рабочих - сдельщиков:
| Месячная з/п (варианта - х), руб. | Число рабочих, n | xn |
| х = 110 | n = 2 | |
| х = 130 | n = 6 | |
| х = 160 | n = 16 | |
| х = 190 | n = 12 | |
| х = 220 | n = 14 | |
| ИТОГО |
Вычислим среднюю заработную плату одного рабочего  в руб.:
в руб.:

Пример 3.
Имеются следующие данные:
| Группы рабочих по количеству произведенной продукции за смену, шт. | Число рабочих, n | Середина интервала, х | хn |
| 3 — 5 | |||
| 5 — 7 | |||
| 7 — 9 | |||
| 9 — 11 | |||
| 11 — 13 | |||
| ИТОГО |
Исчислим среднюю выработку продукции одним рабочим за смену Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:
|
|
|

Для первой группы дискретная величина х будет равна:
(3 + 5) / 2 = 4
Дальнейший расчет производится обычным методом определения средней арифметической взвешенной:

Итак, все рабочие произвели 750 шт. изделий за смену, а каждый в среднем произвел 7,5 шт.
Пример 5.
Определим средний процент выполнения плана по выпуску продукции по группе заводов на основании следующих данных:
| Номер завода | Выпуск продукции по плану, млн.руб. | Выполнение плана, % |
| ИТОГО | — |
| или 102,4% |

Пример 6.
Бригада токарей была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15 мин., третий - 11, четвертый - 16 и пятый - 14 мин. Определите среднее время, необходимое на изготовление одной детали.
На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:

Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим соотношением:

Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:

Это же решение можно представить иначе:

Пример 7.
Издержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными:
| Номер завода | Издержки производства, тыс.руб. | Себестоимость единицы продукции, руб. |
Исчислим среднюю себестоимость изделия по трем заводам.

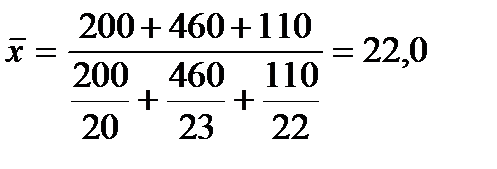 руб.
руб.
МОДА, МЕДИАНА.
Задача. Имеются данные о распределении 100 семей по количеству детей в семье:
| Число детей | Количество семей |
| Итого |
Мода равна 1.
Пример 8.
Распределение проданной обуви по размерам характеризуется следующими показателями:
|
|
|
| размер обуви | и выше | ||||||||||
| число пар, в % к итогу | — | — |
В этом ряду распределения мода равна 41. Именно этот размер обуви пользовался наибольшим спросом покупателей.
Пример 9.
Распределение предприятий по численности промышленно - производственного персонала характеризуется следующими данными:
| Группы предприятий по числу работающих, чел | Число предприятий |
| 100 — 200 | |
| 200 — 300 | |
| 300 — 400 | |
| 400 — 500 | |
| 500 — 600 | |
| 600 — 700 | |
| 700 — 800 | |
| ИТОГО |
В этой задаче наибольшее число предприятий (30) имеет численность работающих от 400 до 500 человек. Следовательно, этот интервал является модальным интервалом ряда распределения.
Введем следующие обозначения:
 =400,
=400,  =100,
=100,  =30,
=30,  =7,
=7,  =19
=19
Подставим эти значения в формулу моды и произведем вычисления:
| чел. |

Пример 10.
Определим медиану заработной платы рабочих.
| Месячная з/п, руб. | Число рабочих | Сумма накопительных частот |
| 8 (2+6) | ||
| 24 (8+16) | ||
| — | ||
| — | ||
Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину. В нашем примере сумма частот составила ее половина - 20.
Накопленная сумма частот ряда получилась равной Варианта, соответствующая этой сумме, т.е. 160 руб., и есть медиана ряда.
Если же сумма накопленных частот против одной из вариант равна точно половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.
Пример 11.
| Месячная з/п, руб. | Число рабочих | Сумма накопительных частот |
| 8 (2+6) | ||
| 20 (8+12) | ||
| — | ||
| — | ||
Медиана будет равна:
Ме = (150 + 170) / 2 = 160 руб.
Пример 12.
| Группы предприятий по числу рабочих | Число предприятий | Сумма накопительных частот |
| 100 — 200 | ||
| 200 — 300 | 4 (1+3) | |
| 300 — 400 | 11 (4+7) | |
| 400 — 500 | 41 (11+30) | |
| 500 — 600 | — | |
| 600 — 700 | — | |
| 700 — 800 | — | |
| ИТОГО |
|
|
|
Определим прежде всего медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений (41), соответствует интервалу 400 - 500. Это и есть медианный интервал, в котором находится медиана. Определим ее значение по приведенной выше формуле.
Известно, что:

Следовательно,

ПОКАЗАТЕЛИ ВАРИАЦИИ
Пример 1.
Группы предприятий по объему товарооборота, млн.руб. 
| Число предприятий

|
| 90 — 100 | |
| 100 — 110 | |
| 110 — 120 | |
| 120 — 130 | |
| ИТОГО |
Определяем показатель размаха вариации:
R = 130 – 90 = 40 млн. руб.
Пример 2.
| Табельный номер рабочего | 
| 
| /  / /
|
| - 8 | |||
| - 7 | |||
| Итого |
d=  =
= 
Пример 3.
Произведено продукции одним рабочим, шт.
( варианта) варианта)
| Число рабочих, 
| 
| 
| 
| 
|
| -2 | |||||
| -1 | |||||
| ИТОГО |
Исчислим среднюю арифметическую взвешенную:
 шт.
шт.
Значения отклонений от средней и их квадратов представлены в таблице 6.3. Определим дисперсию:
 =1,48
=1,48
Среднее квадратическое отклонение будет равно:
 шт.
шт.
Пример 4.
Покажем расчет дисперсии для интервального ряда на данных о распределении посевной площади колхоза по урожайности пшеницы:
| Урожайность пшеницы, ц/га | Посевная площадь, га | 
| 
| 
| 
| 
|
| 14 - 16 | -3,4 | 11,56 | ||||
| 16 - 18 | -1,4 | 1,96 | ||||
| 18 - 20 | 0,6 | 0,36 | ||||
| 20 - 22 | 2,6 | 6,76 | ||||
| ИТОГО |
Средняя арифметическая равна:
 ц с 1га.
ц с 1га.
Исчислим дисперсию:
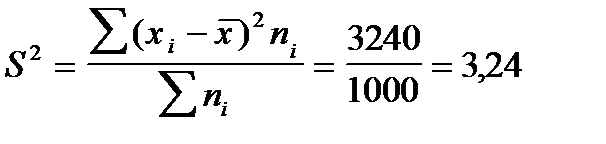
|
|
|


