 |
Однофазные трансформаторы. Холостой ход однофазного трансформатора
|
|
|
|
Ток холостого хода
При синусоидальном напряжении и потоке, ток холостого хода имеет несинусоидальную форму, за счет насыщения железа в области амплитуды потока.
Рассмотрим, какие потоки и ЭДС в однофазном трансформаторе.
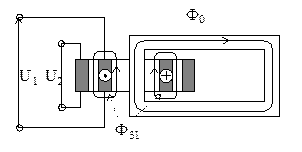
Ф0 ® E1, E2 ФS1 ® E2S
ЭДС рассеяния
e1S = -LS(dl0/dt) = -LS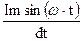 
=
=-Im wLS coswt
ЭДС рассеяния в комплексной
форме (wLS = x1)
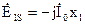
В первой обмотке три ЭДС ®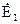 
, 
, 
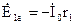
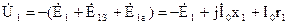
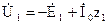
Фаза ЭДС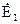
E1 = -W1(dФ/dt) = -W 
= wW1Фm sin(wt - p/2), (wW1Фm = E1m)
Действующие значения ЭДС обмотки
E1max = wW1Фm = 2pf1W1Фm
E1 =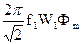 
E1 = 4,44 f1W1Фm
E2 = 4,44 f1W2Фm
E1/E2 = k U1/U2 = k
При x x
U2 = E2
U1» E1
Потери при холостом ходе трансформатора
Мощность, потребляемая трансформатором при холостом ходе идет на покрытие в обмотках и стали: P0 = p эл1 + Pмагн
pэл1 = 1 ¸ 2% от P0
Поэтому, мощность при холостом ходе трансформатора идет в основном на покрытие потерь в стали (гистерезис и вихревые токи).
pr = sr(f/100)B2
Pосн мг
pb = sвх(f/100)2B2
pдоб = 15 ¸ 20% Pосн мг Итак P0 = (1,15 ¸ 1,2) Pмго
Схема замещения трансформатора при холостом ходе
Исследование работы трансформатора упрощается, если действительный трансформатор, в котором обмотки связаны между собой электромагнитно, заменить схемой элементы которой, связаны между собой только электрически. Такая схема называется схемой замещения трансформатора. Схема замещения должна удовлетворять основным уравнениям ЭДС и МДС трансформатора.
Цепь ab - цепь намагничивания
zm, rm, xm параметры цепи намагничивания.
1.2.4.Определение параметров экспериментально zm, xm, rm
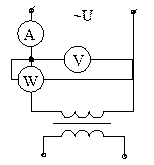Для определения параметров измеряются:
P0, U, I0 тогда
z0 =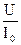 
; r0 = 
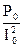; x0 =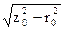 
т. к. r1 << rm x1 << xm, то
zm» z0 = 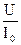; rm» r0 = 
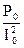; xm» x0 =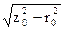
|
|
|
Из опыта холостого хода определяем:
1. параметры цепи намагничивания;
2. потери в стали;
3. определяем коэффициент трансформации.
Работа однофазного трансформатора под нагрузкой
Приведение параметров вторичной обмотки трансформатора к первичной.
Так как в общем случае W1 ¹ W2, E1 ¹ E2, и т.д. соответственно разным W и E соответствуют разные параметры. Это затрудняет производить количественный анализ процессов происходящих в трансформаторе и построение векторных диаграмм. Обычно приводят параметры вторичной обмотки к числу витков W1, поэтому E’2 = E1
1) E2 ® E¢2; 
;
E¢2 = E2×k
2) I2 ® I¢2; E¢2I¢2 = E2I2; I¢2= 
= 
;
I¢2 = I2/k
3) r2 ® r¢2;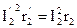 
; 
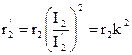
4) x2 º L2 º W22;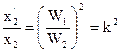 
x’2 = x2×k2; z’2 = z2×k2
Далее в схемах замещения и векторных диаграммах будем использовать приведенные параметры.
Физические процессы в трансформаторе при нагрузке
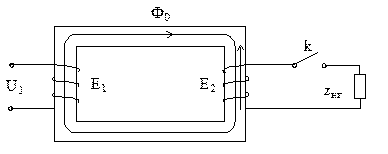
При разомкнутом ключе k – xx.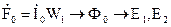 
При замыкании ключа k под действием ЭДС E2 протекает ток I2
Вторичный ток I2 по закону Ленца создает поток встречный потоку Ф0. Суммарный поток уменьшается, уменьшается E1 и из сети будет протекать такой дополнительный ток, который скомпенсирует поток вторичной обмотки и поток будет равен потоку при x.x.
Вторичная обмотка создает н.с. F2 = I2W2
Намагничивающая сила трансформатора при нагрузке
; 
; 
.
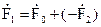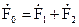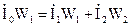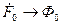
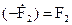
Для сохранения неизменности потока необходимо чтобы при нагрузке сумма ампер-витков первичной и вторичной обмоток трансформатора по величине и по фазе была равна ампер- виткам трансформатора при холостом ходе.
; 
; 
.
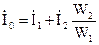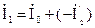Основной поток Ф0 создается малой намагничивающей силой I0W1, но при малом магнитном сопротивлении, достигает большой величины. Поток рассеяния ФS создается большой намагничивающей силой – I1W1, но т.к. он проходит в основном по маслу, то величина его мала. Далее построим векторную диаграмму трансформатора при нагрузке.
|
|
|
Векторная диаграмма трансформатора при нагрузке
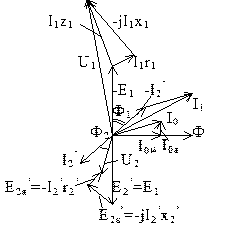
Запишем основные уравнения ЭДС и токов.
1) 
2) 
Ф0 ® 
3) 
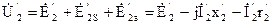
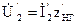
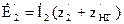
На основе этих уравнений строится векторная диаграмма.
|
|
|
