 |
Пустое и универсальное множества
|
|
|
|
Определение 1.1. В теории множеств отдельно вводится множество, которое не содержит ни одного элемента. Такое множество называется пустым и обозначается символом Æ.
В любой конкретной задаче приходится иметь дело только с подмножествами некоторого, фиксированного для данной задачи, множества. Его принято называть универсальным и обозначать символом U.
Например, при сборке некоторого изделия универсальным множеством естественно назвать множество всех деталей и сборочных элементов, из которых это изделие состоит.
Если мы рассматриваем множества, связанные с какими-нибудь фигурами на плоскости, то в качестве универсального множества можно выбрать множество всех точек плоскости.
Определение 1.2. Два множества A и B называются равными (A = B), если они состоят из одних и тех же элементов. Поэтому несуществен порядок записи в фигурных скобках элементов множества, задаваемого списком, т.е. { a, b, c } = { a, c, b }.
Определение 1.3. Множество A называется подмножеством множества B, если любой элемент множества A принадлежит множеству B. При этом пишут A Ì B, где " Ì " есть знак вложения подмножества. Из определения следует, что для любого множества A справедливы, как минимум, два вложения A Ì A и A Ì U.
Определение 1.4. Если A Ì B и A ¹ B, A ¹ Æ, то A называется
собственным подмножеством множества B. В этом случае B содержит хотя бы один элемент, не принадлежащий A.
В теории множеств, по определению, полагают, что пустое множество является подмножеством любого множества: Æ ÌA.
Пустое множество и само множество A называются несобственными подмножествами множества A.
При графическом изображении множеств удобно использовать диаграммы Венна, на которых универсальное множество обычно представляют в виде прямоугольника, а остальные множества в виде овалов, заключенных внутри этого прямоугольника (рис 1.1).
|
|
|
Определение 1.5. Объединением множеств A и B (обозначение A ÈB) называется множество элементов x таких, что x принадлежит хотя бы одному из двух множеств A или B (рис 1.2). Символически это можно записать следующим образом:
AÈ B = {x|x Î A или x Î B}.
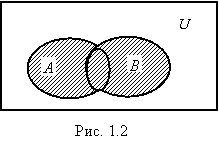
Определение 1.6. Пересечением множеств A и B (обозначение A ÈB) называется множество, состоящее из элементов x, которые принадлежат и множеству A и множеству B (рис. 1.3):
AÈ B = { x|x Î A и x Î B}.
Определение 1.7. Разностью множеств A и B называется множество всех тех элементов множества A, которые не принадлежат множеству B (рис. 1.4):
A\B = { x|x Î A и x Î B}.
Определение 1.8. Симметрической разностью множеств A и B называется множество A D B = (A\B) È (B\A) (рис. 1.5).
Определение 1.9. Абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, т.е. множество A = U\A, где U - универсальное множество (рис. 1.6).
В дальнейшем вместо термина "абсолютное дополнение" мы будем употреблять термин "дополнение".
Пример 1.1. Если U = { a, b, c, d, e, f, g, h }, A = { c, d, e }, B = { a, c, e, f, h }, то
|
|
Свойства операций
Для любых множеств A,B,C выполняются следующие тождества:
1. A È B = B ÈA, AÇ B = BÇ A
(коммутативность объединения и пересечения);
2. A È (B ÈC) = (A È B) ÈC, A Ç (B ÇC) = (AÇ B) Ç C
(ассоциативность объединения и пересечения);
3. A Ç (B ÈC) = (A ÇB) È (AÇC),
A È (BÇ C) = (A ÈB) Ç (A ÈC)
(дистрибутивность);
Функция
Понятие функции
Пусть заданы два множества Х и Y. Если каждому элементу х 
Х поставлен в соответствие один и только один элемент у 
У, обозначаемый f(х), и если каждый элемент у У при этом оказывается поставлен в соответствие хотя бы одному элементу х Х, то говорится, что на множестве Х задана однозначная функция у = f(х). Множество Х называется областью ее определения, а множество Y - множество ее значений. Элемент х Х называется аргументом или независимой переменной, а элементы у Y - значениями функции, или зависимой переменной..
|
|
|
Рис. 2.1.
Элементы х и у рассматриваемых множеств могут иметь совершенно произвольную природу. Если значениями функции являются не числа, а другие элементы, часто вместо слова “функция” употребляют слово “отображение”.
Для того, чтобы задать функцию f, надо знать:
1. Х - область определения (существования);
2. Y - область значений;
3. Закон соответствия, по которому определяется элемент у Y, соответствующий х Х.
Способы задания функций.
1. Если функция задана выражением при помощи формулы, то говорят, что она задана аналитически, Для этого используется некоторый запас изученных и специально обозначенных функций, алгебраические действия и предельный переход.
Например, 
.
Здесь 
- это совокупность действий, которые нужно выполнить в определенном порядке над значениями аргумента х, чтобы получить соответствующее значение функции y (или, то же самое, 
).
Примеры:
1.
2. Функция Дирихле:
3.
2. Функцию можно задавать таблично, т.е. для некоторых значений х указать соответствующие значения переменной y.
| X | x1 | x2 | ... | xi | ... | xn |
| Y | y1 | y2 | ... | yi | ... | yn |
Данные такой таблицы могут быть получены как экспериментально, так и с помощью математических расчетов.
Примерами табличного задания функций могут быть: логарифмические таблицы, таблицы тригонометрических функций.
3. Аналитический и табличный способы задания функций страдают отсутствием наглядности.
(*)
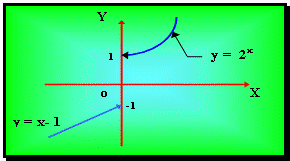Рис. 2.3.
|
Графический способ задания функции - это геометрическое место точек на плоскости с координатами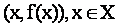 
.
|
|
|
