Понятие функции нескольких переменных.

Рассмотрим вещественные функции, определенные на множестве n-мерного евклидового пространства Rⁿ, значениями которого являются вещественные числа.

Эти функции обозначаются одним символом, например, или указывая аргумент – f(x), или и называются функциями многих переменных. Здесь переменные называются независимыми переменными или аргументами. Совокупность рассматриваемых их значений - областью определения (областью существования).

Областью существования функции двух переменных (х и y), вообще говоря, представляет собой некоторое множество точек плоскости Oxy, т.е.

.

Аналогично для n=3.

Неявные функции

(Один из способов задания функции)

Определение 2.4. Функция у от аргумента х называется неявной, если она задана уравнением вида: F(x,y) = 0, т.е. задана функция F(x,y) двух вещественных аргументов x и y (если они существуют), для которых выполняется (.

Чтобы выразить функцию y в явном виде, достаточно разрешить относительно y. Так как для данного значения аргумента х уравнение может иметь несколько (и даже бесконечное множество) корней y, то в общем случае неявная функция является многозначной.

Например, функция у (у>0), определяемая уравнением , является неявной. Явно заданная функция будет иметь вид: .

Сложные функции

(Один из способов задания функции)

Пусть заданы две функции , , причем область задания функции F содержит область значений функции 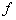, тогда из этой области определения 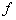ставится в соответствие , где . Эта функция, определенная соответствием , называется сложной функцией, или суперпозицией функций 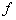и F.

Примеры:

1. ;

2. .

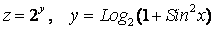- явно задана.

Элементарные функции и их классификация

Функции:

- степенная;

- показательная;

- логарифмическая;

- тригонометрические;

-обратные тригонометрические;

- постоянная.

 

Называются основными элементарными функциями.

Замечание.

Всякая функция, которая может быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических операций и суперпозиций основных элементарных функций, называется просто элементарной функцией.

Элементарные функции обычно делят на классы:

1. Многочлены (полиномы) - это функции вида:

.

Если , то число называется степенью данного полинома.

При многочлен первой степени и называется линейной функцией;

 

2. Класс рациональных функций:

, где - полиномы;

 

3. Алгебраические функции:

Функции, заданные с помощью суперпозиций рациональных функций, степенных с рациональными показателями и четырех арифметических действий, называются алгебраическими.

Например:

.

 

Трансцендентные функции.

Элементарные функции, не являющиеся алгебраическими, называются трансцендентными элементарными функциями.

Функции вида:

- показательная;

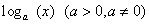- логарифмическая;

- тригонометрические;

- обратные тригонометрические).

 

 

3. Числовая последовательность

Числовая последовательность – функция вида а = f (x), x Î N,где N – множество натуральных чисел (или функция натурального аргумента), обозначается а = f (n)или а ₁, а ₂,…, а_n,…. Значения а ₁, а ₂, а ₃,…называют соответственно первым, вторым, третьим, … членами последовательности.

Например: a_n = n ²

a ₁ = 1² = 1;

a ₂ = 2² = 4;

a ₃ = 3² = 9;… a_n = n ²

Способы задания последовательностей. Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.

1. Последовательность задана аналитически, если задана формула ее n -го члена:

a_n = f (n).

Пример 3.1. a_n = 2 n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

2. Описательныйспособ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.

Пример 3.2. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….

Пример 3.3. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.

3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n -й член последовательности, если известны ее предыдущие члены. В таких случаях указывают формулу, позволяющую выразить n -й член последовательности через предыдущие.

Пример 3.4. a ₁ = 3; a_n = a_{n –1} + 4, если n = 2, 3, 4,….

Здесь a ₁ = 3; a ₂ = 3 + 4 = 7; a ₃ = 7 + 4 = 11; ….

Можно видеть, что полученную в этом примере последовательность можно задать аналитически: a_n = 4 n – 1.

Свойства числовых последовательностей. Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.

Определение. Последовательность { a_n }называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

a ₁ < a ₂ < a ₃ < …< a_n < a_{n +1} < ….

Определение.Последовательность { a_n }называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

a ₁ > a ₂ > a ₃ > … > a_n > a_{n +1} > ….

Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

Определение.Последовательность называется периодической, если существует такое натуральное число T,что начиная с некоторого n, выполняется равенство a_n = a_n+T. Число T называется длиной периода.

Пример 3.6. Последовательность периодична с длиной периода T = 2.

Арифметическая прогрессия. Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.

Таким образом, арифметическая прогрессия – это числовая последовательность { a_n }, заданная рекуррентно соотношениями

a ₁ = a, a_n = a_{n –1} + d (n = 2, 3, 4, …)

(a и d – заданные числа).

Пример 3.7. 1, 3, 5, 7, 9, 11, … – возрастающая арифметическая прогрессия, у которой a ₁ = 1, d = 2.

Пример 3.8. 20, 17, 14, 11, 8, 5, 2, –1, –4,… – убывающая арифметическая прогрессия, у которой a ₁ = 20, d = –3.

Нетрудно найти явное (формульное) выражение a_n через n. Величина очередного элемента возрастает на d по сравнению с предыдущим, таким образом, величина n элемента возрастет навеличину (n – 1) d по сравнению с первым членом арифметической прогрессии, т.е.

a_n = a ₁ + d (n – 1).

Это формула n- го члена арифметической прогрессии.

Геометрическая прогрессия. Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.

Таким образом, геометрическая прогрессия – это числовая последовательность { b_n }, заданная рекуррентно соотношениями

b ₁ = b, b_n = b_{n –1} q (n = 2, 3, 4…).

(b и q – заданные числа, b ¹ 0, q ¹ 0).

Пример 3.9. 2, 6, 18, 54, … – возрастающая геометрическая прогрессия b = 2, q = 3.

Пример 3.10. 2, –2, 2, –2, … – геометрическая прогрессия b = 2, q = –1.

Пример 3.11. 8, 8, 8, 8, … – геометрическая прогрессия b = 8, q = 1.

Геометрическая прогрессия является возрастающей последовательностью, если b ₁ > 0, q > 1, и убывающей, если b ₁ > 0, 0 < q < 1.

Одно из очевидных свойств геометрической прогрессии состоит в том, что если последовательность является геометрической прогрессией, то и последовательность квадратов, т.е.

b ₁², b ₂², b ₃², …, b_n ²,… является геометрической прогрессией, первый член которой равен b ₁², а знаменатель – q ².

Формула n- го члена геометрической прогрессии имеет вид

b_n = b ₁ q^{n– 1}.

Можно получить формулу суммы членов конечной геометрической прогрессии.

.

Это формула суммы n членов геометрической прогрессии для случая, когда a ¹1.

При q = 1 формулу можно не выводить отдельно, очевидно, что в этом случае S_n = a ₁ n.

Геометрической прогрессия названа потому, что в ней каждый член кроме первого, равен среднему геометрическому предыдущего и последующего членов.

Предел последовательности. Пусть есть последовательность { c_n } = {1/ n }.Эту последовательность называют гармонической, поскольку каждый ее член, начиная со второго, есть среднее гармоническое между предыдущим и последующим членами. Среднее геометрическое чисел a и b есть число 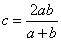, или 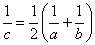. С ростом n все члены геометрической прогрессии убывают и их значение приближается к нулю. В этом случае принято говорить, что при n, стремящемся к бесконечности, данная последовательность сходитсяи нуль есть ее предел. Записывается это так:

.

Строгое определение предела формулируется следующим образом:

Если существует такое число A, что для любого (сколь угодно малого) положительного числа e найдется такое натуральное N (вообще говоря, зависящее от e), что для всех n ³ N будет выполнено неравенство | a_n – A | <e, то говорят, что последовательность{ a_n }сходится и A – ее предел.

Обозначается это так: .

В противном случае последовательность называется расходящейся.

Опираясь на это определение, можно, например, доказать наличие предела A = 0 у гармонической последовательности { c_n } = {1/ n }. Пусть e – сколь угодно малое положительное число. Рассматривается разность

.

Существует ли такое N, что для всех n ³ N выполняется неравенство 1 /N < e? Если взять в качестве N любое натуральное число, превышающее1e /, то для всех n ³ N выполняется неравенство 1 /n £ 1 /N < e,что и требовалось доказать.

Доказать наличие предела у той или иной последовательности иногда бывает очень сложно. Наиболее часто встречающиеся последовательности хорошо изучены и приводятся в справочниках. Имеются важные теоремы, позволяющие сделать вывод о наличии предела у данной последовательности (и даже вычислить его), опираясь на уже изученные последовательности.

Теорема 3.1. Если последовательность имеет предел, то она ограничена.

Теорема 3.2. Если последовательность монотонна и ограничена, то она имеет предел.

Теорема 3.3. Если последовательность { a_n }имеет предел A, то последовательности { ca_n }, { a_n + с}и {| a_n |}имеют пределы cA, A + c, | A | соответственно (здесь c – произвольное число).

Теорема 3.4. Если последовательности { a_n }и { b_n } имеют пределы, равные A и B соответственно, то последовательность { pa_n + qb_n } имеет предел pA + qB.

Теорема 3.5. Если последовательности { a_n } и { b_n }имеют пределы, равные A и B соответственно, то последовательность { a_nb_n } имеет предел AB.

Теорема 3.6. Если последовательности { a_n }и { b_n } имеют пределы, равные A и B соответственно, и, кроме того, b_n ¹ 0 и B ¹ 0, то последовательность { a_n / b_n } имеет предел A/B.

 

Предел функции

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: