Точки непрерывности и точки разрыва функции

Определение 5.1. Функция а, определенная на интервале (а, в) называется непрерывной в точке х_оÎ(а, в)

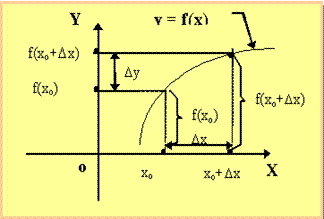Рис.5.1.

Или, если ввести следующие обозначения:

Dx = x₀ - x, Dy = f(x) - f(x₀)

Dx - приращение аргумента;

Dy - приращение функции.

Пусть y = f(x), где х - текущая точка из области определения.

 

Рис.5.2.

Определение 5.2. Функция f(x), определенная на Х, называется непрерывной в точке х = х_о (х_оÎХ).

1) функция в этой точке определена;

2) при Dх = х_о - х ® 0 и,

т.е. функция называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

f(x) - непрерывна в точке х₀ Û " e>0 $ d>0: çx-x₀ç<d, т.е. 0<çDx ç<d, çf(x)-f(x₀)ç=çf(x₀+Dx)-f(x₀)½<e.

Определение 5.3. Функция называется непрерывной на данном множестве Х, если

 

1) она определена на этом множестве, т.е. " х Î Х $ f(x);

 

2) непрерывна в каждой точке этого множества, т.е. " х Î Х справедливо.

Определение 5.4. Точка, в которой нарушается непрерывность функции,

называется точкой разрыва этой функции.

Пусть х₀ - точка разрыва функции f и существуют конечные пределы

f(x₀-0)=, f(x₀+0) =

тогда точка х называется точкой разрыва первого рода.

Величина f(x₀+0) - f(x₀-0) называется скачком функции f в точке х.

Если f(x₀-0)=f(x₀+0), то х называется точкой устранимого разрыва.

Если доопределить функцию таким образом, что

f(x₀)= 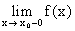= , то получим непрерывную функцию.

Точка разрыва, не являющаяся точкой разрыва первого рода, называется точкой разрыва второго рода. Таким образом, в точках второго рода по крайней мере один из пределов не существует

, .

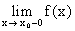Рис.5.3

Основные теоремы о непрерывных функциях

Теорема 5.1. Сумма конечного числа непрерывных функций, определенных на некотором множестве Х, есть функция непрерывная.

Теорема 5.2. Произведение конечного числа непрерывных функций есть функция непрерывная.

С л е д с т в и е. Целый полином Р(х)=а₀+а₁х+... +а_nхⁿ есть функция непрерывная.

Теорема 5.3. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, в которых делитель отличен от нуля.

Теорема 5.4. Непрерывная функция от непрерывной функции есть функция непрерывная.

Теорема 5.5. Если y = f(x) непрерывна и строго монотонна на промежутке <а,b>, то существует обратная функция х = j(y), определенная на промежутке < f(a), f(b) >, причем последняя также монотонна и непрерывна в том же смысле.

Пример. Рассмотреть обратные функции к данным:

а) ; б) .

Рассмотрим теперь непрерывность функции на множествах.

Определение 5.5. Пусть f определена на множестве Е Ì Rⁿ. Функция f называется непрерывной в точке х⁽⁰⁾ Î Е, если " e>0 $ d=d(e):

" х Î Х, удовлетворяющих условию r(х, х⁽⁰⁾) < d выполняется неравенство

çf(x)- f(x⁽⁰⁾) ç < e.

Примем без доказательства ряд простых, но важных теорем.

Теорема 5.6. (Кантора) Функция, непрерывная на ограниченном замкнутом множестве, является равномерно непрерывной.

Определение 5.6. Функция у = f(х), определенная на множестве Е Ì Rⁿ называется равномерно непрерывной на Е, если

" e > 0 $ d = d(e)>0: " x^/, x^// Î E

удовлетворяющих условию r(x^/,x^//)<d будет выполнено неравенство çf(x^/) - f(x^//) ç< e.

Теорема 5.7. (Вейерштрасса) Всякая непрерывная на отрезке функция имеет на этом отрезке как наибольшее, так и наименьшее значение.

Теорема 5.8. (Коши) Если f - непрерывна на [a, b] и f(b) = A, f(b) = B, то

" A < C < B $ x Î [a, b]: f(x) = C.

С л е д с т в и е. Если f - непрерывна на [a, b], а на концах отрезка принимает значения переменных знаков (является знакопеременной), то $ точка х₀ Î [a,b]: f(x₀) = 0.

 

 

Дифференциальное исчисление функции одной переменной

Понятие производной

Рассмотрим задачу, которая приводит к понятию производной. Пусть функция u(t) выражает количество произведенной продукции за время t. Найдем производительность труда в момент t₀. За период от t₀ до t₀+∆ t количество продукции изменится от u(t₀) до u₀+∆ u = u(t₀+∆ t). Тогда средняя производительность труда за этот период z = ∆ u/∆ t, поэтому производительность труда в момент t₀

z = lim_{∆ t → 0}∆ u/ ∆ t.

Определение 1 (производная). Производной функции y = f(x) в фиксированной точке x называется предел

lim_{∆ x → 0}∆ y/ ∆ x

при условии существования этого предела.

Производная обозначается следующим образом f'(x) или y'.

Пример 1. Вычислить производную функции y = sin x. Найдем приращение функции:

∆ y = sin(x+ ∆ x)-sin x = 2sin(∆ x/ 2) cos (x+ ∆ x/ 2).

По определению производной

(sin x) ' = lim_{∆ x → 0}∆ y/ ∆ x

= lim_{∆ x → 0} (cos (x+ ∆ x/ 2)(sin ∆ x/ 2) / (∆ x/ 2)) = cos x,

так как

lim_{∆ x → 0}cos (x+ ∆ x/ 2) = cos x.

Таким образом,

(sin x) ' = cos x.

Определение 2. Правой (левой) производной называется правый (левый) предел

lim_{∆ x → 0+0}∆ y/ ∆ x

lim_{∆ x → 0-0}∆ y/ ∆ x,

если эти пределы существуют.

Для обозначения правой (левой) производной используют символ: f'(x+0) (f'(x-0)). Необходимым и достаточным условием существования производной является равенство f'(x+0) = f'(x-0).

Пример 2. Доказать, что f(x) = 3|x|+1 не имеет производной в точке x = 0. Составим ∆ y = 3(0+∆ x)+1-1=3∆ x при ∆ x>0. При ∆ x<0 ∆ y = -3(0+∆ x)+1-1=-3∆ x, значит,

lim_{∆ x → 0-0}∆ y/ ∆ x =- 3, lim_{∆ x → 0+0}∆ y/ ∆ x x = 3.

Поэтому данная функция не имеет производной в точке x = 0.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: