 |
Моделирование процесса разрушения
|
|
|
|
Металлических деталей
Модели развития трещин исходят из того, что в начальный момент на поверхности деталей есть трещины вследствие несовершенства структуры металла, дефектов изготовления, усталостных и коррозионных повреждений.
Развитие трещин, их распространение описаны аналитически. Условия распространения трещины эллиптической формы длинной при равномерном растяжении пластинки напряжением σ даны на основе закона сохранения энергии А.А. Грифитсом в 1920 году. Нестабильное состояние трещины (хрупкое разрушение) возникает при условии равенства изменения энергии напряженного состояния и изменение энергии на образование трещин [161]. В обоих случаях изменение энергии берется на единицу поверхности. При равномерном растяжении с напряжением σ величина изменения энергии на образование трещины зависит от площади трещины. Периметр трещины (рис. 2.12) можно принять равным 4l.С учетом величины энергии γ, приходящейся на единицу площади трещины, при единичной толщине пластины, величина изменения энергии составляет 4l γ.
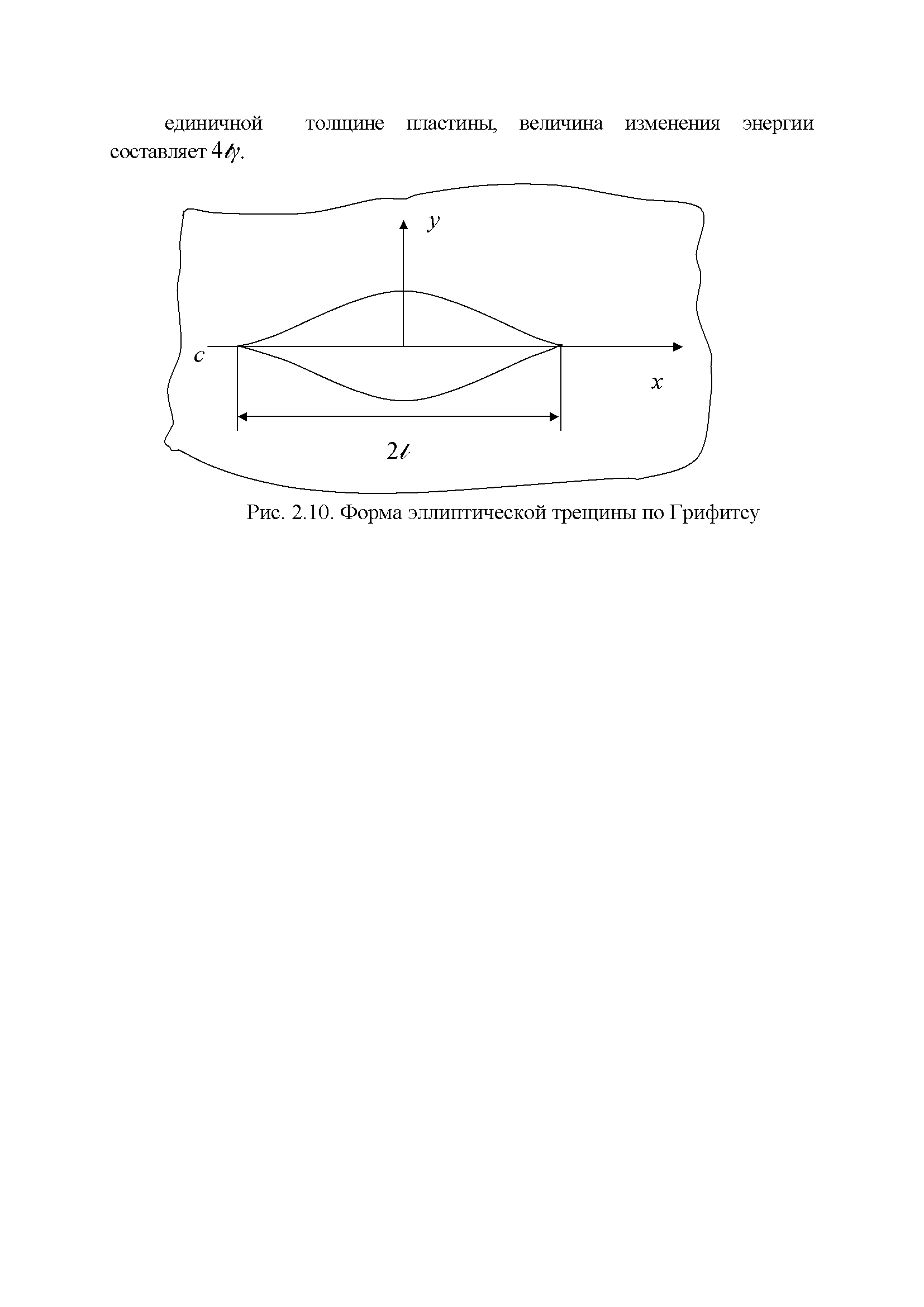
Рис. 2.12. Форма эллиптической трещины по А.А. Грифитсу
Величина энергии γ, приходящейся на единицу площади трещины в процессе ее развития, зависит от свойств материала и является его характеристикой (γ ≈ 0,01∙Е∙ r 0, где r 0 – межатомное расстояние). С возникновением трещины освобождается энергия (энергия раскроя трещины).
Изменение энергии напряженного состояния определяют как освободившуюся работу по обоим краям трещины (рис. 2.13). Численно освободившаяся энергия на единицу длины трещины при перемещении края трещины по оси у на Uу и при напряжении равномерного растяжения σ составляет σUу / 2.
|
|
|
Для заданных условий по данным теории упругости
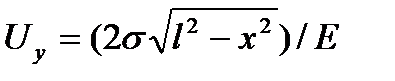. (2.8)
По всей толщине, по обоим краям величина освободившейся работы
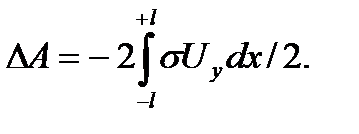(2.9)
Или с учетом приведенного значения Uу
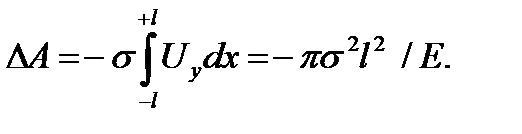(2.10)
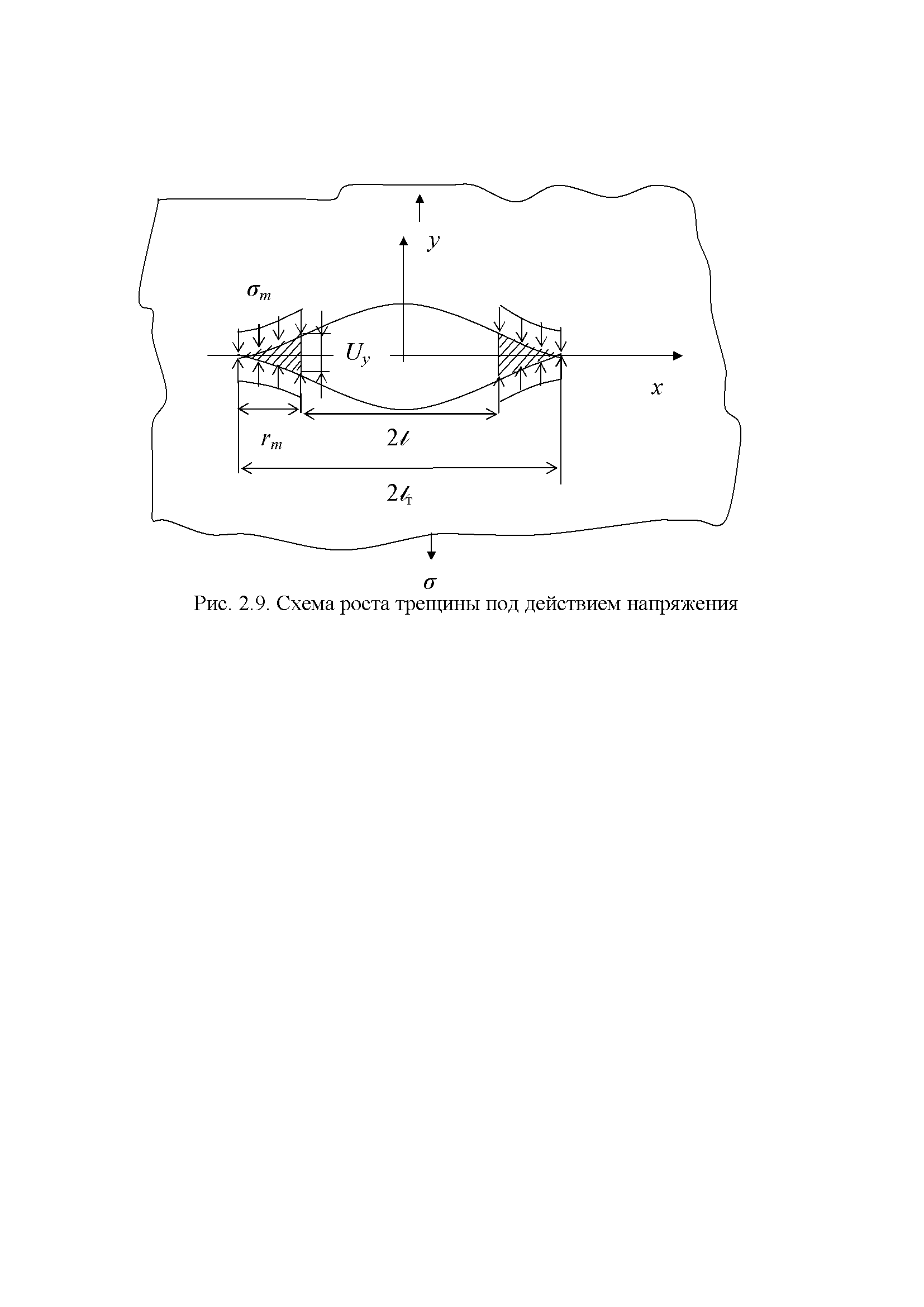
Рис. 2.13. Схема роста трещины под действием напряжения
Если при дальнейшем росте трещины добавочно освобождается энергия меньше необходимой для дальнейшего развития трещины (меньше работы, потребной для преодоления сил межмолекулярных связей), то разрушения не будет, трещина не распространяется.
По мере увеличения трещины уменьшается энергия напряженного состояния, увеличивается энергия на развитие трещины. Максимум алгебраической суммы этих энергий определяется из условия
(2.11)
После достижения этого максимума (рис. 2.14) трещина увеличивается без подвода энергии извне, развивается за счет расхода потенциальной энергии упругой деформации пластины, возникает хрупкое разрушение.
При этом напряжение σ и длинаl распространяющейся трещины связаны зависимостью
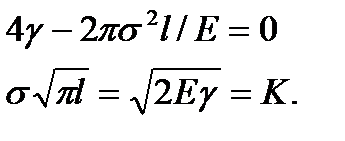(2.12)
Выражение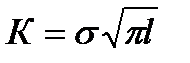 
характеризует коэффициент интенсивности напряжений, критическое значение которого
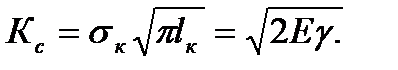(2.13)
при критических величинах σк иlк. С практической точки зрения очень важно знать величину σк (при котором наступает быстрое разрушение)
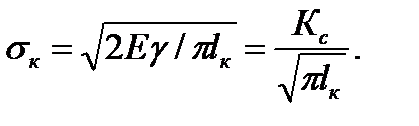(2.14)
| σ A |
| 4l γ |
|
| l |
| σк |
Рис. 2.14. Зависимость энергии раскрытия трещины от ее длины
В дальнейшем происходит распространение трещины с пластической деформацией в тонком слое около поверхности трещины. Энергия γр, образование которой существенно превышает энергию γ разрушения при упругой деформации. Поэтому для металлов суммарная энергия на образование местной пластической деформации γр и разрушение γ мало отличается от энергии γр (то есть, γк=γр+γ≈ γр). Из этих условий напряжение σк, при котором трещина начинает распространяться, составляет
(2.15)
|
|
|
Энергия пластической деформации приближенно оценивается как работа статического растяжения до предела прочности σв и удлинения lb (в пределах равномерного деформирования гладкого образца) в слое толщиной Δ по нормали к поверхности трещины. Эту работу по предложению Я.Немец можно оценить по формуле [161]
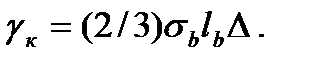(2.16)
Величина Δ измеряется металлофизическими измерениями (в том числе и рентгеноструктурными) и составляет для малоуглеродистых сталей 0,1 – 0,5мм.
При известной величине энергетического критерия разрушения γ к из предыдущей формулы можно оценить критическое значение коэффициента интенсивности напряжений в условиях возникновения неустойчивого состояния трещины
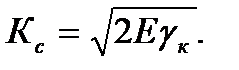(2.17)
Таким образом, величины Кс и γ к являются характеристиками сопротивления материала возникновению хрупкого разрушения при наличии исходной трещины. При заданной длине трещины величину напряжения можно увеличить до критического значения
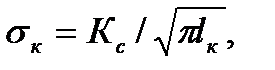(2.18)
при котором произойдет неустойчивое, спонтанное развитие трещин, и тело разрушится.
Если на пути трещины препятствие, то может происходить устойчивое развитие трещины, без окончательного разрушения тела в значительном диапазоне изменения нагрузки. В конструкциях, работающих при определенных внешних нагрузках наличие устойчивых трещин не опасно. Срок службы их можно значительно продлить, искусственно, усиливая их заклепками и пластинами, высверливая отверстия на пути распространения трещин и т.д.
|
|
|
